１. 名月をとらえる

      「名月をとってくれろと泣く子かな」という句がありますね。いま少女が三 日月を捕らえようとしています。むろん、こんなことは不可能ですが。月と少 女を重ねてみると、月が彼女の手中にあるようです。

        左の名月をとらえてみましょう。像 を得るだけならカメラで写せばよいわけ ですが、距離の情報も含めたものにした い。
明るい街灯の下から満月をながめたとき を想うと、月と街灯を交換することができればよいわけです ね。それが可能なら、いっそのこと全宇宙を机上に載せること を考えましょう。
         まてよ、宇宙といえば広大無辺ではないか。無限の彼 方に印しを付けることはできません。紙に線を引いて、その端 を無限の彼方だと決めつけることもできません。その印しを付 けたところより先きがあるのですから。

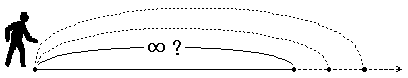
それでは、どうすれば私たちは無限の果てをつかむことができるのでしょうか？

２．無限の果てをつかむ

      無限に遠いところ無限遠を私たちの目に見える有限のところへもってくることを考えましょう。

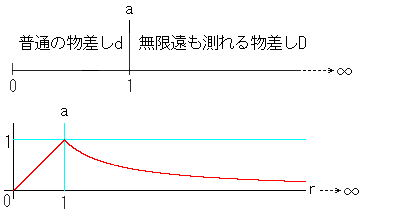
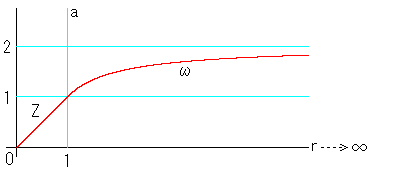
一つの方法は、私たちがある領域内にいるとして、その内側と外側で物差し を換えるのです。その境界aを便宜上1とすると、無限遠も測れる物差しは、 普通の物差しで距離dのところをDとして

                        D = 1/d　(d≧1)

の関係にあるようにします。つまり、d → ∞ のところが D → 0 という私たち の視界内にくるのす。グラフでは図のようになっています。Dのカーブは直角 双曲線の一枝です。aはdとDの境界で、rは原点Oからの普通に測った距離 です。しばらくは、距離をdで測るところをZ平面、Dで測るところをω(オメガ)平 面とよぶことにします。

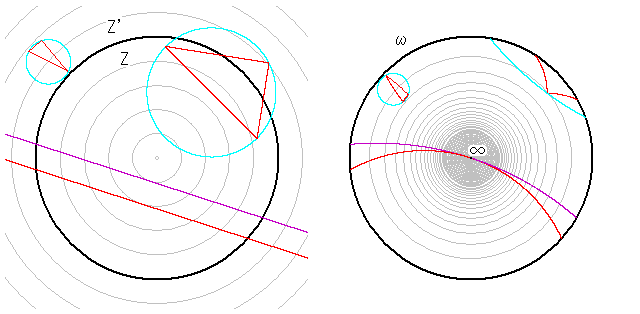
       ω平面はＺ平面にかぶさっています。こんな風にする のを反転というのですが、そのままだと見にくいので、分け て描きました。Ｚ'は境界aより外側です。２つの直角三角形と 平行線です。水色の円は三角形の外接円で、三角形の内 角はＺとωで変わりはありせん。いわゆる等角写像になって います。ω領域では、平行な２直線が無限遠∞の1点で出 合っています。

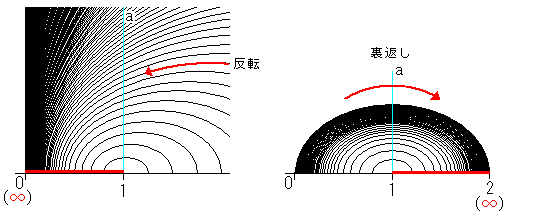
       すべての無限遠が1点になるというのは、不合理でないに しても、なじみにくいですね。そこで、Ｚ平面の上にかさなってい るω平面を境界aを軸に裏返してみます。そうしてできた 平面をかりにＺ+ω平面と名付けておきましょう。

グラフで見ると折れ線にならず、どこも滑らかです。ここで“滑らか”といってい るのは、目で見てそうだからです。数学的に厳密なものでないた めに、Ｚとωをつらねた全体を１つの式で表すことはできません。ともかく様子を見てみましょう。

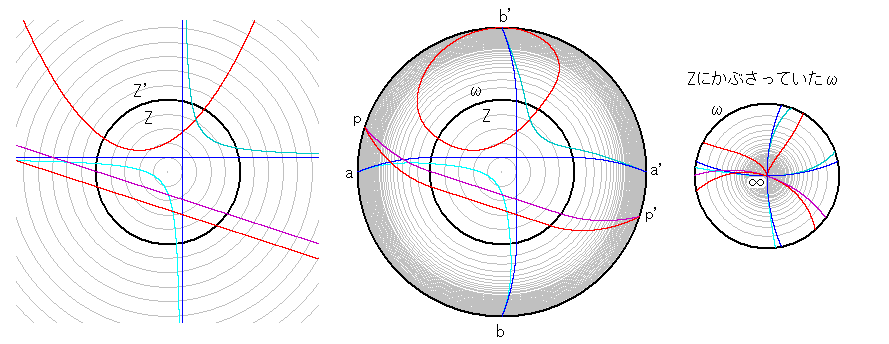
平面Ｚからそのまま無限に 広がった平面Ｚ'へと伸び ている放物線と双曲線と 平行線を描いて、Ｚ+ω平 面に写します。そこでは、 放物線がループになって います。しかし、双曲線は そうは見えません。けれど も、Ｚ平面にかぶさってい たω平面を見ると、点aと a’、点bとb’をそれぞれ同 一視すべきです。つまり、 双曲線は a−b−b'−a'−a とループになっているので す。平行線も同様です。

       これで無限の彼方を手もとへ引き寄せることができました。けれどもヘンな具合ですね。無限 に曲線を延ばすとループになるだとか、同一視がしいられるとは、すんなりと受け入れるには何か 抵抗を感じませんか。それに、途中で物差しを代えるだとか。原点からの直線距離rについては、 それでも我慢できますが、円周方向の物差しはどうなるのでしょうか？　各点ではどんな分度器が 通用するのでしょうか？

３．もう一工夫

      半径方向だけですが、１つの物差しで測れるようにします。

グラフで見るように直角双曲線の１枝をつかいます。Rはω平面上の半径 方向の作図距離です。ｒとＲの関係は、

                        R = r / (r + 1)
です。

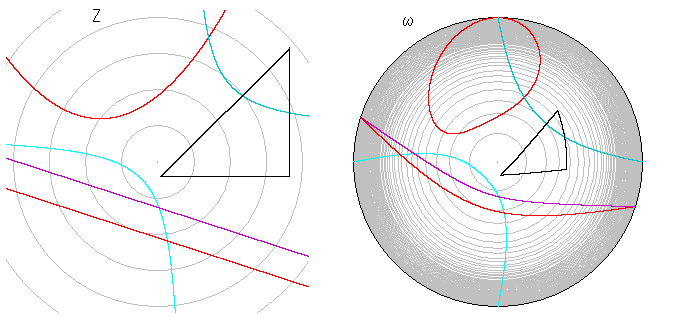
左図は、こうしたω平面へ、Ｚ平面に描いた放物 線、直角双曲線、平行線、直角二等辺三角形を 写したものです。ω平面上では、点の原点からの 距離rは、図上でふつうの物差しで測ってRのとこ ろが
                        r = R/(1-R)

となっていて、R →１のとき r → ∞ になります。 ω平面の黒い外周は半径 R = 1 で描かれていま すが、式の分母を見てもわかるようにRを1にとる ことはできません。したがって、rはいくらでも大き くはなりますが、無限遠という終点が仮にあるとし ても、そこへ到着することはけっしてないのです。ドアーは閉められていないけれど、部屋から出ら れないといった感じです。数学でいう開領域です。

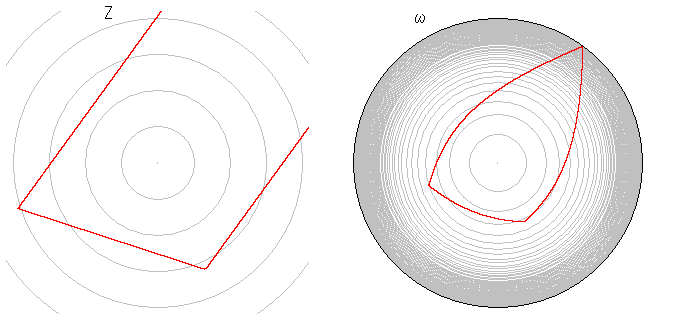
       頂点の１つが無限遠へ飛び去っている三 角形は、その頂点をはさむ２辺が平行です。そ してω平面では図のように砲弾型に見えます。 むろん、それは私たちから見てのことであって、 ω平面の住人にとっては、そうではないはずで す。長さが無限大の辺の比なんて、考えようが ありません。となると、円周率πが定数だという ことも怪しくなってきました。三角形の辺の比が きまらないようなところでは、当然ピタゴラスの 定理が成り立ちません。一体それはどんな世 界でしょうか？　物差しとどんな関係あるのでし ょうか。

４．タテもヨコも測りたい

       ω平面のようなものの中でどんな方向の長さも測れるようにしたい。それは比で測るというも のです。

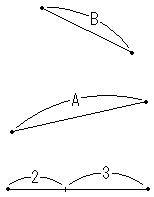
場所によって伸縮している平面上に２つの線分があります。その長さA,Bは異なるように見えます が、実際は同じ長さ A = B であって、線分が平面とともに伸縮しているのです。同じ長さであること を示したいのですが、平面の伸縮とともに伸縮をする物差しがどこに在るのかわからないのです。 どうしたらよいでしょうか。
ひとつの方法として、長さを比で表わすのです。たとえば、Aの長さを“2：3”だと表現しBも“2：3”だ といえば、A = B を指していることになります。“2：3”っていくらだと問われたら、2/3とか3/2と答え ることにします。この考えを私たちのω平面に利用しましょう。

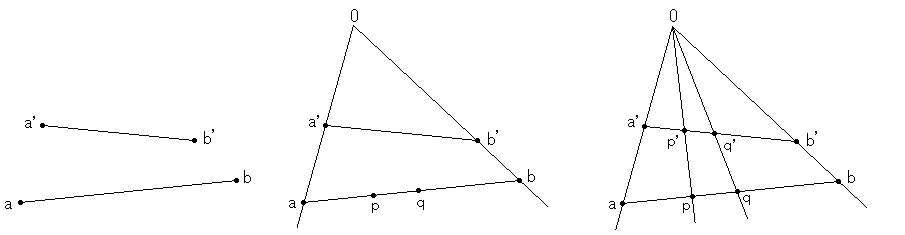
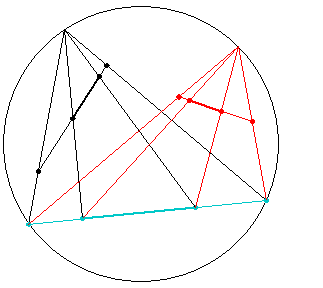
ω平面上に同じ長さの 線分abとa'b'がありま す。線分a'b'は線分abが 移動したものです。その a,a'を通る直線とb,b'を通 る直線との交点Oを得ま す。そして、線分ab上に 2点p,qをとり、交点Oから 点p,qへ向けて直線を引 き交点p',q'を得ます。こうすることで点pや点qに対応する点p',q'が定まって、長さpqとp'q'が等しいこ とがいえるようになります。

      具体的には、比の比である複比というものをつかいます。それは比とよばれていますが比の 値のことで、よくλ（ラムダ）で表されています。少なくも3つは異なる4つの数S,P,Q,Tから

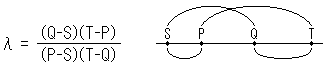
としたものを用います。この計算は、X座標かY座標のいずれか一方だけででき ます。
すると、図の3つの太い線分の長さが等しいということになります。し かし、等しいことはいえても、長さとしての足し算ひき算ができるのでしょうか。

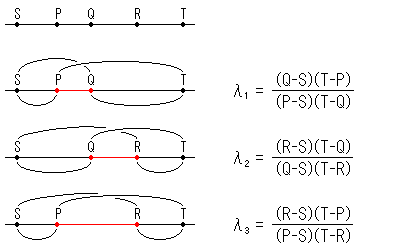
直線上に5つの点S,P,Q,R,Tをな らべます。そこから4つとって上と 同じタイプの複比をつくり ます。そのは長さPQに、は 長さQRに、は長さPRにそれぞ れ対応しています。そして、

               

の関係になっています。これは掛け算ですから、長さの関係である足し算の形に直すために両 辺の対数をとると、

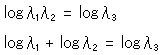
うまく足し算の形になりました。そこで、

と約束（定義）することにします。むろん、長さとか距離というときには、必要に応 じて絶対値をとらなければなりません。kは長さの単位を合わせる定数で、1か 1/2にとるのがふつうです。対数は掛け算を足し算に変える唯一のものです。対 数の底は1より大なら何でもよいのですが、都合のよい自然対数の底eにしてお きます。
       これで円内がω平面の世界であるときに、そこでのタテもヨコもどの方向の 長さもいえるようになりました。

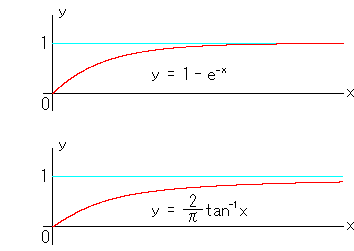
       早速、試してみましょう。イヤ、まてよ。ここに対数が出てきたことに注目され ますね。「３. もう一工夫」のグラフの曲線に似たものに右上のような指数関数の 曲線があります。xは原点からの距離で、yはそれをω平面上に変換したものです。対数の記号log で式を書けば、x = -log(1-y),　y < 1 です。似たものなら、馴染みのあるtanのカーブもその一つで す。こんな風に似たカーブのものがいくらでもあるとすると、試すにしても、もっとも好ましい曲線を 見出したうえで行うべきですね。まずは、その曲線を探しましょう。

５．無限遠を引き込むさらなる手

       これまでは変換式を作って Z→ω としました。ここでは、無限遠を有限のところへ引き込むの に回転曲面を利用します。

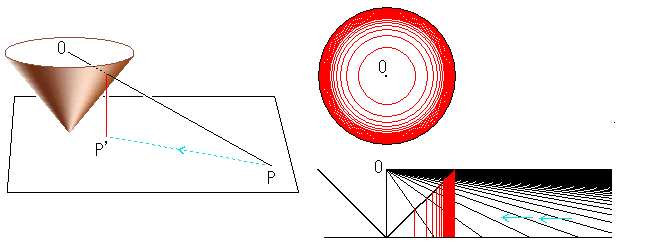
まずは円錐を使ってみます。
円錐を逆さにして頂点を平面に立て ます。平面上の点Pから円錐の底面 の中心Oへ射線を引きます。射線が 円錐の側面を貫通するところから赤 い線のように平面へ向け垂線を落 します。その垂線が平面に達した 点P'が、点Pを円錐のそばへ引き寄 せたところです。平面が無限に広く て、点Pが無限遠にあっても同様で す。

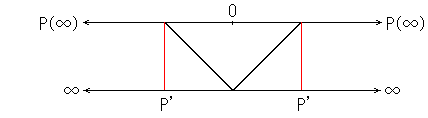
むろん無限遠に在る点Pと手元の中心Oを実際に線でむすぶこ とはできませんが、点Pの方角は指すことがでるはずです。“は ず”といったのは、前に見たように、無限遠というものは前方と 後方を同一視して捉えるべきものだからです。それなら、描いた 射線の図の点Pは、いくらでも遠いところのものでもよいが、無 限遠ではないとします。そして、無限遠を組み入れた図を右に掲げます。
今後、特殊な場合以外はこのような図は省きますが、無限遠を含めればこんな風になることを覚 えておいてください。

       ところで、この円錐は底面の半径は1に、母線の傾きを45°にとってあるので、変換式は
R = r / (r + 1) です。なんのことはない、「３. もう一工夫」のとまったく同じです。

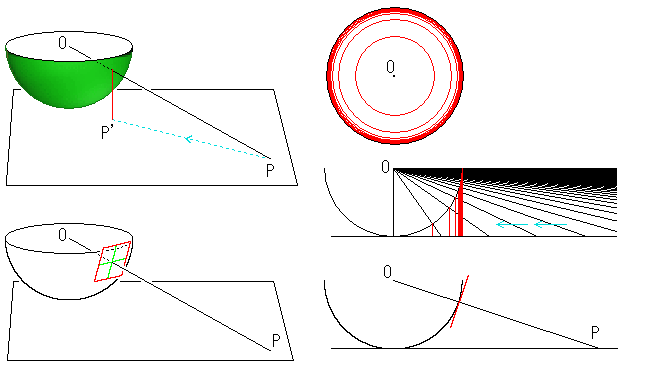
これから先、ω平面としての 半径1の円をω円板とよぶこ とにします。図では真上から 見たときの赤い同心円が描い てありますが、それはω円板 に描かれたものと理解してくだ さい。

        半球ではどうでしょうか。 なんだか、この方が好いよう な気がします。それは、中心O から点Pを見たとき、射線OP が通るところの半球面の接平 面が真正面にくるからです。カ メラのファインダーと同じです。

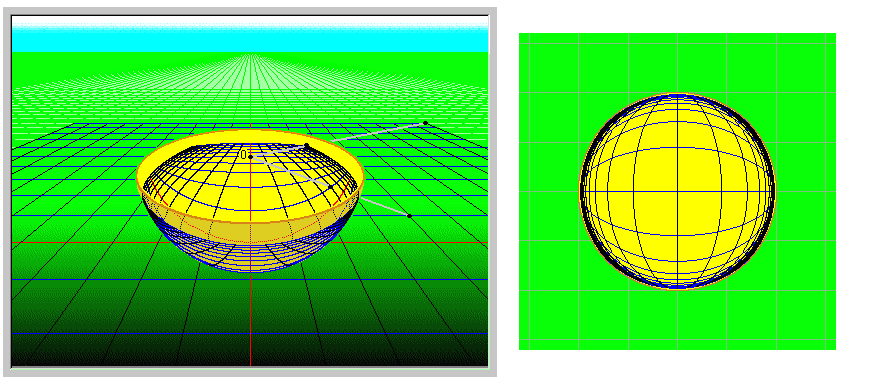
        この半球面を利用したと き図形がどうなるかを見てお きましょう。
平坦な無限に広い原野に格 子パターンが描かれてあるの を半球面で射影したもので す。向こうの方に青空が見 えています。真上からの図は、半球面の内側とその下の平 面に射影されたものが重なっ て見えています。

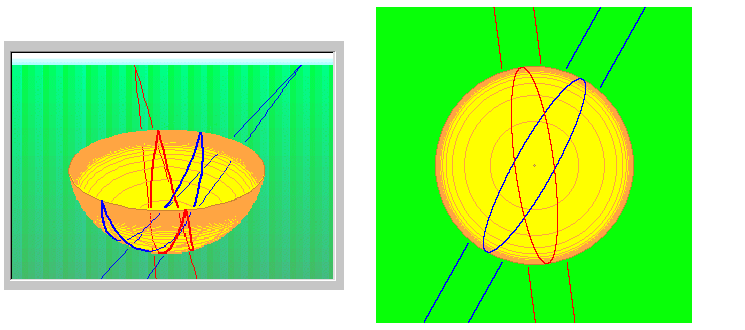
２組の平行線です。
真上から見た図では、ル ープになった平行線の先 端が尖っていません。全 体がまるく楕円になって います。

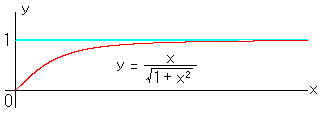
変換式のグラフを添えておきます。ルート√が現れていますね。


       半球をすこし変えて椀（わん）状にしました。何がどう変わるでしょうか。

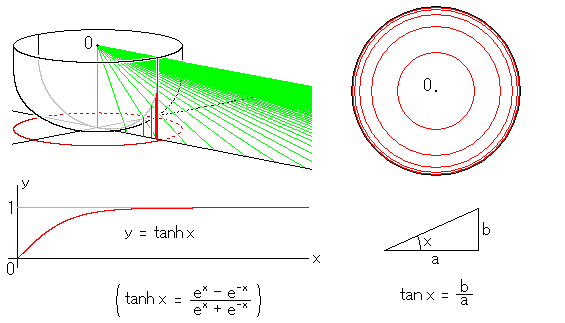
椀の下の円は、真上から見たときの椀の影、つま り椀の正射影です。十字の直線は平面を表現す るために添えた直交軸です。変換式は、グラフの 下のカッコ書きのように自然対数の底eをつかった ものです。tanh（ハイパー ボリックタンジェント） は、ふつうのtanとよく似た性質をもっています。
sinh（ハイパーボリックサイン）、cosh（ハイパーボ リックコサイン）もあって、これらは双曲線関数と よばれています。
tanhの定義式には4つもeがあって、ややこしそう ですね。でも、ふつうのtanのほうには不便なとこ ろがあるのです。というのは、tanh x はｘ一つだけ で決まりまるのに、tanの定義式を見ると右辺には xがありませんし、tan x のxは角なので X = 90° などとすると発散してしまいます。そのうえ、tan x の値はぐるぐると同じになります。一方、tanh x のxは角ではなくて、値の制限もありません。そん なわけで、そのうちにtanhとも仲良くなれます。（付録参照）

       椀の作図のタネを明かすと、この椀は初めに与えたものではありません。わざと y = tanh x
に合った形になるようにしたものです。それはまず、平面上に椀の下端を通る直線Aを等間隔に細 かくキザんで、適当な高さをとった中心Oから緑色の射線群を引いておきます。そして、同じ直線A 上で、そのxに対応するyの値のところに赤い垂線群を立てます。つぎに、椀の下端から順に赤と 緑の交点を結んでいくと椀状の曲線が得られます。

６．アイスクリームがもらえる

       tanh x をつかったので、こんどはそのxを半分にして、y = tanh x/2 で変換 します。

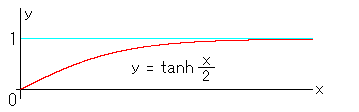
半分にするだけですので、どうなるか予想してみてくだ さい。ヒントは右の写真です。変換式のグラフを見る と、かなりなだらかになっています。

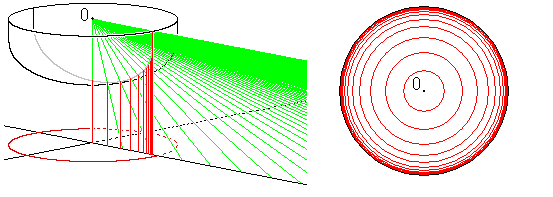
前回と同じ要領で射影図を描 きました。なんと、椀が浮き上 がっているではありません か。これにスタンドを付ければ、写真と同じアイス クリームグラスになります。そして、ω円板上の 同心円が中心寄りになっています。

７．動かす

       ω円板上で2つの線分が与えられたとき、それぞれの長さをいうことはできます。また、1つの 線分が与えられているときに、それと同じ長さの線分を別の場所に引くことも作図的にすぐにでき ます。しかし、ある図形をそっくり移動するのを作図的にやるのは困難です。移動中の様子を見る ときには、途中ずっと長さが保たれていなければなりません。ですから、「どの方向の長さもいえる ようになったので、それを試してみよう」といいましたが、その前に等長変換(長さを保つ動かし方） について知らねばなりません。

       ふつうの日常生活で、ものが勝手に伸びたり縮んだりすつことは、めったにありません。ω円 板上の住人にとっても、それは同じです。彼らがものに合わせて伸縮する物差しをもっているわけ でもありません。彼らにとって、大地は広大無辺なふつうの平面です。ところが、ω円板の外いる 私たちには、そこのものの長さが伸縮して見えます。そこで、ω円板上の住人にとっても、私たち にとっても、同じものは同じ長さとして測れるようにしておかねばなりません。それが等長変換とい うものです。いま一つピンとこないと思われても、そのまま読みすすんでください。わだかまりは、 間もなく消えます。

       ω円板上で等長変換をするには、どうすればよいでしょうか。すでに見たように、複比というも のが変わらなければ長さは変わりません。つまり、等長変換とは複比を保ちながら動かすことで す。そんな巧い動かし方があるのでしょうか。

       点P(x,y)をP(x',y')へ動かします。それには、たとえば一次変換

でもよいですね。動かすだけなら、むろん2次式や3次式とか三角関数や指数関数などでカーブを つけて動かしてもかまいません。しかし、等長変換となるものとしては、上の式に名前も姿も似て いる一次分数変換

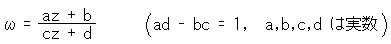
をつかいます。一次分数変換をたんに一次変換という人もいるので、混乱しないでください。ここ で、ωとzは複素数です。（複素数に馴染みのない方や、もうすこし一次分数変換について知りた い方は、付録をめくってください）
実際に図形を描くために、実数だけの式に直します。

と表すと、一次分数変換の成分は

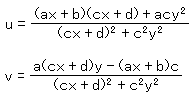
となります。a,b,c,d をどうとるかは、目的地やコースによります。
これでω円板上で図形を、その各部の長さを変えないで動かせるようになりました。それでは、動 かしてみましょう。

８．モデル出現

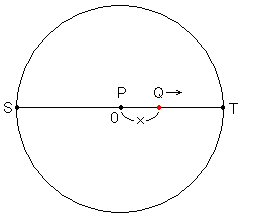
       一次分数変換で

                                  a = d = 1, b = c = 0

にとると、u = x, v = y となります。そして複比のS,P,Q,Tを

                                  S = -1, P = 0（原点）, T = 1

に固定して、Qを変数xに置き換えます。すると複比λは

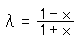
であって、長さPQをDと表すと

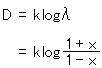
となります。このDがω円板上の住人が知ることのできる距離です。そして、ω円板の外にいる私 たちがふつうの物差しで測るのがxです。
こうしておいて、k =1 にとり、y = 0 としてxを0（原点）から動かします。すると、

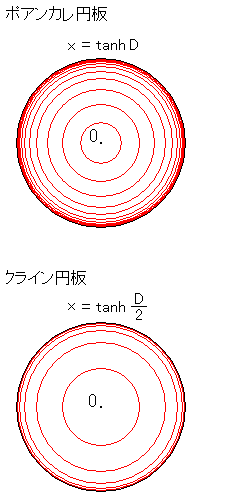
となります。
       xをDで表すと、x = tanh D/2 と書けます。このDを等間隔にキザんで、ω円板に描くと左 上の図のようになります。そうです。これはアイスクリームグラスのときのものと同じです。そ れでは、半球に似た椀での変換式もDをつかったものに改めてみましよう。それは簡単で、
k = 1/2 にとって文字を入れ替えればよいだけです。

       この二つの円板には図のように名前がついています。あの怪しげな双曲幾何のモデルといわれているものです。
いや、怪しげなのは、むしろ私たちの方こそではないでしょうか？ ちょっと振り返ってみましょ う。複比と対数と双曲線関数という3つの武器をつかった。そして、ω平面の世界とその外側 に立っている私たちとの幾何学的な関係を探ってきた。3つの武器のうち、双曲線関数だけ が天下り的に取り入れられた感じがする。しかし、ふつうの三角関数のように双曲線関数に なじんでいたとしてら、手元にあった関数をつかっただけのことになり、不自然さはなくなる。 それは認めることにしよう。それにしても、なぜ、指数関数や三角関数からなる変換式を見捨 てたのか。それらが不適格であるなら、それを明らかにしておくべきである。

       そういわれてみると、たしかにそうですね。たんなる予感だけで避けるのはよくありませ ん。あとで再考します。ともかくいまは前へ進みましょう。そうすれば、その明らかにすること も、たやすくなりそうです。

       さて、双曲幾何のモデルが2つも出てきました。どちらも円板です。そして、ともに正しい といわれています。どうなっているのでしょうか。

９．ゆがんだ世界地図

       私たちは、地球に住んでいます。それが球形だということは知っていま すが、宇宙飛行でもしないかぎり自分の目で確かめることはできません。し かし、宇宙飛行のテレビを見たり、地球儀をながめると、実感したような気が します。
世界地図を作るメルカトール図法です。まず、巨大な地球を紙の上に描くた めに、地球を小さく見立てます。そして、地球上の点を巻きつけた紙に射影し ます。縮尺が高緯度になるほど小さくなっているので、あまり高緯度のところ は描けません。でも、この地図はとても役にたちます。それは、どう歪んでい るかを私たちが知っているからです。
どうしたことか、小中学校では、この絵の図法で世界地図がつくられていると 教えています。本当のメルカトール地図は、等角写像というものに基づいて います。メルカトールさんは微分も積分も発明される前の1569年にそれをし たのです。一体どうやっのでしょうか。ともかく、図は正しくないのですが、こ こでは簡単のために使っておきます。

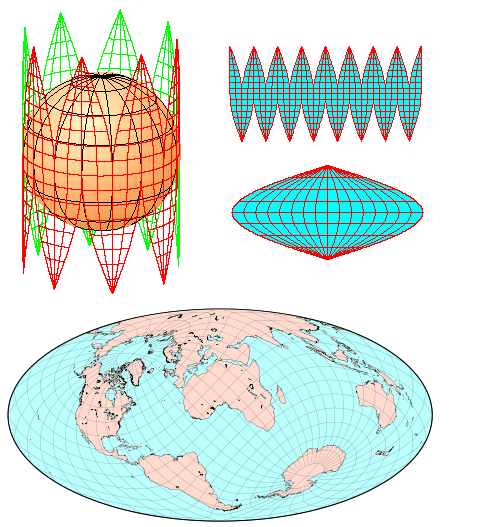
       円筒の中の小さな地球の地軸を円筒の軸にあわせたメル カトールの世界地図には北極も南極もありません。リンゴの皮 をむくようにして球面を平面に近づければ、北極も南極も含める ことができます。しかし裂いたままでは見にくいので、そこを1点 にしぼります。南北両極が尖っていて不自然ですね。
南北両極もよく見えて全世界をまるく描いたものもありますが、 ひねられていて、緯線がS字形になっています。
インターネットにもいろいろな世界地図があります。
どの世界地図でも、小さな部分を見ているときは、ほとんど歪みをかんじません。しかし全体を見ようとするとき、実際は上下左　 右のつながったものだと想って捉えるのはしんどいですね。

       地図は、どんなに歪んでいても、距離や角を定められたル　 ールで測ることにすれば、100％正しいといえます。長さを細か　 く測るルールを計量といいます。 ピタゴラスの定理とのちがいを　 表わしているものです。
       それでは双曲幾何の世界の地図は、どんなのでしようか。
それはモデルとよばれていて、ユークリッド幾何の世界に住む 私したちが見ることのできるものです。ふつうモデルというとき、 目に見える実物を縮小した模型のようなものを指します。ところ 双曲幾何のが、双曲幾何の世界というのは存在するのは確か なのに、私たちが見ることはできないのです。実物を縮小した模 型もありません。これが、双曲幾何が疑われる最大の根拠です。けれども、ありがたいことに、双 曲幾何のモデルは理論的に実物と完全に一致しています。ですから、モデル上での様子を見れ ば、双曲幾何の真の世界の様子を知ることができるのです。
       それは、わかった。しかし、モデルを通して実体を知るというのには、相当な想像力を駆使し なければならないことも事実です。そして、その想像が正しいかどうかも考えねばなりません。しか し、ことは馴れではないでしょうか。勇気を出して、モデルに頼っていきましょう。

１０．イチョウの葉

      双曲幾何の世界、「双曲世界」は一つしかありません。それなのに、ポアンカレ円板とクライ ン円板という同じ円形のモデルが現れました。どこが違うのでしょうか。

      まず、“ことば”を整えます。
「双曲界」･･･ 双曲幾何が成り立つ世界
「双曲界人」･･･ モデル上を含む双曲界の住人
「双曲距離」･･･ 双曲界人が知ることのできる距離
「ユークリッド界」･･･ ユークリッド幾何が成り立つ世界
「ユークリッド人」･･･ ユークリッド界にいる私たち自身を含めた人々
「ユークリッド距離」･･･ ユークリッド人が知ることのできる距離
「無限遠円周」･･･ モデル円板の円周
「r方向」･･･ 原点から見た方向
「θ方向」･･･ r方向に直交する方向

      さて、2つのモデルの差異を探っていきましょう。
モデル円板に原点中心の同心円を描いただけではθ方向の様子がわかりません。

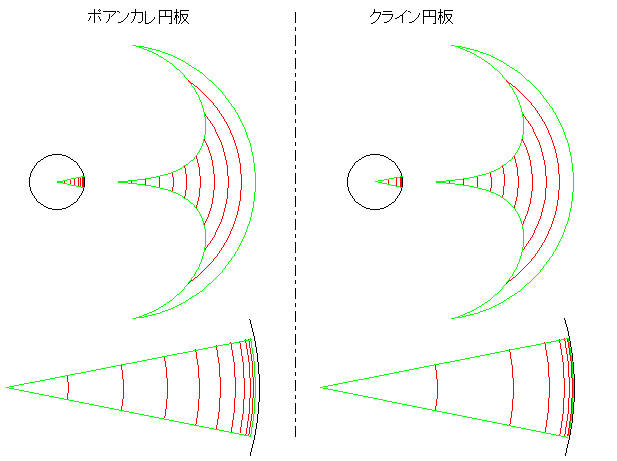
      図の小さな円はモデル円板です。θ方向の双 曲距離をありのままに描くために、モデル円板から 無限遠円周を含めない扇形を切り出します。そし て、原点からの双曲距離を等間隔にキザんで伸ば していきます。すると、それにつれてθ方向の双曲 距離も伸びて扇形が押し広げられていき、イチョウ の葉のようになります。右の写真によく似ています ね。
押し広げられるのは、

        θ方向の双曲的長さ = θsinh r
        (r = 双曲半径, θ= 扇形の中心角)

という関係があるからです。θはユークリッド角と 同じです。（付録参照）
      図のイチョウの葉のようなのは、モデル円板 と同じ尺度（スケール）で描いたものです。いか にモデル内での双曲距離が無限遠円周に近づく と急激に増大するのがわかります。

大きな扇形は、モデル円板のところにあるのを拡大したものです。黒い円弧は無限遠円周の一部 です。扇形内の赤い同心円弧は、どちらも同じ双曲距離を0.5ずつでキザんだものですが、そのパ ターンは明らかに異なっています。そのため、変換式の違いによってモデル円板上に描かれる図 形の姿は、見た目に大きく変わります。ところが図の2つのイチョウの葉はまったく同じです。2つ のモデルは、双曲距離とユークリッド距離の変換式が違うだけで、本質的には差異のないもので す。
       それでは、なにがモデル円板を双曲界として成り立たせているのでしょうか？
これまでに手にした数冊の本のすべてが、私には、とつぜん天下り的にモデルを出していると感じ ています。天下りにモデルを用いるなら、そのことを明かせばよいのにと不満です。彼ら著者たち は、そのモデルが設定した公理を満たすことについては熱心に説いています。でも、話の順がお かしいですね。かくかくこういうわけで、このようにモデルが構成されるのだと説明してくれればあり がたいのに。と、思えてなりません。
       「それじゃあ、お前がそれをすればよいのだ」といわれると、はてさて、どうしたものでしょう か。

１１．モデルの生まれ

       双曲幾何のモデルはどのようにして生まれたのでしょうか。

最初の円板モデルはクラインという人がつくったのですが、彼がそれまでに得ていた情報は：
       1826年2月11日、ロバチェフスキーが新しい平行線公理から双曲幾何を発見し、その三角法        を証明した。
       その前後に：
       複素数がかなり普及していた。
       ランバートが「ユークリッドの平行線公理を否定した幾何は、虚球面（半径が虚数の球面）上        の幾何だ」といってい
       ポンスレーが射影幾何をつくり、無限遠をあやつっていた。
       ケーリーが射影幾何での計量（射影計量）を見出していた。
       ベルトラミーが、双曲幾何は擬球とよばれる曲率が負で一定の曲面であることを示していた。        （右のラッパのような絵が擬球で、双曲幾何の平面（双曲平面）の一部です。）
といったことです。
クラインは、射影計量と双曲幾何との関係からモデルはこうなるのでないかと試作しました。そし て、それが双曲平面であることのすべての条件を満たすことを確かめました。そのことは、双曲幾 何が幾何として完全なものであることも認められる根拠ともなりました。

       さて、クラインはどのように円板モデルを構成したのでしょうか。現代の本を見ると、なんのい われも語らずに、式のなかの虚数記号をむしり取ったり、プラス（+）をマイナス（-）に換えたりし て、双曲幾何の話へとすすんでいます。想像するに、クラインもそうしたはずです。つまり、推論を ジャンプさせて結果がうまくいったのだから、そのジャンプは正しい推論の過程でありテクニックの 一つであると考えます。そう考えれば、推論に切れ目はありません。

       私たちは、これを受け入れることにします。その上で、ロバチェフスキーが創造したことから辿ってみましょう。

１２．平行線は交わるか

       素朴に、交わらないのを平行線といいます。そして、どこまでも伸びているものを想像します。 これを疑った人が昔から沢山いました。しかし、誰も疑わしいこと自体すら明らかにすることができ ませんでした。それでも、1697年になってサッケリーが双曲幾何のいくつかの定理を発見しまし た。（彼自身は自分の証明を信じませんでした。）1750年代には双曲線関数が見出されています。 機は熟してきました。1826年ついに、ロバチェフスキーが双曲幾何をつくりました。

       ロバチェフスキーは、平行線とは無限の彼方で交わるものだと仮定しました。どのように考え たのでしようか。 私たちなりに理解してみましよう。

       ユークリッドの原論から平行線に直接関連して注目されるものを挙げますと、
            定義23： 平行線とは、同じ平面上の2直線であって、両方向にいくら伸しても、そのどちら                          の側においても交わらないものである。
            公準1： 2点をむすぶ直線は、1本あって、1本に限る。
            公準2： 直線は、いくらでも伸ばすことができる。
            公準5： 1直線が他の2直線を切っている。その2直線を十分伸ばす。すると、その2直線                            は、内角の和が2直角より小さい側で交わる。

ユークリッドのいう“直線”は有限な線分のことです。どれも、当たり前のことをいっているようです が、ことを事前にこんなふうに不動の約束として決めて（仮定して）おかないと、論理が崩れるから です。

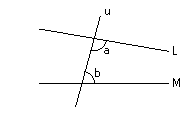
       私たちの公準5の理解は右図において、u,L,Mは有限な直線です。もし a + b < π ならば、 直線LとMはa,bの側で交わるというものです。
ユークリッドは、特定の場合 a = b = π/2 や a + b = π については、交わるとも交わらないとも 言っていません。“いくらでも”とか“十分に”とはいっていますが、“無限に”とはいっていませ ん。なんと巧妙に、彼は無限を避けているではありませんか！

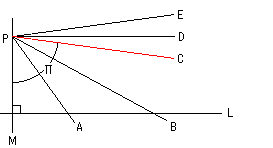
       さて、ロバチェフスキーのアイデアのキーポイントを見てみましょう。
直線Lを引き、その上にない点Pをとります。直線PMは直線Lに垂直です。 点Pから 放射状に直線A, B, C,,,をひきます。赤い直線Cから下の直線A, Bなどは、直線Lを切 ります。赤い直線Cから上の直線D, Eなどは、いくら延長しても垂線PMから右側で直 線Lと交わりません。赤い直線Cは特別で、直線Lと交わるのか交わらないのかわか りません。そんな直線Cが存在するとして、直線Cは直線Lに関して平行であるといい ます。そんな直線Cがあると仮定することは、はっきりとユークリッドの平行線公理 （公準5）を否定しているわけです。
そうして彼は、角（パイ）を平行角と名づけました。

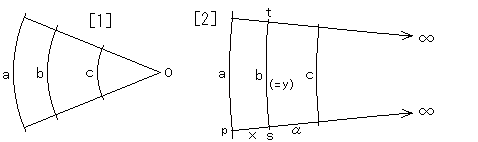
       a,b,cはユークリッド幾何での長さです。[1]の a,b,cの間隔を維持したままで、中心Oを無限遠へ 追いやりると、[2]のようになります。このとき、上 下の半径はユークリッド幾何でいう平行になって いるのかどうかわからないと考えます。そうする と、a,b,cの大きさが等しくなっているとはいい切れ ません。そこで、a,bの比はxの関数であるとする と、

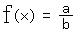
と書けます。このxの関数f(x)を求めましょう。

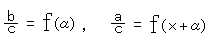
であり、

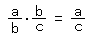
ですから、

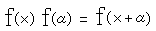
となります。したがって、ここで掛け算を足し算にするには対数(log)でというのを思い出せば、

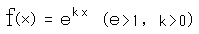
と解が得られます。この結果をつかって確かめるのは簡単です。

       こう掴んでおいて、簡単のために、    a = 1    k = 1    e = 自然対数の底にとります。b,cは、
a = 1 に応じた値になります。 kは長さの単位に拠る定数です。

bを変数yに書き換えると、  a/b = f(x) から 1/y = f(x) ですので、

を得ます。
この式(*)が、革命的な ロバチェフスキーの出発点です。

そして彼は、半径が無限大になる極限円というものを考えて、平行角の公式

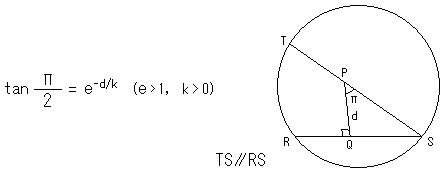
を導き出しました。
極限円の円周は、円でもあり直線でもあるという二重人格のようなモノです。

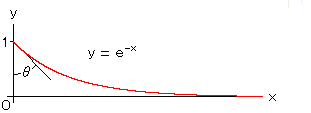
       ちょっと注意がいります。左図は式(*)をそのままｸﾞラフにしたもので すが、赤い曲線はただの指数関数の曲線です。双曲的直線（双曲直線） ではありません。yは平行線間の距離ではく、角θは45°に定まってい て平行角ではありません。式(*)はあくまで考え方の出発点です。

       出発点だけわかっても、平行線は交わるとか交わらないとかをいう ことはできません。しかし、ロバチェフスキーがやったように公準5を否定 することだけから平行角などを導きだすのは、とても難しいといわれています。「19世紀の数学」 という本に寺坂英孝（ひでたか）がロバチェフスキーなどの論文を解説的に訳出していますが、そ れを見ると、平行角を導きだするのに30頁もついやしています。私たちはその難をさけて、モデ ルを活用しましょう。そして、ロバチェフスキーと同じ結果が得られればよいとします。
（同名の本が他にもあり、要注意）

       ［おことわり］
この本は双曲幾何の解説書ではありません。面白い曲線や神秘な曲面を追うのが目的ですが、 ただご覧にいれるだけでなく、すこし本質的なものをみなさんと一緒に覗いてみようとしているので す。
ですから、式の出所もなるべく省きます。ロバチェフスキーと同じ結果が得られているかどうかとい ったことも、同じ結果となったものをお見せするにとどめ、本質を探ることに努めていきます。

１３．平面の形

       平面自体の形なんて、ふつうはありません。平たいだけ です。しかし、双曲界を私たちが見ると写真の紙細工のよう に、それがあるのです。この紙細工には外周がありますが、 それは工作上の制約で、本来の双曲平面はどこまでも広が っています。
       もちろん、双曲界人にとって双曲平面は平坦なものです から、私たちがこの写真を見るときは、実際は波打ったりしな いで平坦なんだと想って見るようにしなければなりません。

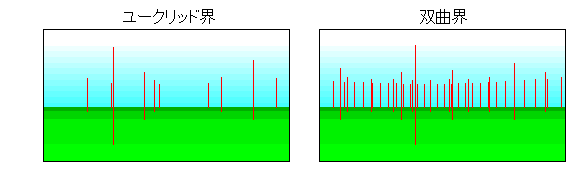
       右の絵は2つの世界 にほぼ等間隔に赤いポ― ルを林立したものです。同 じカメラでそれを撮れば、こ んな風景写真になります。 これはポアンカレ円板での 計算で描いたものですが、 実際にもこうであるに違い ありません。双曲界では遠 くの景色ほど広角範囲が 視野に入ってくるからです。そうです、ユークリッド界から見れば、双曲界の光の進路は曲がって いるのです。それが双曲界の人びとにとっては、やはり光は真っ直ぐに進んでいるのです。双曲界 のほうが賑やかで豊かな感じがしますね。

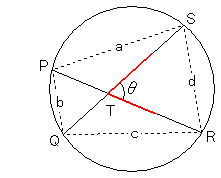
       クライン円板上では右図のように双曲直線はふつうの直線と同様に真っ直ぐな線で すが、双曲角は目に見えているものとは違って、

                             

という関係になっています。これも複比から算出されています。交点が円板の中心のとき は、a = c, b = d となり、ふつうの角と一致します。

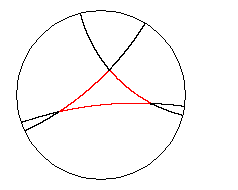
       一方、ポアンカレ円板上では、左図のように双曲角はふつうの角と同じですが、双曲 直線はそうではなくて、無限遠円周に直交する円弧になります。むろん、円板の中心を通 るものは真っ直ぐな直径になります。

       ここで注意しておきたいのは、話はすべてモデル円板上でのことだということで す。私たちが机上で引いた直線がモデル円板上へ変換されると円弧になったりするの ではありません。私たちは、ユークリッド界の無限遠を引き寄せるという発想から出発し ました。ところが、双曲幾何はそうではなかったのです。そうだ、その通りだ。それなら、 ユークリッド界と双曲界を橋渡しするものはないのでしょうか？
残念ながら、ないのです。無限遠や平行線公理にかかわることは、ユークリッド界からまったく隔 絶しているのです。
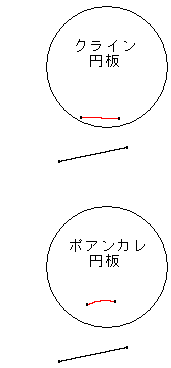
無限遠にも平行線公理にも関係しない孤立した1本だけの線分なら、描けます。右図の赤い線 分は、ユークリッド平面の原点とモデル円板の中心を一致させておいて、黒い線分をモデル側 へ移したものです。しかし、こんなのは何の役にも立ちません。
隔絶しているとはいうものの、後ほど紙細工で工夫してみます。

　

１４．コンパスで円は描けるか

       紙に円を描くのは、コンパスさえあれば簡単ですね。ではなぜ、コンパスをつかうと巧くいくの でしょうか？ 円を描くには、中心が固定されていて、半径が一定に保たれていなければなりませ ん。
ふつう、円というときは平面上のものを指します。紙にコンパスで描いた円は、そのままで円筒に ぴったり貼り付けることができます。ところが、先に円筒に紙を張って、それにコンパスで描いた円 を平面にひろげると、もはや円ではありません。円錐でも同様です。これは説明するまでもなく、コ ンパスでとった半径が曲面に沿ったものではないからですね。

       曲面上で定点から一定の距離にある点の軌跡を曲面円とよぶことにします。曲面円では
  円周＝円周率x直径  といった関係が成り立つのは、伸び縮みしない紙をぺったり張れる面に限 られます。

       球面では*********

       鞍面では*********

       双曲モデル円板では*********

       擬球面では*********

       トーラス面では*********

       円の別の見方
自動車をハンドルを一定の傾きにして走らせると、中心や半径を知らなくてもタイヤの跡が円になります。これにならって点を曲面上で動かすと、やはり円になるでしょうか。

　

１５．曲線の話

       曲線といっても、もつれた紐のようなものは困ります。
平面上のすなおなものとして、まず８の字曲線（レム二スケート）から*************
       レム二スケートの描き方はいろいろありますが、動点が中心を真っ直ぐに通るものと、中心で折り返すものとがあります。パラメ−タをすこし変えると、ハート形や菊形や旭日形にもなります。*********反転すると*********

       クロソイド*********渦の向きを逆にして*********

       卵形、翼形*********（ジューコフスキー、擬球を切る）*********

       双曲平面上の測地線*********


       ［曲面］

       空間曲線（曲面上の曲線）*********

       メビウスの帯上の球、三角形、ベクトル矢線*********

       クロスキャップ*********

       ４次元の影*********

       距離の絶対単位*********

       ＜＜以上を有機的につないだものにしたい＞＞