Ch.18 Lambert's Quadrangle (Analytic Curve) 
The picture [Fig 18-1] right looks like a rocket flying through space, doesn't it?
The edge line of the rocket is hyperbola. The size of this rocket is the same as that of the universe. And it can only struggle. No. It must be flying. Because the infinite universe is never be filled with infinity.
and also .
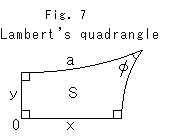
See figure (1) left. Give point P and two segments x,y that right angle to each other at P. And set Lambert's quadrangle. Then move x or y with keeping area S constant, just like an ordinary rectangular hyperbola. Point p is the a point of intersection of asymptote and you get hyperbola like the rocket. (There is no way to express this hyperbola by a single formula like parabola below.)
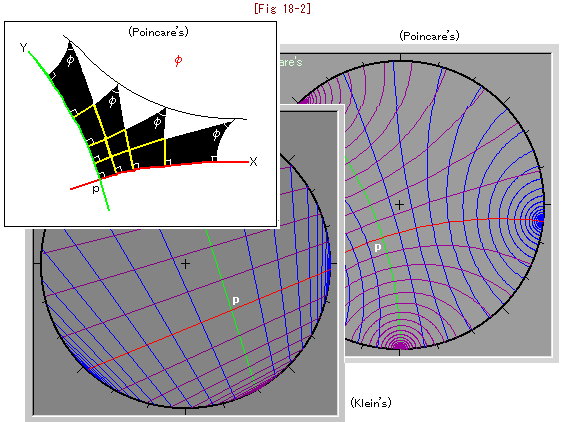
Look at [Fig 18-2] above. Green line is perpendicular to red line. Supposing these lines are ordinary orthogonal axes, I set lines perpendicular to and at regular intervals on each axis. As you see, they are so distorted.
Now a parabola.
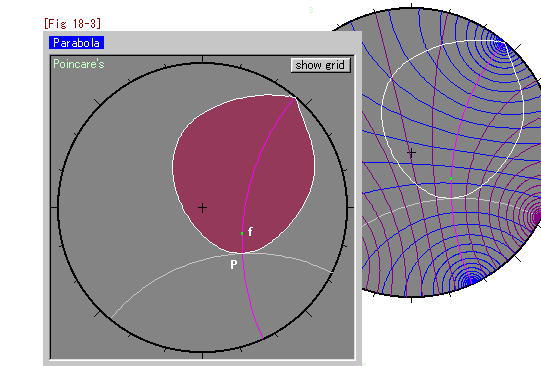
It looks like a colored leave in [Fig 18-3]. Point p is vertex, and green point f is focus.
This figure is plotted;
Let point p be the origin and take a distance Y along pink Y-axis from point p, then
there take distance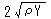 
to the right and left where plot.
Popular formula is written below, but all are hyperbolic value.
Seeing [Fig 18-3], the curve looks closed at a point of infinity. How is it truly?
You may have seen a picture like figure (2). It partially represents the actual object in case you imagine. We do not call it a model. But the following is true on what is called projective plane (cf. Ch.27).
They say all quadratic curves are closed when homogeneous coordinates or projective plane is applied. An ellipse does not touch the line at infinity. A prabola is closed and touches the line at infinity. Since a horocircle touches the line at infinity, a horocircle belongs to a prabola.
A hyperbola is also closed, and crosses over the line at infinity. The other side of the line is not farther than infinity. For instance, on a disc model, it is the inside area of opposite side. In other words, to go across the line at infinity is to jump to opposite side of the disc. The circumference of the disc is the line at infinity. And we identify a point on the circumference with a opposite point in respect with the origin. That is so called identification in mathematics.
Well, it looks like sophistry contest, doesn't it? How can we get to the end?
No one has been to infinity.
We have no information to judge what infinity is.
There is a few circumstantial evidence, but not strong enough.
Consequently, we should define infinity rather than making a question. The definition must be reasonable, of course. That is what we are looking for.
Previous: Ch. 17 Horocircle 1 (Hemisphere)
Next: Ch. 19 Area Density and Sector
Table of Contents
Index