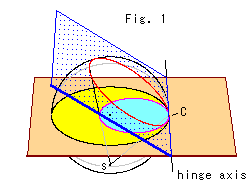
We got a circle when the hemisphere was sliced with the Hinge Axis was located outside the hemisphere, and we got an equidistant line when the Hinge Axis was inserted into the hemisphere. What will happen if we put the Hinge Axis just in contact with the edge of the hemisphere?
Look at Fig. 1 right. The yellow disk is Poincare's disk model. The red upper ring is the cut end of the hemisphere. It is projected to the south pole S, and makes the sky blue circle on the disk model. This sky blue circle is so strange that it has a special name horocycle.
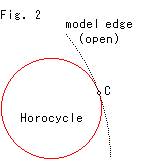
The center of the horocycle is located at point C on the model edge that is a point at infinity as shown in Fig. 2. The circumference of the horocycle goes through point C, too. The center C is on the circumference!
The disk model is an open domain so that the horocycle is not a closed circle (loop).
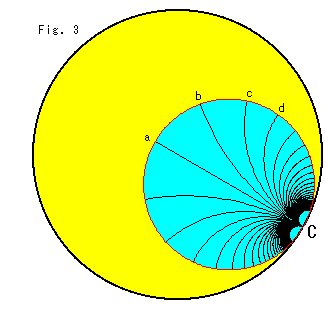
Fig. 3 shows a horocycle on Poincare's disk model. The white lines aC, bC, cC, which are straight and radiate from the center C, are perpendicular to the circumference. All of their length is infinity regardless of point C itself. Then, we may write
= 
.
Points b, c, are drawn at regular intervals from point a for easy observation. But all the central angles with respect to center C are zero whatever the intervals are.
= 0 .
This is because all radii are parallel with common point C. But, judging from the figure, we feel that the totaled central angle is 180
. Wait. Do not treat the horocycle as if an ordinary circle. In this case the concept of ordinary central angle is not in use.
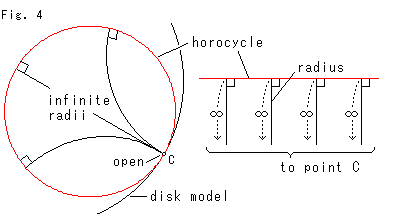
Look at Fig. 4.
All the radiii of horocycle is infinitely long and forwarding to point C. The horocycle is the same as Lobachevsky's limit circle, isn't it? Therefore the horocycle is also a straight line.
Hyperbolic trigonometry is not applicable to a triangle with vertex at infinity.
Look at Fig. 5.
It shows equidistant lines on Poincare's disk. The green curves (circular arcs) are the base lines and the red lines are equidistant lines with respect to the green. Now move a base line to point C at infinity as directed by arrows. Then finally the green base line becomes point C and its red equidistant line forms an osculating circle to the disk edge. That is to say, the equidistant line becomes a horocycle.
At any rate, a horocycle is a circle and a straight line at atime, say "the horocycle is a a person with a dual personality", you know.
Since the horocycle touches on line at infinity (disk edge), it can also be called a parabola from the view point of projective geometry that we will see later.
We saw in Ch. 13 that the movement along equidistant lines makes parallel translation. Then, how about the movement along the horocycles?
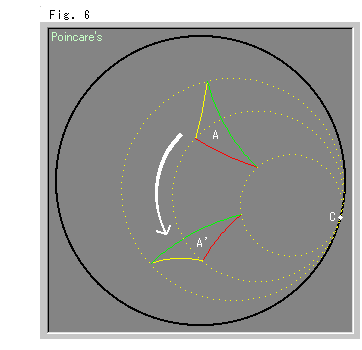
Look at Fig. 6 right.
We move triangle A along horocycles by reflection (twice). Triangles A and A' are congruent, and the movement is a hyperbolic parallel translation. The distance from point C to each vertex is infinity . But if we regard it invariant constsnt, this movement is also a hyperbolic rotation.
However, we don't know if the triangle continuously pass point C? Does the triangle becomes a point at point C, or does it disappear a moment? It is qiute strange that translation and revolution are the same, isn't it?
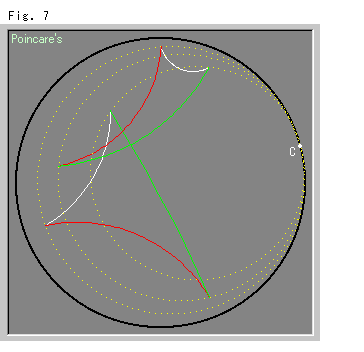
Look at Fig. 7 left.
It is similar to Fig. 6. We choose a large triangle. The triangle looks to change in size and shape, but not actually. It is congruent all the way of movement. The horocycles here are concentric circles.
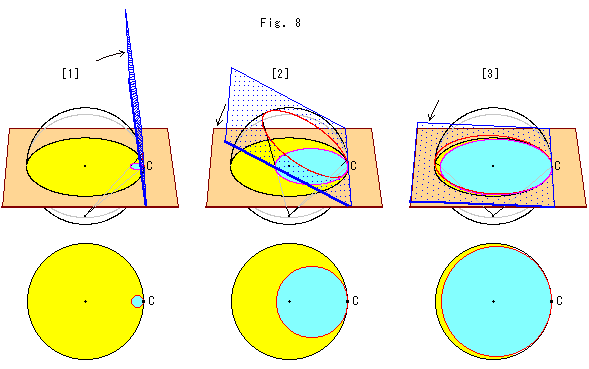
Look at Fig. 8 above.
We turn the Slicer around the Hinge Axis which is fixed to the edge of the hemisphere.
[1] shows when the Slicer is turned up. If we raise it up vertically, the horocycle becomes point C.
[2] shows when the Slicer is leaned. The horocycle gets bigger.
[3] shows when the Slicer is leaned more and close to being horizontal. If we turn it down horizontally, the horocycle becomes the same size as the yellow model disk. But the center of the horocycle stays always at point C.
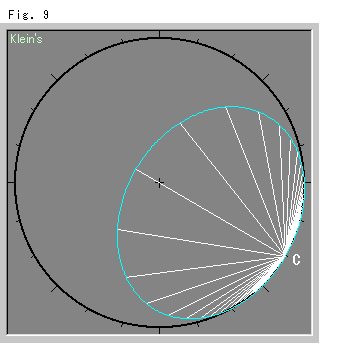
Look at Fig. 9 left.
It is a horocycle drawn in Klein's disk model that shows a hyperbolic straight line as a visually straight line.
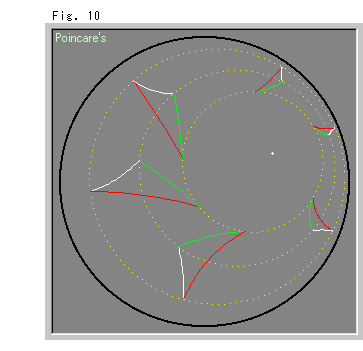
Fig. 10 shows the rotational motion of a triangle on concentric circles with the center (white spot) located inside Poincare's disk. Compare it with Fig. 6 or Fig. 7 of horocycles.