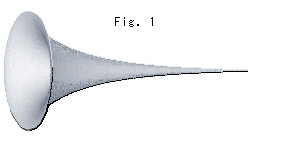
Here we see what is called Beltrami's Pseudo-sphere. It shows the real Hyperbolic Non-Euclidean World (plane) as it is.
A Pseudosphere is like a music horn with an infinitely long tail as shown Fig. 1. It is a part of hyperbolic plane if we regard the surface as flat and geodesic as straight line.
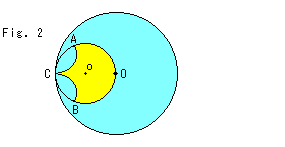
Look at Fig. 2.
Let's make a Pseudosphere from Poincare's disk model. The large circle O is the disk model. The small circle o is a circle with a diameter of OC. Point O is the origin (center) of the disk model, and point C is on the circumference (infinity) of the disk model. That is, circle o is a horocycle. Point C can be located anywhere on the circumference of circle O. Circular arcs AC and BC in circle o are perpendicular to the circumference of circle o. The hyperbokic length of circular arc AOB is 2
. Now, we cut out the yellow sector from the disk model.
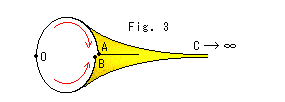
Look at Fig. 3.
Suppose the cutout is a soft material, and extend it so that its length becomes a true hyperbolic length when measured ordinarily. And glue lines AC and BC. Then the cutout becomes like a music horn as shown. We may imagine that the cutout is automatically wrapped up like a spring and infinitely thrusts its tail when we take it out from hyperbolic plane (the disk plane) to our Euclidean space.
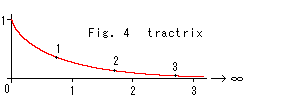
Look at Fig. 4.
A Pseudosphere is a surface of revolution. The red curve is a so-called tractrix that is the generator of surface of revolution of Pseudosphere. The numerals on the tractrix are distance from the skirt.
On the surface of a Pseudosphere, let's say that
the geodesic (shortest path) is a straight line,
and the curved surface is regarded as a plane.
Then we get the Hyperbolic Non-Euclidean World perfectly reproduced in our Euclidean World. We do not need any special ruler or protractor. It is just as we observe it. How marvelous it is!
Look at Fig. 5 below.
Rays from point C are hyperbolic straight lines. Curves like concentric circles are equidistant lines with a regular interval of 0.5. They are not hyperbolic straight lines. The hyperbolic length of arc AmOm'B is 2. Point m is the middle point of arc AO and point m' is that of arc OB. The dark-colored area on the sector corresponds to the opposite side of the Pseudosphere and it has been included to help you grasp what is being discussed. The triangle has been added so that you can see the correspondence to the Pseudosphere.
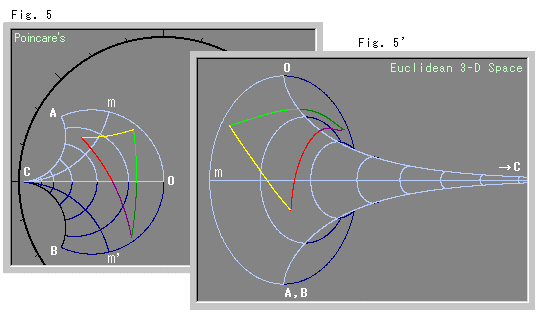
Fig. 5' is a Pseudosphere made from Fig. 5. The largest radius of the Pseudosphere is 1. (The drawing scale of Fig. 5' is smaller than that of Fig. 5.) The rings are at regular intervals of 0.5 ordinarily measured on the surface of the Pseudosphere. They correspond to hyperbolic concentric circles in Fig. 5. The triangle on the Pseudosphere looks larger, but actually it does not change from Fig. 5 in both angle and length. In Fig. 5', they are drawn showing the real hyperbolic distance.
We used Poincare's disk but we get the same result as Fig. 5' with Klein's disk.
Unfortunately, however, we cannot reproduce the whole Hyperbolic Non-Euclidean World. We are sorry in particular that we cannot see what occurs around the origin O. Hilbert had proved the impossibility of this.
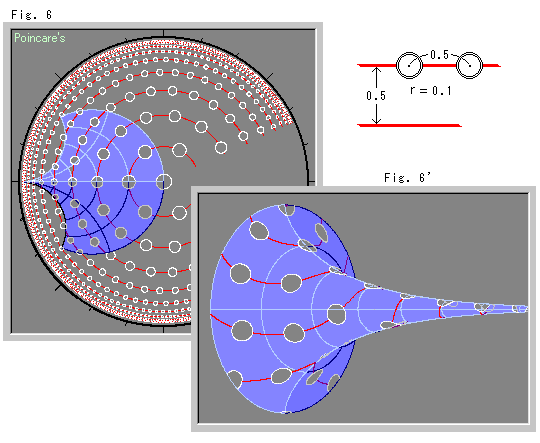
Look at Fig. 6 below.
Let's confirm if the Pseudosphere shows the Hyperbolic Non-Euclidean World. We draw red hyperbolic concentric circles on the disk model, and place small white hyperbolic circles on each red circle at regular intervals of 0.5. The interval of radii of red circles is 0.5. The radius of every white circle is 0.1. The white circles on the right area have been omitted because we cannot make it around with regular intervals. Now we cutout the disk and make a Pseudosphere.
Fig. 6' shows that the red concentric circles are certainly at regular intervals and that all the white circles are surely the same in size and placed at normal, regular intervals. Every white circle is formed in a small saddle shape.
The shape of a cut-out can be non-symmetrical like Fig. 7. Also we can cut the disk widely as shown in Fig. 8. And we can illuminate where we want to see. Let us call it a multi-layer Pseudosphere.
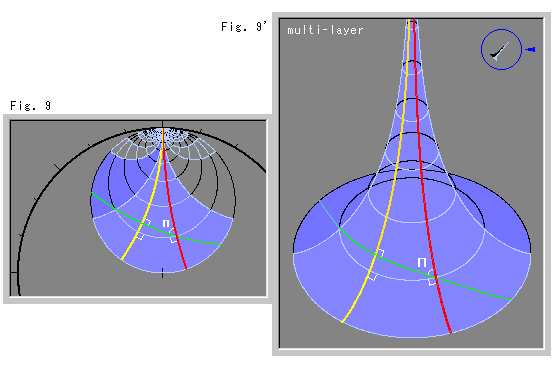
Look at Fig. 9.
Here, we have cut out the horocycle entirely and gotten a multi-layer Pseudosphere, but what we observe is only the colored single layer. The light-colored part is our side of the Pseudosphere on the screen. Two straight lines colored in red and yellow are parallel lines. We can certainly expect that the red and yellow lines meet at infinity, and we can accurately measure the parallel angle 
on the Pseudosphere embedded in Euclidean space. The ring lines (concentric circles in the disk) go perpendicularly across both the red and yellow lines, but they are not straight lines.
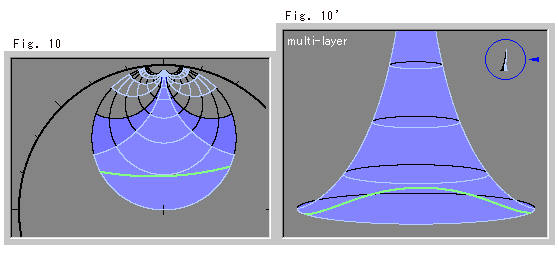
Fig. 10 and Fig. 10' above show a straight line drawn nearly horizontally.
Fig. 11 and Fig. 11' below show a straight line drawn at a slant. In Fig. 11', the line goes up, winds itself around the tail, and comes down.
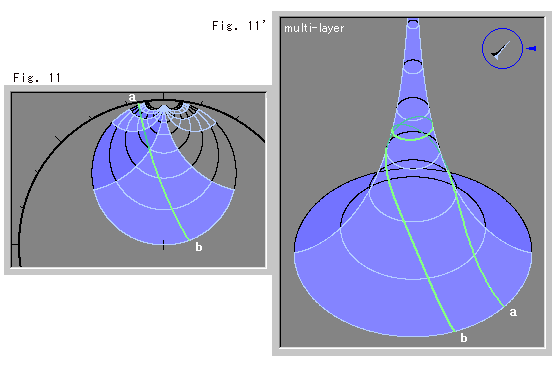
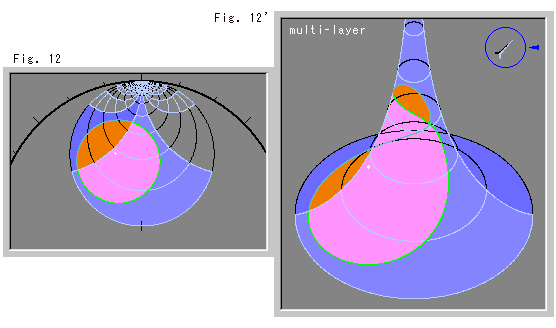
Fig. 12 is a circle. The white point is its center.
Fig. 12' is the reproduction of circle on a Pseudosphere. It is clearly a saddle. Just regard the saddle as a plane surface. Then you can see that hyperbolic geometry stands up on the "plane" using ordinary measurement.
The saddle will have a double part (as shown in Fig. 13) when we change the size or location of the circle slightly. The doubling does not occupy the same face, but rather the layered face of multi-layer Pseudosphere.
Fig. 14 results when we chang the circle some more. The saddle winds itself around the tail. Coloring is omitted deliberately.
Now we understand that everywhere in a hyperbolic plane on a Pseudosphere forms a saddle. Then how about the area around the origin O of the model disk? We guess that it is also like a saddle if limited to an extremely narrow width.
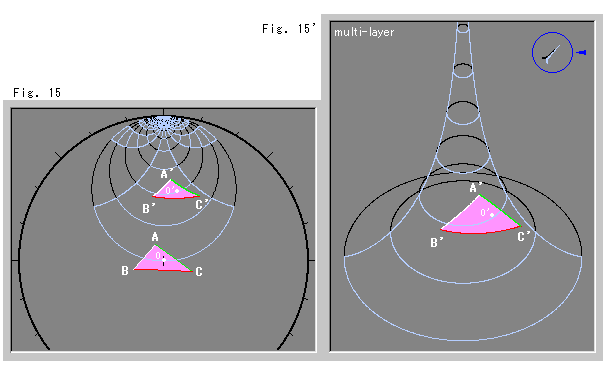
We cannot reproduce a model disk that includes the origin O inside it on a Pseudosphere. However, we can move triangle ABC onto a horocycle as triangle A'B'C' keeping congruence. And we can reproduce a new triangle A'B'C' on the Pseudosphere as shown in Fig. 15'. The white point O' is a copy of origin point O that was inside triangle ABC.
If we interpret this copied point O' as the origin with respect to triangle A'B'C', the result is that we get triangle ABC with the origin O inside. Though we could not reproduce the real origin O on a Pseudosphere, the relationship between the new triangle A'B'C' and the new origin O' are identical to that of the original triangle ABC and the original origin O. Thus, we can see on a Pseudosphere any figure that includes the origin point if it can be moved completely onto a horocycle.
A surface that is the result of dragging out a multi-layer Pseudosphere is called a "Dini's surface". The picture in Fig. 16 was drawn by Tore Nordstrand. We copied it from Gallery of Curved Surfaces on the Internet. How beautiful it is! It looks like a petal, doesn't it?
Another web-page about Pseudospheres is la pseudosphere. It is in French. Even if we do not understand French, we can enjoy the pictures.
A Pseudosphere can also be made from a model called an Upper-half Plane. We will see it in Ch. 21. Historically, Beltrami's Pseudosphere was the first model introduced, before disk models (Poincare's and Klein's) and the Upper-half Plane.