The upper half-plane is one of models for the Hyperbolic Non-Euclidean World (a plane). It does not show us a panoramic view of a hyperbolic plane, but it is quite useful for making simple calculations, to see the relationship with horocycles or Pseudo-spheres, and especially to think about infinity. The upper half-plane is often denoted by 
.
Here we will see how the upper half-plane is compressed or expanded. And we will see what straight lines and distances in the upper half-plane look like.
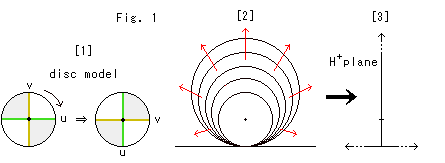
Look at Fig. 1.
We are familiar with Poincare's disk model. So let's make the upper half-plane from the disk model.
[1]: First, we turn the disk clockwise 90
as shown.
[2]: And we fix the center and bottom, and expand the disk infinitely.
[3]: Then the lower part of circumference becomes a horizontal straight line, and all the other part have gone to infinity. Thus we get the upper half-plane . (There are some other ways of making the upper half-plane from Poincare disk. We will see them later.)
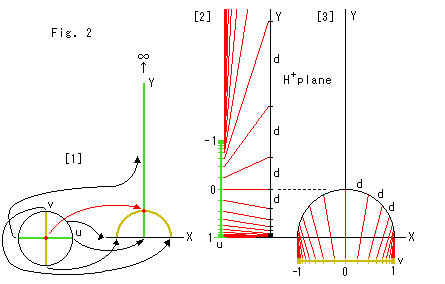
Look at Fig. 2.
It shows correlation between Poincare's disk model and the upper half-plane. Let us denote the horizontal and vertical axes of the disk model by u and v respectively, and those of the upper half-plane by X and Y respectively.
[1]: The u-axis transfers to Y-axis (y > 0) with setting the positive end point (right end, u = 1) of u-axis on the X-axis. The negative end point (left end, u = -1) of u-axis goes up infinitely. The v-axis transfers not to the X-axis but, the semicircle on the X-axis. In the upper half-plane a hyperbolic straight line becomes a semicircle on the X-axis or a vertical line standing on the X-axis. So the origin (center) of disk transfers as shown with the red arrow. What transfers to the X-axis is the circumference (line at infinity) of disk.
[2]: We intentionally set the u-axis in vertical and graduate in 0.5 hyperbolic length. The corresponding graduation on the Y-axis is visually a logarithmic scale. The red lines show their links. (There is no zero in logarithmic scale.) The length of every d is, of course, 0.5 in hyperbolic length.
[3]: The v-axis is intentionally set in horizontal. It is also graduated in 0.5 hyperbolic length. The corresponding curve of v-axis is not on the X-axis, but it forms a semicircle on the X-axis. The length of all d on the semicircle is 0.5 in hyperbolic length, too. The scale on the right and left part of the semicircle looks logarithmic, but in reality it is not.
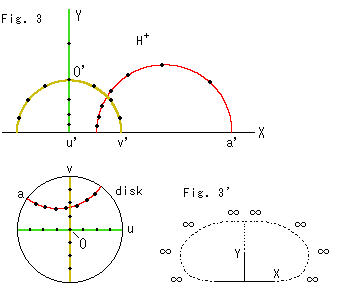
Look at Fig. 3.
Lines in the same color correspond each other. The red lines are hyperbolic straight lines that are not on any axis. The black spots are corresponding points that are plotted on Poincare disk at Euclidean regular intervals. In the upper half-plane corresponding points on a semicircle are not symmetrical unless the semicircle itself is symmetry with respect to Y-axis. End points a, u, v transfer to a', u', v' respectively.
Look at Fig. 3'.
We said that the negative end point (left end, u = -1) of u-axis goes up infinitely. But it is not so certain. The end point is also on the circumference, so that it must be transfered to X-axis. Well, it is inconsistent. However, this problem has already been settled cleverly.
The upper half-plane is open in every direction as well as the disk model. X-axis is not an ordinary hyperbolic straight line. You may imagine like Fig. 3'. But the following idea seems better.
Poincare's disk is an open disk and we can draw it with its entire boundary (circumference). And it is the upper half-plane that is deformed from the disk to another open plane. The boudary of upper half-plane is not what come unsewed but drawn partially.
In addition, it may be nonsense to search the destination of left end point of u-axis because no one can get to the left end point from inside. In our field of vision X-axis is the bottom of a circle with infinite radius, and Y-axis is the foot of a semicircle with infinite radius.
The X-axis is a line at infinity, and so we can not define distances on it. Therefore there is no graduation on X-axis. It is only Y-axis that we can graduate. But in the upper half-plane (y > 0) we are able to say distances in the X-dirextion, of course.
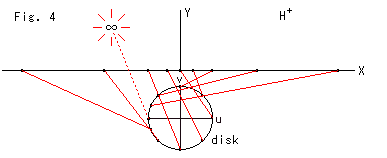
Look at Fig. 4.
It shows how points on the circumference of Poincare disk move onto X-axis of the upper half-plane. We placed the disk just under the upper half-plane for easy observation. The red lines link corresponding points. They are twisted because the disk is not turned by 90. There is one-to-one correspondence between the circumference of disk and the X-axis though we have no graduation on the X-axis with the exception of the left end point of disk. We comically illustrated the exceptional correspondence (one to ?) like a firework.
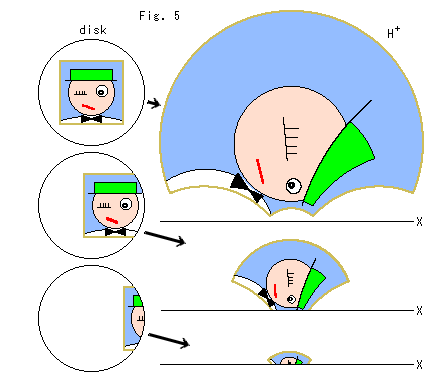
Look at Fig. 5.
It's just for fun but qite helpful to understand the relationship between Poincare's disk and the upper half-plane. Compare this picture with above Fig. 1 to 4.
Let us see the upper half-plane itself.
As for an angle, it is the same sa that of Euclidean as well as Poincare's disk. So we see about length. (We will see about mertic later.)
A Geodesic line, excluding the vertical direction, is a semicircle visually. It is not clear at this moment, though we can guess somewhat from Fig. 2. Neither, we have not yet gotton an answer for the question why a straight line in Poincare's disk model is a circular arc that perpendicular to the disk edge. We will see them later on. Here let us see how hyperbolic straight lines stay in the upper half-plane.
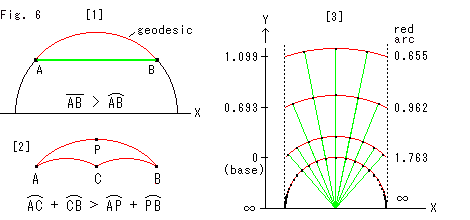
Look at Fig. 6.
The red visual arcs are hyperbolic straight lines. There is no hyperbolic straight line parallel to the X-axis.
[1]: The green segment is not a hyperbolic straight line though it is visually parallel to the X-axis. In hyperbolic distance, the red circular arc is shorter than the Green segment. It is truly "More haste, less speed."
[2]: When we travel from A to B, route A-C-B is longer than route A-P-B. Addition and subtraction in hyperbolic distance stands up with respect to a single hyperbolic straight line (a vertical straight line or a semicircle on the X-axis). These things do not depend on where the Y-axis is.
[3]: The left scale is hyperbolic distance from X-axis at Euclidean regular intervals. The base point is at Euclidean distance y = 1 from X-axis. You may use negative scale under the base point. The numerals at right are hyperbolic length of the red arcs. Those length (distances), in relation to the X-axis, the farther we get from it, the shorter the hyperbolic distance becomes, though visual distances are the same as the upper and lower. The black spots are at hyperbolic regular intervals measured from a middle point of an arc. The bottom arc is a semicircle on the X-axis and, naturally, its length is infinity. We tried drawing lines that pass the black spots, and got green rays from X-axis as shown. We will see them next.
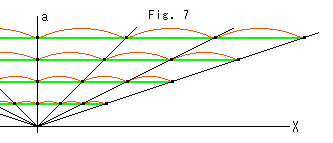
Look at Fig. 7.
The straight line a is perpendicular to the X-axis. The length of all the red "straight" lines is the same, and the length of all the green "curved" lines is also the same. Every red line is shorter than any green line, of course. The slant black straight lines are the same as those of
the geen lines at {3} in Fig. 6. They ray from a point on X-axis. That means we can not define distance on the X-axis.
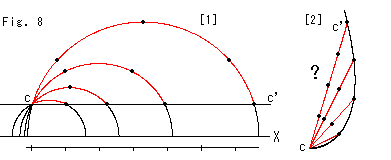
Look at Fig. 8.
[1]: Visual semicircles are hyperbolic straight lines that pass a common point c. The right end points of the red circular arc are all in the X-direction. This is indicated by the black line cc'. The black points on the red circular arcs are at regular intervals of the smallest arc. That is to say, starting at point c, we can quickly get to our destination on the line cc' if we go along the red hyperbolic straight line. Compare it with the scale drawn below the X-axis.
Red routes start from point c in the different direction depending on each length. It is due to the fact that the black line cc' is actually not a straight line but a curved one.
[2]: It might possibly look like this for residents of the Non-Euclidean World.
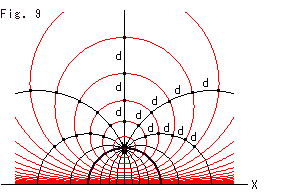
Look at Fig. 9.
It shows hyperbolic concentric circles and its radius rays. The interval of each circle is constant d. The angle between each adjacent radii is 
/8. The thick black semicircle is the series of diameter of the concentric circles.
Hereafter we omit adjective "hyperbolic" when an object (straight line, distance, etc.) is obviously in the hyperbolic space unless we want to stress it.
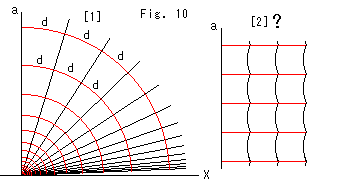
Look at Fig. 10.
[1]: The red lines are straight lines and drawn at regular intevals. The black ray lines that stand on the X-axis are equidistant lines with respect to the perpendicular line a. The length of every red straight line caught between these lines is d. The black equidistant lines are not straight lines, except line a. That is to say, the distance between two red lines measured along a slant black line is not constant. Generally in hyperbolic geometry, when we say "distance", it means distance measured along a hyperbolic straight line (geodesic). It is similar to Euclidean geometry.
[2]: It is an imaginary picture that residents of the Non-Euclidean World might see.
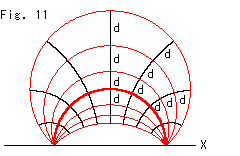
Look at Fig. 11.
The red lines that look like circles in the wane are equidistant lines with respect to the red thick straight line (semicircle). The black lines intersect orthogonally the red equidistant lines. The length of every black straight line caught between these red lines is d. The thin red equidistant lines visually look circular arcs but neither hyperbolic circles nor straight lines.
A hyperbolic circle is drawn as a circle in the upper half-plane as well as Poincare disk. However, it never cuts the boundary (X-axis).
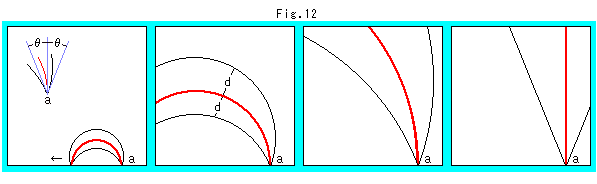
Look at Fig. 12 below.
The bottom of each picture edge is X-axis. The black lines are equidistant lines with respect to the red straight line (semicircle). The interval d of every equidistant line from the red line is always the same. Observe from left to right. We fix the right end of the red straight line and move the left end of it to far left. The angle 
in the very left picture is the angle formed with three lines at the point a. This angle does not change wherever the left point is located on X-axis. Because the figure changes only in Euclidean similarity. The very right picture shows a case that the left end of the red straight line has gone to infinity. And equidistant lines are not circular arc but straight lines. We guess that all of straight equidistant lines and the red straight line gather at infinity. But we are not sure yet.
Imagine a situation when the angle gets bigger upto 90.
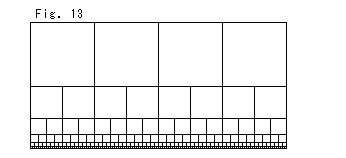
Look at Fig. 13.
It is a digitized Upper half-plane . Squares get bigger as they go up doubling every step. But they are actually constant in the upper half-plane .
Let us uniform all squares in Fig. 13 by force. If we do so, we get a picture like Fig. 14. It is somewhat close to the actual hyperbolic plane.
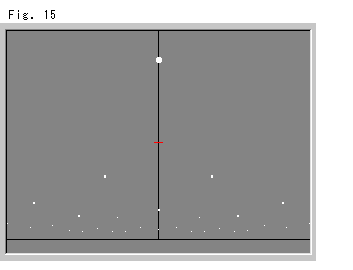
Look at Fig. 15.
It shows equally spaced spots. Their sizes and intervals look bigger when they get further from the X-axis, but in the X-direction they are constant. The red mark - on the Y-axis is a base point for the drawing.
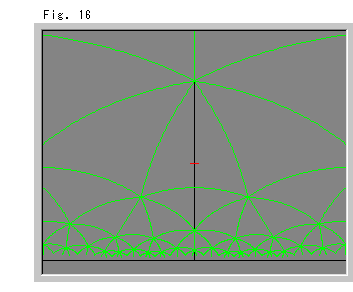
Look at Fig. 16 right.
It shows straight lines that connect the centers of adjacent spots in Fig. 15. Every triangle is a congruent regular triangle with a 2/7 interior angle. In short, it is a tiling.
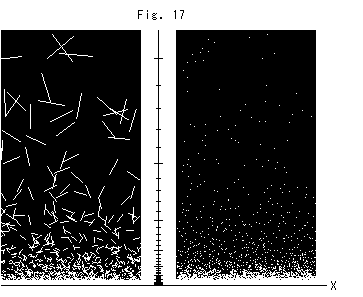
Look at Fig. 17.
It shows hyperbolic seguments and dots spread in the upper half-plane. The length of all the segments in the left picture is equal. Every segment is a cicular arc (part of semicircle) which center is on X-axis though it looks straight. It is sparse in the upper region and more concentrated in the lower region. It is perfectly solid on the X-axis. The right is of hyparbolic spray. Thus visual density in the vertical direction changes. But in the X-direction (at constant Y) does not change.
We will occasionally use the upper half-plane.