Euclidean geometry avoids infinity. Metric and curvature, which we have looked at in previous chapters, also avoid infinity. This is not sufficient. The study of inversion will supplement what we have learned so far about metric and curvature. Here we will concentrate on inversion, and think about infinity.
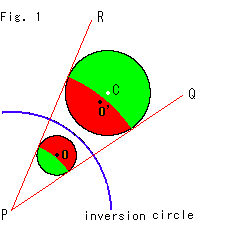
Look at Fig. 1.
Small circle O is inverted to big circle O' with respect to the blue inversion circle. Colored portions correspond to each other. Point O is the center of circle O, but point O' (the inversion of point O) has slipped toward the center P of the inversion circle.
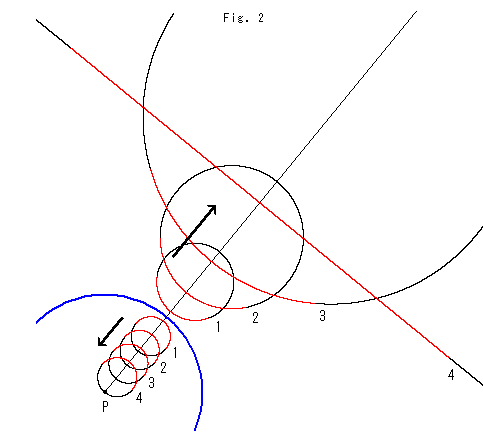
Look at Fig. 2.
The blue circle is an inversion circle. For now, let's call circles inside the inversion circle "In-circles" and circles outside the inversion circle "Out-circles". In-circles and Out-circles are invertible with each other. All the In-circles are the same size and half their circumference is colored sky blue. The colored portion of the Out-circles correspond to that of the In-circles.
When we move an In-circle toward the center P of the inversion circle, the Out-circle gets bigger and goes farther away. Also, the red tangent lines open wider and wider. When the In-circle arrives at point P, the tangent lines become the straight line R'PQ', and the point on the Out-circle that corresponds to point P goes to infinity.
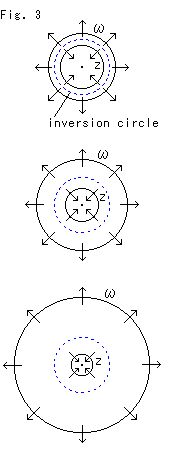
Look at Fig. 3.
The blue dotted circle is an inversion circle with radius 1, and its center is located at the origin. The center of circle Z (with radius r) is also located at the origin. Circle 
is an inversion of circle Z. Since Z is a circle, becomes a circle. When we shrink circle Z, circle rapidly gets bigger. The relation between radius r of circle Z and radius R of circle is
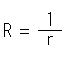
When we push r infinitely close to zero,
And radius R of circle becomes infinity 
. So we can determine that the relationship between Z and
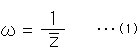
is
= for Z = 0.
That is to say, we define
Usually fractional numbers with zero denominator cannot be defined, but here we will presume to do so. (If this is a problem for you, try thinking of it in terms of limitation.) Here we do not care whether infinity is positive or negative.
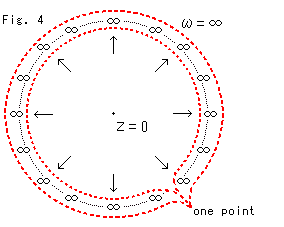
Fig. 4 is an illustration showing what happens when Z = 0. flies off in all directions infinitely, and the infinite continuously flies at an infinite speed. If so, the one to one correspondence between Z and cannot be maintained. Therefore, mathematicians take the position that all points are regarded as one point. This does not mean that all the points are gathered up at infinity. This appears northern, southern, eastern and western directions, and yet it is a single point. On the contrary, this also means that becomes = 0 when Z = , and the one to one correspondence is maintained. Then, the single point is named at infinity and denoted by .
Frankly speaking, this naming is not proper because we take it to mean that it is a point that stays at infinity. It is not always wrong, but the point is only for consistency in one to one correspondence. Any point will do unless it is used to represent some other point. It can also be a fictitious point.
There is another unsuitable thing. A point at infinity is denoted by , which is a symbol that is used for infinity. The point at infinity is a point and infinite in size. sometimes means infinite distance. We occasionally distinguish plus and minus infinity, and we denote negative infinity by -. In other cases, infinity has no concept of positive and negative. A point at infinity is positive or negative at the same time, and yet neither positive nor negative. We therefore will denote a point at infinity by 
rather than , and we will try to define its meaning.
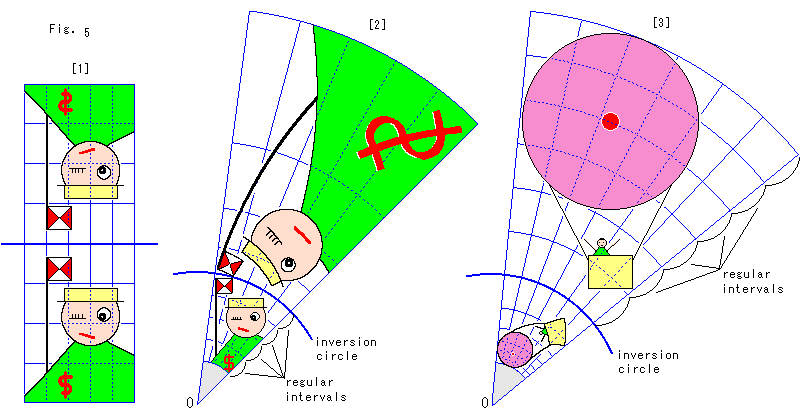
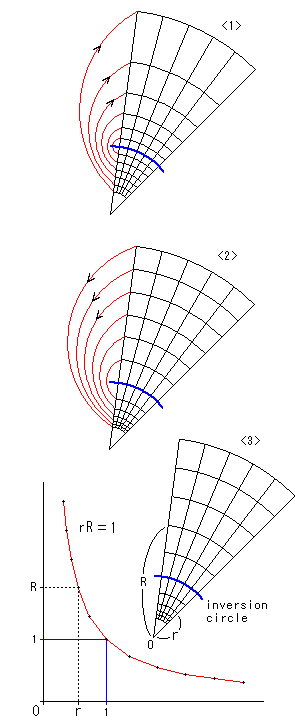
Fig. 5 is drawn just for our fun.
[1]: It is a usual axial symmetry.
[2]: We drew a picture inside of the inversion circle and inverted it to the outside. So we set concentric circles in the inversion circle at regular intervals and we inverted them to the outside as shown figure right <1>. The grid does not corresponds to [1]. Pictures inside and outside are in inverse to each other. So there is no particular reason for the regular intervals.
An inversion is a conformal mapping. See the picture inverted and enlarged. The flagstaff is bended and the dress is widened like a skirt. But the angle between the flagstaff and the edge of clothes is not changed at all. That is to say, angle at every point is unchanged though shape and size changed.
Yes, it is true. Nevertheless it is strange. [1] is what is simply reflected. We can get [2] from [1] by compressing one side and expanding the other side. It is so distorted. Why do not anges change? It is easy for us to accept the fact that angles are unchaged. But, why is it so?
To the contrary, pictures can be regarded as normal if we use a ruler and a protractor that are distorted to meet the distotion of grid at ever point. It is natural and we do not feel strange. One thing is strange and anothe is not. Why? Well, let us push on anyway.
[3]: This time, we drew a picture outside of the inversion circle and inverted it to the inside. So we set concentric circles outside of the inversion circle at regular intervals and we inverted them to the inside as shown figure right <2>. A circle is a circle after inversion unless the original circle passes the the center of inversion circle. But the center of a circle slips by inversion.
See figure right <3>. It is drawn with concentric circles based on points at regular intervals along the red hyperbola rR = 1. No circular grid is at regular intervals. We used the radius of 1 for the inversion circle, but the grid pattern does not depend on the size of the inversion circle.
Fig. 6 shows how curves (including straight lines) change by inversion.
The blue circle is an inversion circle. Curves in the same color are mutually inverted one to the other except the yellow one. Points on the yellow straight line that passes the center O of the inversion circle move by inversion but the straight line itself does not change. Thick parts correspond to each other. The black curves are a square and its inverted. Needless to say, all the points on the circumference of inversion circle does not change by inversion.
Point P is getting to the center O of the inversion circle. And point P' that is the reversal of point P is going far away to the left below, we guess. Similarly point Q is getting to the center O, and point O' is going far away to the right below.
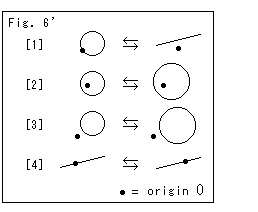
A circle and a straight line change by inversion as illustrated in Fig. 6'.
[1]: A circle that passes the origin O changes into a straight line that does not passes the origin O.
[2] and [3]: A circle that does not pass the origin O changes to a circle that does not passes the origin O.
[4]: A straight line that does not passes the origin O does not change (fixed line).
This is OK in the area we can see with our own eyes. But how about point P' and point Q'? Point P and point P' are continuously related in one to one correspondence unless point P arrives at the origin O. Suppose point P is now staying at the origin O. Then point P' must be leaving (moving) at infinite speed at infinity. And still one to one correspondence is kept. The same situation happens between points Q and Q'. Both point P and point QQ are at the origin, and point P' and point Q' are separately in the different direction. Nevertheless, in Fig. 4 point P' and Point Q' together are at one point that is the point at infinity . Is that really OK?
We understand the mechanism of inversion. But it is not enough to feel concretely. So we pay attention to the fact that a model disk and the upper half-plane 
can be changed to each other by inversion. Let us see it carefully.
It is not necessary a model disk and the upper half-plane . An ordinary circle and a half-plane will do. So we specify which is which if they are to be hyperbolic models.
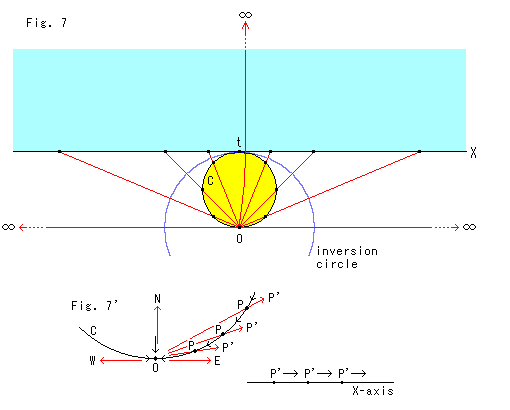
Look at Fig. 7.
The blue big circle is an inversion circle with the center O. There is a yellow inscribed circle C that passes the center O and contacts the inversion circle at the top.
Circle C becomes X-axis of the sky blue half-plane by inversion. The red lines show their correspondence. The inside of circle C spreads over the half-plane that is unlimitedly wide-open. The point that contacts the top t does not move by inversion.
Look at Fig. 7'.
Suppose point P on the circumference of circle C is at point O. Where does it go by inversion? Does it explode, and yet a single point like Fig. 4? Is it realy OK to think so?
Let us think about it with the idea of limit. Point P comes gradually from the right to point O. The inverted P' jumps onto X-axis and moves to right and right. When point P arrives at point O, point P' must be at infinity right E.
On the contraly, if point P comes gradually from the left to point O, point P' must be at infinity left W. If point P inside the circle C comes perpendicularly down to point O, point P' must be at infinity up N.
In a sense, we can say that the inversion at point O is decided by the comming direction of point P. However, every point on the disk C does not move itself. Then, what about point O itself that had stayed from the beginning? It has gone somewhere outside of finite territory. We can not help but guess that point P' turned itself into a point at infinity having no fixed address.
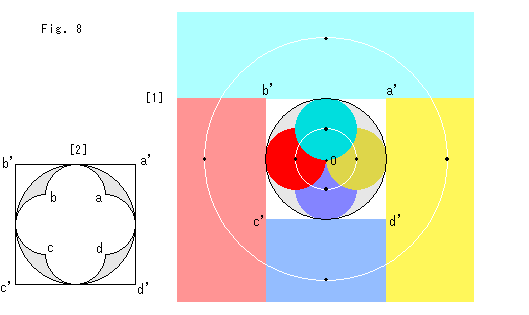
Look at Fig. 8.
We color areas inside and outside of an inversion circle to see which part is inverted to which part.
[1]: Four circles are inscribed in the inversion circle and pass the center O. They are colored dark and inverted to outside of the inversion circle and get bright color. The white area at the corners of square a'b'c'd' corresponds to the gray area. Black spots are the centers of the four circles and their inverted points. White circles are passing those centers and correspond to each other.
[2]: Corresponding parts of square a'b'c'd' and the gray areas. Well, it looks like playing games. But it is surely caused by inversin rule.
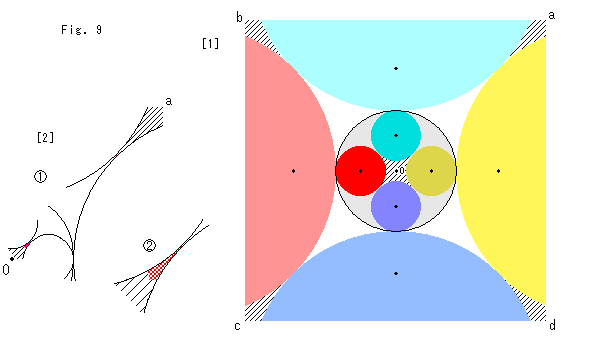
Look at Fig. 9.
Four inscribed circles are set without overlapping. They contact each other as shown.
[1]: None of the four circles passes the center O of the inversion circle, so taht what inverted are circles. But the center of every inverted circle is shifted toward the cnter O. Coloring is the same as Fig. 8.
[2]: The domains with blique lines at the largest corners a, b, c and d correspond to the domains with blique lines in the inversion circle. But actual drawings at a, b, c and d is very little. The red area in 
correspnds to the drawn area at corner a. 
is an enlargement of the red part in .
Look at Fig. 10.
We set the inscribed circle C in the inversion circle. This time, we lay four circles similar to Fig. 4. The gray part in the inversion circle transfers to the mosaic area between line 
and line 
. Line passes the the center O of the inversion circle. Line contacts the inversion circle. Things in circle C transfer to the area between between and line 
, excluding the blue circle. The blue circle transfers to the upper half-plane on and above the line .
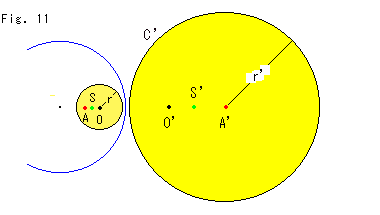
Look at Fig. 11.
How do the center of a circle and the center of invertd circle move? The black center O of circle C becomes the black point O' and the red center A' of circle C' becomes the red point A. Point S and point S' do not change as similar points. That is, OS / r = A'S' / r'.
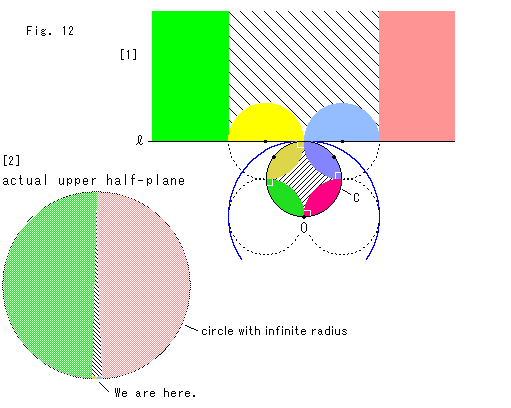
Look at Fig. 12.
We set the inscribed circle C in the inverse circle. The circle C passes the center O of the inverse circle. And we draw four circles that cut the circle C orthogonally.
[1]: It shows the inversion of four domains in the shape of 
.
Suppose the circle C is Poincare disk. Then circular arcs in the disk are hyperbolic straight lines. And the half-plane on and above line 
is the upper half-plane , and the line is to be its X-axis. The green and red points on the circle C have a common point O. That means The green and red parts on the upper half-plane must have a common point at infinity high up. And that is nothing but a single point. Moreover, the circumference of circle C is a closed loop, and so the straight line is not straight but a part of circle with infinite radius.BR>
[2]: It shows an illustration on an above basis. The infinity can not be drawn nor even think as we have discussed. But we dared to imagine it. We are at the bottom of the circle.
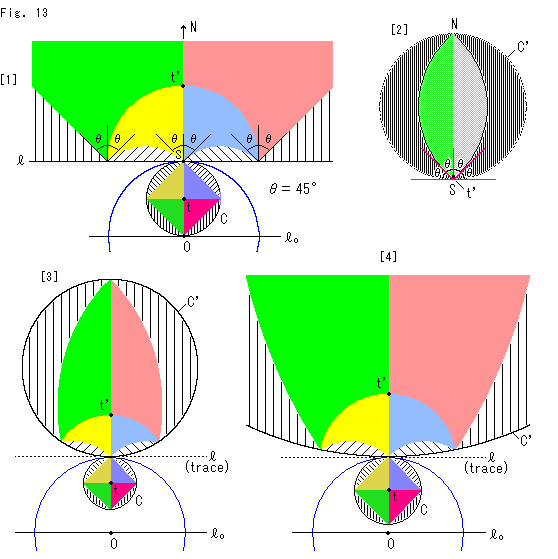
Look at Fig. 13.
We exchanged in the circle C for 
as shown.
[1]: It shows the inversion of every part. Point t is the center of circle C and its inverted point is t'. Point t is the common point of straight line , circle C and inversion circle. The straight line passes the center of inversion circle and is parallel to straight line . Any angle 
is 45
. It is distinctive comparing with Fig. 12.
[2]: Imitating Fig. 12, we illustrated the upper half-plane entirely. The circle C' is drawn regarding the line as a part of circle C' with the infinite radius. We drew arround the top N similarly to the bottom S. Well, is it correct?
[3]: To confirm it we shrank the circle C and spaced it from the center O of inversion circle. An inversion is conformal mapping so that where 45 is 45 and where 90 is 90, no change at all. The dotted line is the trace of . And there appeared the circle C.
[4]: We made the circle C a little. It is similar to [1]. If the circle C continuously gets bigger and it will be [2] when the circle C passes the center O of inversion circle. Therefore, we could say [2] is right.
But in order to regard the circle C' as a circle with infinite radius, we have to define its metric. It should essentially be that of the upper half-plane ,
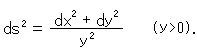
We guess we may set XY-direction like the figure right and apply this metric. But it is out of our hand to calculate it now.
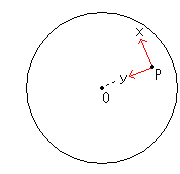
Look at Fig. 14.
We let the radius of inversion circle be 2 and the radius of Poincare disk C be about 0.996. Then, as a construction, we can draw Poincare disk C that looks passing the center O of inversion circle. It is false but we can get circle C' as a closed loop when the disk C is inverted.
[1]: The circle C' is compressed by 1/100 for drawing. Most of inverted points fall in near point S. So we drew straight lines near the center O of inversion circle and inverted them.
[2]: It ia a figure magnified around point O. The inverted curves in circle C' of [1] looks at a glance a homothety of the original curves in circle C. But it is not true. Watch symbols carefully. The gap between the circle C and straight line is what exposed of construction false. Leave it as it is.
[3]: We enlarged around point O of [2] to see red curves.
Well, it does no bear out enough to guess the situation in the circle with C' infinite radius though we have drawn these figures.
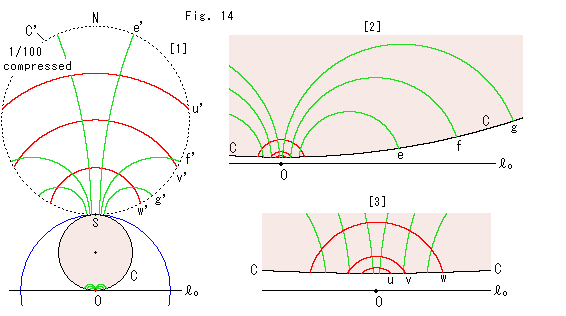
Look at Fig. 15.
We draw an orthogonal lattice on the upper half plane and invert it.
[1]: The lattice is lifted a little. So the inverted lattice stays inside the circle C without touching the circumference.
[2]: It is the circle C enlarged for easy observation. Every corner of any domain is right angled.
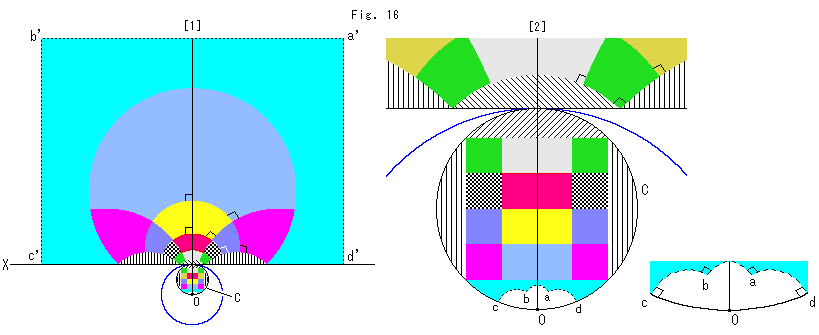
Look at Fig. 16 above.
This time, we draw an orthogonal lattice that fits the circle C exactly.
[1]: The inverted lattice consists of circular arcs each of which is perpendicular to others.
[2]: It is an enlarged copy of the circle C and its neighbor. There are striped patterns and sky blue domain around the lattice. The white area in the circle C consists of four circulsr arcs and corresponds to the outside of the sky blue area above the line X. Corners a, b, c and d correspond to a', b', c' and d' respectively. The dotted line is the border and each corner is right angled as shown right below.
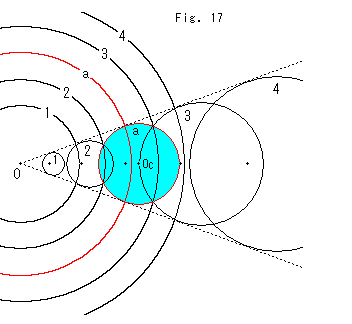
Look at Fig.17.
What will happen if the size of inversion circle alternated? The concentric circles with the center O has equal gaps. They are inversion circle
/////////////////////////////////////////////-*-*/-*/-*/-*-*/-*/-*-*/-*/-*/-*/-*/-*/-/*-*-*/
Fig.18
Fig.18
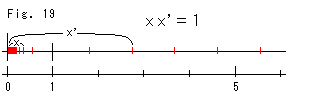
Fig.19
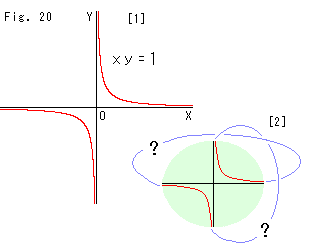
Look at Fig. 7.
Let's think of the end point of a hyperbola since an inversion is a relationship among coordinates of points on the hyperbola.
[1] is an ordinary hyperbola. In this diagram, we feel that the line goes up infinitely, passes through a mysterious zone and reappears at the very bottom. Then it turns left and goes infinitely left. And then it again reappears from the right.
[2] is an imagined route of a man who traveled along the red hyperbola and experienced this mysterious zone. The zone could be a nest of points at infinity.
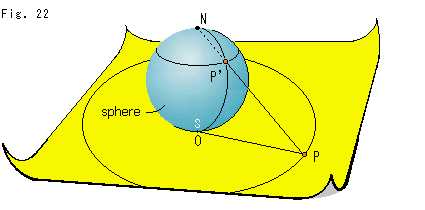
Fig. 8 is a trick illustration.
We open a sheet of paper (plane) and set a sphere with its south pole S at the bottom. The point N on the sphere is the north pole. The bottom is at the origin O on the plane. Points P and P' correspond to each other along the projected line N-P'-P as shown. We can spread the plane wider as point P moves farther from the origin. Then point P' moves up toward the north pole N as point P moves toward infinity. Whatever route and direction point P takes, point P' will arrive at point N if point P arrives at infinity. Suppose the sphere is the plane (point P' is identical to point P) and the north pole N is a point at infinity. Then everything will go well, we hope. Of course, we have to measure distance on the sphere as the distance on the plane. Since we regard point N as a point at infinity, any distance from point N is infinity.
This allows us to understand that a plane is a closed surface of infinitely large size. That means numberless points at infinity on a "plane" become a single point, and one to one correspondence is maintained perfectly. However, on a hyperbola, we guess, the number of points at infinity should be two (separated) rather than one.
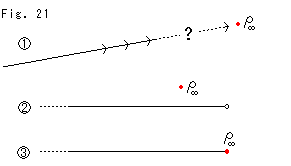
First of all, can we really extend a straight line up to infinity, as depicted in Fig. 9?
Euclid said "the end of a line is a point" and "a segment can be extended as much as we want". He never said "infinitely" but "as much as we want".
Let us temporarily define a straight line in this way:
It is extended unlimitedly but not up to a point
at infinity even if it exists.
(Of course, we are free to imagine a straight
line that extends to the point at infinity.)
There is no gap between a straight line and
the point at infinity but we cannot define the
joint point.
Fig. 9' illustrates this. In a mathematical term a straight line is a so-called line.
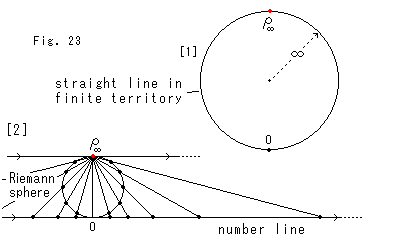
Look at Fig. 10.
[1] is a picture that joints the red point in Fig. 9' and a circle with infinite radius that we regard as a straight line. (Pay no attention to a discussion on the joint point.) This "straight" line is really extended forever. It can go round and round passing even the point at infinity . Here remember that a point at infinity is not always necessary to stay at infinity.
[2] is a popular diagram of correspondence between a number line and a point at infinity . [1] was drawn by force as the whole of [2]. There is no difference whether the circle in [1] is that of [2] or the number line. "?" in Fig. 7 and North pole N in Fig. 8 also looks passable.
Well, there several uncertain things we talked.
Can we really go round the circle with infinite
radius and get back to the start point?
And
when we travel along a number line unlimitedly,
can we really reappear in the opposite direction
via a point at infinity as a stepping-stone?
We have clarified none of these.
A point that stays at infinity exists whatever we do, doesn't it? If we can reappear at the left after we have gone to the right, "direction" makes no sense, doesn't it? To break this deadlock we have to apply techniques of projective geometry. We will see it.