It is said that Lobachevsky and two others finally solved the mystery of parallel lines 2,000 years after Euclid. Why did it take such a long time? It is true that there was a full mind barrier. But, apart from it, people had to wait till the time is ripe. In other words, people before the three had no mathematical tools such as logarithms, differential and integral calculus, and hyperbolic function.
We can see how angle and distance depend on each other by using hyperbolic trigonometry. Why can we get that result with hyperbolic function? Hyperbolic trigonometry had been proven by Lobachevsky himself. What we want to know is not a demonstration or proof. We guess that hyperbolic function has its origin in itself. For example, one riddle we have deals with the ratio of the circumference of a circle to its diameter, namely that it is 3.14 ..., which has been proven. But why is it not 5 or 6? Why is it always the same for a small circle and a large circle? So let's look to hyperbolic function to come up with an explanation.
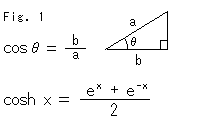
Fig. 1 defines an ordinary cos (cosine) and a cosh (hyperbolic cosine). They say that the latter is quite similar to the former. It seems true if we refer to a book of formulae. But why do they have a similar nature in spite of the fact that the definition looks completely different from each other? Cos is a relation between the ratio of sides (length) b to a of a right-angled triangle and the included angle ![]() as shown in the figure. To what things is cosh related? We cannot understand it at all from the definition, can we?
as shown in the figure. To what things is cosh related? We cannot understand it at all from the definition, can we?
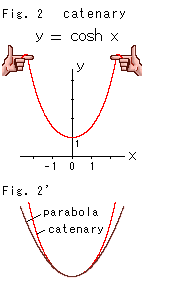
Fig. 2 shows a curve based on the definition of cosh. This red curve is called a catenary. We can easily get it by holding a rope as shown. In the old days, mathematicians had a hard time finding the equation of a curve. Galileo thought it was a parabola. Some people fought hard to prove that the catenary is parabola.
Mathematicians at that time knew only the outline of physical properties of the catenary. Differential and integral calculus were developed around 1670, but there was no symbol for the base e of natural logarithm. In 1691, Johann Bernoulli and some others discovered the expression of catenary. The hyperbolic function was born!
Take a look at Fig. 2'. The catenary is similar to a parabola but not equal. Let's express cosh x and cos x in series and compare the two.
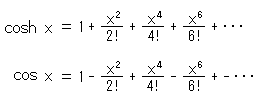
And a parabola can be written as
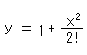
So cosh and the parabola are almost equal at small x. But cosh is not similar to cos though we feel something in common. We can easily find similarities between hyperbolic function and trigonometric function in a book of formulae, but we want to see the true nature of hyperbolic function.
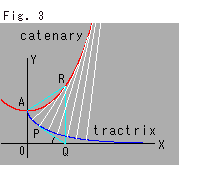
Look at Fig. 3. There is a relation between the catenary and pseudosphere. The red curve is the catenary and the blue curve is a tractrix, which is a generator of the pseudosphere. The white lines are normals that stand on the tractrix. (In the picture, they are at regular intervals along the tractrix.) The envelope of normals forms the catenary and every normal is tangent to the catenary. The catenary is also a locus of the center of an outer osculating circle on the pseudosphere (cf. Chapter 22). Line PQ is tangent to the tractrix. AR = RP, AO = PQ = 1, and straight line QR is perpendicular to the X-axis. There several expressions of the tractrix. They are as follows:
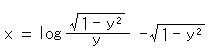
In trigonometric functions
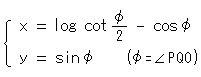
and in hyperbolic functions

where t is a parameter. The parentheses show the definition of tanh (hyperbolic tangent).
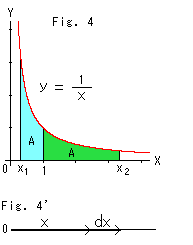
Look at Fig. 4.
Let's look at a hyperbola, since hyperbolic functions are "hyperbolic ---".
The areas of the two colored sections are equally A. The border x = 1 is to make things simple. Then
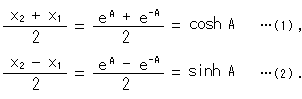
Sinh (hyperbolic sine) in (2) is the definition. Let's see where they come from.
Look at Fig. 4'.
The area S under the red hyperbola y = 1/x is
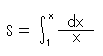
Look at the right side after the integral symbol carefully. It is a ratio of increment dx to length x. Therefore, hyperbolic function can be explained as a proportion of the change in length. Also
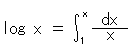
What we should pay attention to is that a logarithm is defined as the integration of the ratio of an increment to its amount rather than an inverse exponent. And
Therefore, area S under the hyperbola is the logarithm of length x of the asymptote, and the length x is exp a. The definition (1) is the mean value of x = ![]() and x =
and x = ![]() . The definition (2) is contrastive to (1).
. The definition (2) is contrastive to (1).
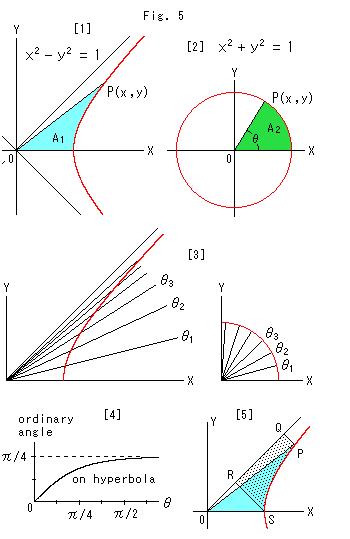 Look at Fig. 5.
Look at Fig. 5.
And parameter t is two times the area of the sky blue area ![]() . That is, t = 2
. That is, t = 2![]() .
.
[2] is a circle with radius 1. It can be described with angle ![]() as
as
Since the radius is 1, angle ![]() is two times greater than the green area. Namely,
is two times greater than the green area. Namely, ![]() = 2
= 2![]() . This resemblance between a circle and a hyperbola was discovered around 1750. If t =
. This resemblance between a circle and a hyperbola was discovered around 1750. If t = ![]() ,
, ![]() =
= ![]() . But angle POX of the hyperbola does not equal angle POX of the circle. We therefore measure angle POX of the hyperbola with parameter t, or we graduate the angle in parameter t. And we describe angle POX of the hyperbola in
. But angle POX of the hyperbola does not equal angle POX of the circle. We therefore measure angle POX of the hyperbola with parameter t, or we graduate the angle in parameter t. And we describe angle POX of the hyperbola in ![]() that is the central angle of the circle. Angle
that is the central angle of the circle. Angle ![]() is called a hyperbolic-angle on a hyperbola and a circular-angle on others. A circular-angle is an ordinary angle.
is called a hyperbolic-angle on a hyperbola and a circular-angle on others. A circular-angle is an ordinary angle.
[3] shows the hyperbolic-angle and circular-angle under this arrangement.
[4] shows the relation between the hyperbolic-angle ![]() and the ordinary angle on the hyperbola. On the circle, the circular-angle
and the ordinary angle on the hyperbola. On the circle, the circular-angle ![]() itself is an ordinary angle.
itself is an ordinary angle.
[5] shows the dotted area surrounded by the asymptote and two perpendicular lines PQ and RS, which is similar to Fig. 4. The area PQRS equals that of the sky blue sector POS wherever point P is located.
Let us rewrite the two formulae above with ![]() .
.
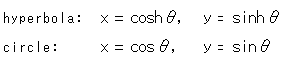
The ![]() in the first formula is a hyperbolic-angle and a parameter. The
in the first formula is a hyperbolic-angle and a parameter. The ![]() in the second formula is a circular-angle and an actual angle. When
in the second formula is a circular-angle and an actual angle. When ![]() is attached to a hyperbolic function, it is a hyperbolic-angle. When the
is attached to a hyperbolic function, it is a hyperbolic-angle. When the ![]() is attached to a trigonometric function, it is a circular-angle.
is attached to a trigonometric function, it is a circular-angle.
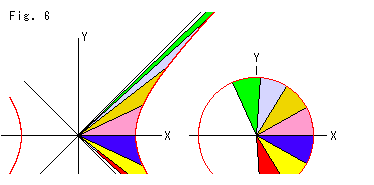
Fig. 6 shows sectors drawn at regular intervals of 0.5 in ![]() . Each sector corresponds to the same colored are in the adjacent drawing. The area of every sector is the same. When
. Each sector corresponds to the same colored are in the adjacent drawing. The area of every sector is the same. When ![]() grows larger, a sector of the hyperbola gets thinner and longer, but sectors on the circle lie one on top of the other (without changing shape), going around like a screw. We can now feel the difference between the inside and outside of the hyperbola, as we did in the case of a circle.
grows larger, a sector of the hyperbola gets thinner and longer, but sectors on the circle lie one on top of the other (without changing shape), going around like a screw. We can now feel the difference between the inside and outside of the hyperbola, as we did in the case of a circle.
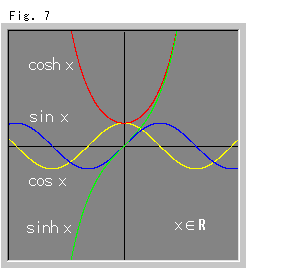
Fig. 7 shows trigonometric functions and hyperbolic functions where x is a real number. A trigonometric function is a periodic function, but a hyperbolic function is not so. For example, cos is not greater than 1, but cosh is not less than 1. However, when we use the imaginary number ![]() with a real number x, we can unite trigonometric functions and hyperbolic functions in this way:
with a real number x, we can unite trigonometric functions and hyperbolic functions in this way:
All of the right sides are real numbers though they contain ![]() . It is also said that a hyperbolic function is a periodic function.
. It is also said that a hyperbolic function is a periodic function.
An imaginary number has been used since the 1400s, but it is still somewhat mysterious even today. For instance, it is not easy to imagine ![]() (
(![]() raised to the
raised to the ![]() power) even if we know function theory. But we do not need to worry about it if we agree that an imaginary number simply indicates one calculation method.
power) even if we know function theory. But we do not need to worry about it if we agree that an imaginary number simply indicates one calculation method.
Fig. 8 shows hyperbolic functions where z is a complex number.
[1]: a = 1 and b = 2 for z = a + ![]() b.
b.
[2]: ![]() is a monotone increasing function but
is a monotone increasing function but ![]() spins.
spins.
[3] to [5]: Certainly hyperbolic functions are periodic functions. They are spinning.
That which lets a hyperbolic function work as shown in Fig. 4 to Fig. 6 is base e of a natural logarithm, isn't' it? That e appeared at the beginning of our story, in the parallel angle formula or Lobachevsky's Postulate (cf. Chapters 7 and 8). We began by accepting that "parallel lines are not straight but curved". Well, we returned the starting point!
The base e of a natural logarithm was discovered by Napier and others around 1619. However, if we go and inquire deeply about this, we will be carried adrift in a mathematical ocean. So, we will change our object of attack.
We will pursue the imaginary number ![]() . Speaking of something that is curved, any diagram of an exponent or a complex number is curved. A complex number usually makes a curve because it is a vector (a pair of two numbers).
. Speaking of something that is curved, any diagram of an exponent or a complex number is curved. A complex number usually makes a curve because it is a vector (a pair of two numbers).
Sin x or cos x, where x is a real number, can be expressed with the imaginary number ![]() as
as
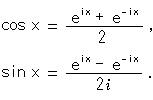
The right sides contain ![]() , but they are real numbers. What we want to pay attention to is that trigonometric functions are described with exponential functions. Why, it might even be a sign of a mechanism! Incidentally, the famous
, but they are real numbers. What we want to pay attention to is that trigonometric functions are described with exponential functions. Why, it might even be a sign of a mechanism! Incidentally, the famous ![]() appears in these two equations.
appears in these two equations.
Let's compare a series of functions (exponent, trigonometry and hyperbola).
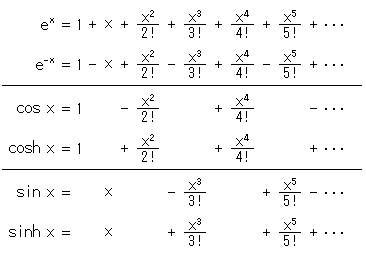
The similarities between the three functions are analytically shown, but they have much to say.
Next, let's look at hyperbolic trigonometry.
Let opposite sides of triangle ABC be a, b and c respectively. Then the law of sine in hyperbolic trigonometry is
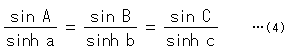
We apply equation (3) to this law. Then it becomes
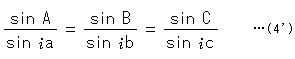
(Common factor -![]() in denominators has been deleted.)
in denominators has been deleted.)
It is the same as law of sine in spherical trigonometry with the exception of ![]() .
.
There are three laws of cosine in hyperbolic trigonometry. One of them is
We apply equation (3) to this law. Then it becomes
It is the same as the law of cosine in spherical trigonometry with the exception of ![]() . Similarly, this situation happens with the other two laws of cosine, changing letters A, B, C and a, b, c cyclically.
. Similarly, this situation happens with the other two laws of cosine, changing letters A, B, C and a, b, c cyclically.
When we combine the three laws of cosine in hyperbolic trigonometry, we get three other fundamental laws. One of them is
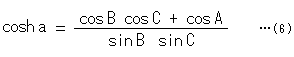
Surprise! It says that "Sides a, b and c are defined by angles A, B and C".
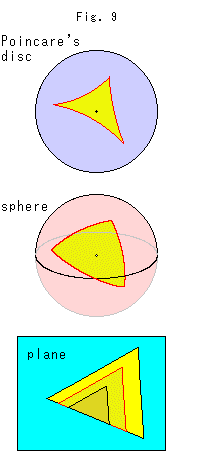
Fig. 9 shows triangles on Poincare's disc, on a sphere and on a plane. We can make similar triangles on the plane, but not on either Poincare's disc or the sphere.
Also, from this equation we see that the sum of the interior angles of a triangle is less than ![]() and the area of a triangle is
and the area of a triangle is ![]() - A - B - C.
- A - B - C.
Applying equation (3) to this equation (6), we get
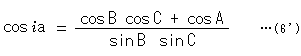
Similarly, this situation happens to cosh b and cosh c. If we remove ![]()
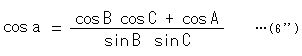
in spherical trigonometry. This law also defines sides a, b and c by angle A, B and C. Contrary to hyperbolic geometry, it concludes that the sum of the interior angles of a triangle is greater than ![]() and the area of a triangle is A + B + C -
and the area of a triangle is A + B + C - ![]() . Hyperbolic geometry is the exact opposite of spherical geometry, isn't it? We are getting the feeling that nothing is surprising in hyperbolic geometry anymore!
. Hyperbolic geometry is the exact opposite of spherical geometry, isn't it? We are getting the feeling that nothing is surprising in hyperbolic geometry anymore!
Thinking on these things, it may seem that hyperbolic geometry is the geometry of the surface of an imaginary sphere. In fact, Lobachevsky named his geometry "imaginary geometry". His "imaginary" meant not only that it utilized imaginary numbers but also that it involves our imagination.
Even so, we cannot yet understand this completely because we guess that an area on the imaginary sphere is negative.
There is another story.
Before hyperbolic geometry was discovered, Lambert found that if the Euclidean parallel axiom is denied, the area S of a triangle ABC would be
where t is a constant depending on unit length.
And he compared it with the area S of a triangle ABC on a sphere with radius r.
Then he guessed that his new geometry stands on an imaginary sphere. To be sure, we feel so, too. Unfortunately, however, he gave up because he judged it inconsistent that the unit length in his new geometry would inevitably be determined if he makes it so that t = 1. A unit length should be chosen freely.
How about the following?
Let's assume that the formula of Gaussian curvature is applicable to an imaginary sphere. Then the curvature of a sphere with radius ![]() is exactly -1. The conclusion is that a hyperbolic plane is an imaginary sphere.
is exactly -1. The conclusion is that a hyperbolic plane is an imaginary sphere.
We have groped our own way toward an understanding of hyperbolic function and imaginary numbers. We can now say that the origin of the mechanism of hyperbolic geometry is exponential function, particularly ![]() where z is a complex number. We know intuitively that it is a curved space. Visualization is not yet complete, however.
where z is a complex number. We know intuitively that it is a curved space. Visualization is not yet complete, however.