Hyperbolic Non-Euclidean World
Ch. 33 Dodecahedron 
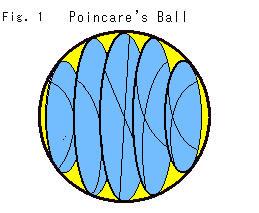
We have treated only 2-D Hyperbolic Non-Euclidean World. What will happen in 3-D world? Here we think of it with an extended-to-3D Poincare's disc model, or Poincare's Ball model. Of course, the ball is open and its hyperbolic radius is infinity.
Look at Fig. 1. The ball is vertically sliced. Hyperbolic planes that look like dishes or bowls are drawn. They are hyperbolic planes though being bent. Every edge of the plane is perpendicular to the ball surface.
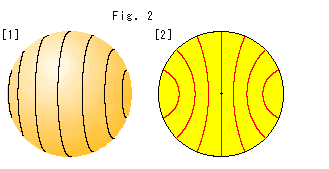
Look at Fig. 2.
[1] is the outward appearance of ball. Black lines are the edges of bent discs.
[2] is the cross section of ball cut through the center. Red lines are cross sections of the planes.
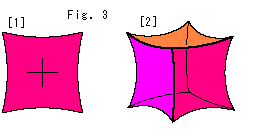
Look at Fig. 3.
[1] is a square drawn in Poincare's disc. We can not tile the disc with it.
[2] is a cube in the ball. Every corner is sharpened. We can not lay it like brick layer in the ball.
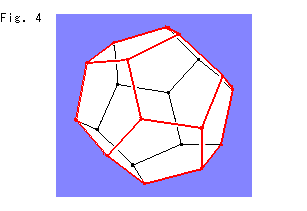 Fig. 4 is an ordinary regular dodecahedron. It consists of twelve pentagons, twenty vertexes and thirty edges, and every dihedral angle is 116.565
Fig. 4 is an ordinary regular dodecahedron. It consists of twelve pentagons, twenty vertexes and thirty edges, and every dihedral angle is 116.565 . And every pentagon has a parallel pentagon (opposite face) that is twisted one-tenth of revolution. Let us fill the ball with dodecahedra. It is not easy for us to image building such blocks without any gap. But in the Hyperbolic Non-Euclidean World it is possible. We may call it a 3-D tiling.
. And every pentagon has a parallel pentagon (opposite face) that is twisted one-tenth of revolution. Let us fill the ball with dodecahedra. It is not easy for us to image building such blocks without any gap. But in the Hyperbolic Non-Euclidean World it is possible. We may call it a 3-D tiling.
The system is as follows.
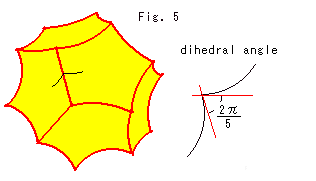
Look at Fig. 5. When we put a dodecahedron into the Hyperbolic Non-Euclidean World, every vertex will be sharpened and dihedral angle gets smaller as shown. Locate the dodecahedron in the center of the Ball, and adjust its size so that the dihedral angle is exactly 2 /5 (72
/5 (72 ). By using this dodecahedron, we can make 3-D tiling. Every edge is surrounded by five dodecahedra. Needless to say, you need infinite number of dodecahedra to fill the Ball fully.
). By using this dodecahedron, we can make 3-D tiling. Every edge is surrounded by five dodecahedra. Needless to say, you need infinite number of dodecahedra to fill the Ball fully.
If we make a dodecahedron with 90 dihedral angle, four dodecahedra have a common edge. Such dodecahedron is called a right-angled dodecahedron. If 60
dihedral angle, four dodecahedra have a common edge. Such dodecahedron is called a right-angled dodecahedron. If 60 dihedral angle, six dodecahedra have a common edge. Such dodecahedron is called an ideal dodecahedron, and all vertexes come to the surface of the Ball model.
dihedral angle, six dodecahedra have a common edge. Such dodecahedron is called an ideal dodecahedron, and all vertexes come to the surface of the Ball model.
Fig. 6 below is 3-D tiling with dodecahedra. Every dihedral angle is 72 . After putting the base dodecahedron (sky blue) in the center of the ball, we piled up to three shells (layers). The first shell (red) contains 12 dodecahedra, the second shell (white) contains 144 dodecahedra. And the third shell (blue) contains 1728 dodecahedra. We are now observing about half of them. Pictures [1], [2] and [3] are views we look around from the center of ball.
. After putting the base dodecahedron (sky blue) in the center of the ball, we piled up to three shells (layers). The first shell (red) contains 12 dodecahedra, the second shell (white) contains 144 dodecahedra. And the third shell (blue) contains 1728 dodecahedra. We are now observing about half of them. Pictures [1], [2] and [3] are views we look around from the center of ball.
[1] is a view right above us.
[2] is a view in front of us.
[3] is a view in the right of us. The left view is symmetrically the same.
[4] is one of dodecahedra looked from outside the ball model.
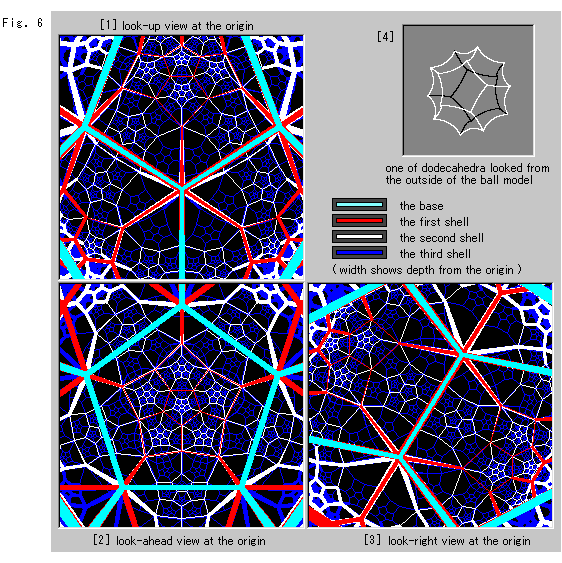

Fig. 7 is an ideal dodecahedron with 60 dihedral angle. Their edges look curved. However, when we, together with our heart, get into the ball, we will find all edges are straight.
dihedral angle. Their edges look curved. However, when we, together with our heart, get into the ball, we will find all edges are straight.
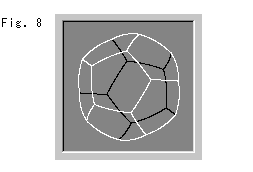
Look at Fig. 8. If it is possible for natives in the ball to see our ordinary dodecahedron in the outside of their world, what they observe is probably a bulgy one as shown.

Look at Fig. 9 right. Inside the Ball, when we move back enough from [2] in Fig. 6, a scene in front of us looks as shown.

Fig. 10 is an artistic composition of Charlie Gunn. It is 3-D tiling of a right-angled dodecahedron. Isn't it attractive? Compare it with Fig. 6 carefully. They look similar to each other, but not the same.
In web Sascha Rogmann opens animation of 3-D tiling
[Back] [Next] [Contents]


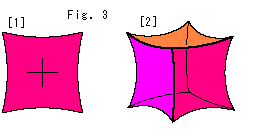
 Fig. 4 is an ordinary regular dodecahedron. It consists of twelve pentagons, twenty vertexes and thirty edges, and every dihedral angle is 116.565
Fig. 4 is an ordinary regular dodecahedron. It consists of twelve pentagons, twenty vertexes and thirty edges, and every dihedral angle is 116.565




