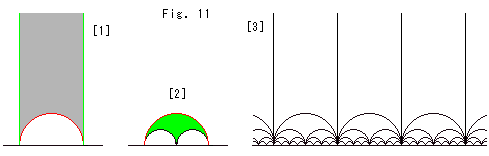Hyperbolic Non-Euclidean World
Ch. 34 Ideal Tetrahedron 
What will happen if we make 3-D tiling with ideal regular tetrahedron?
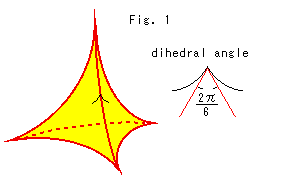
Look at Fig. 1.
All edges of the ideal tetrahedron extend to the surface of the ball model. The dihedral angle of an ordinary regular tetrahedron is 70.517
, but in Poincare's ball model it is exactly 2
(=60). Six regular tetrahedr can perfectly surround an edge. There is no other tetrahedron that fills the ball without any gap. Because we can not choose other dihedral angle by changing the zise of tetrahedron. It is due to the fact that the dihedral angle of tetrahedron is less than 70.517 in the ball, and we can not do like dodecahedron.
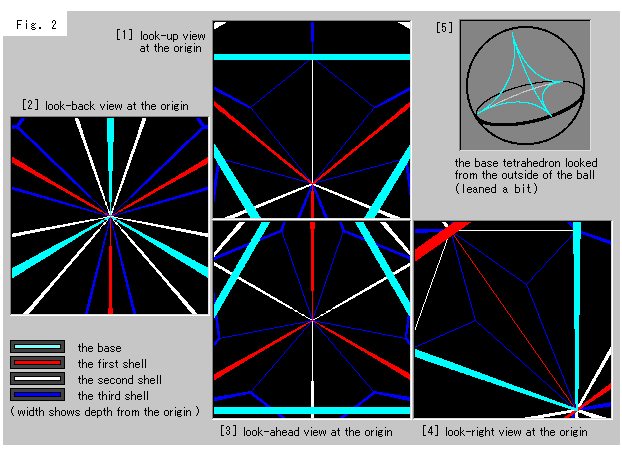
Look at Fig. 2 below. [1] to [4] are views from the ball center. The procedure is much the same as that of dodecahedron.
[1] is a view right above us.
[2] is a view in front of us.
[3] is a view in rear of us.
[4] is a view in the right of us. The left view is symmetrically the same.
[5] is one of tetrahedra looked from outside of the ball. It is tilted a little for easy to observe.
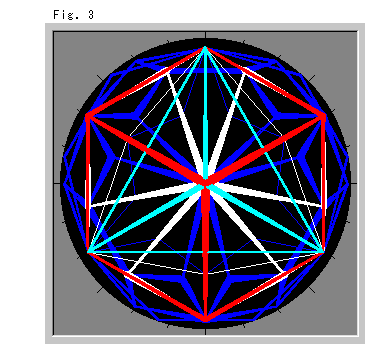
Look at Fig. 3 right. It is the entire ball but tetrahedra were drawn as if an observer is inside. That is, all edges are straight.
About an ideal vertex:
An ideal vertex is a vertex that extends to infinity. However, it is said that an ideal vertex is truly a fiction because all models are open. If so, how should we understand the situation around the line at infinity in projective geometry?
Well, let us have a choice of existence or non-existence for our convenience. And we keep it in mind that an ideal vertex may or may not be fictional point. In most cases, however, we do not need to worry about.
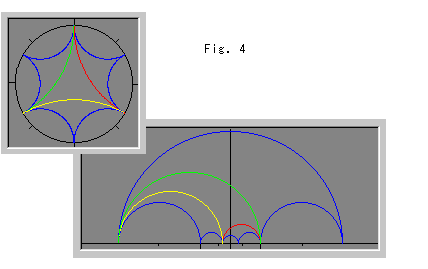
Look at Fig. 4. Let us use an ideal triangle instead of an ideal tetrahedron, and see Poincare's disc (left top) and the upper half-plane (right bottom). The blue curves in the disc are inverted triangles of the central triangle colored in red, yellow and green with respect to its edges. The central triangle corresponds to the base polyhedron in 3-D tiling and three blue triangles correspond to the first shell. Curves in the upper half-plane correspond to those of the disc.
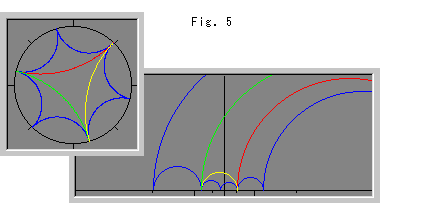
Fig. 5 shows triangles in the disc are turned a little. Triangles in the upper half-plane look much changed.
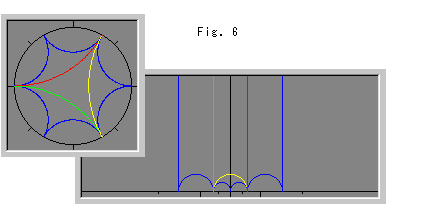
Fig.6 shows that two sides of each triangle in the upper half-plane stretch up to upper infinity.
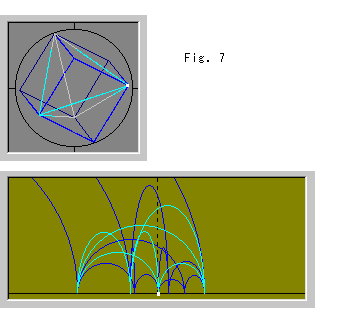
Now 3-D world.
Look at Fig. 7. The top is Poincare'S ball model and the bottom is the upper half-space viewed horizontally. The ball contains an ideal tetrahedron and a cube. The cube consists of the base tetrahedron and four tetrahedra of the first shell. These tetrahedra exactly form the cube. Every edge is drawn in a straight line as if we are inside in the ball. Dark colored area is beyond the vertical plane (curtain) that passes the center of the ball.
The upper half-space is a space that X-axis of the upper half-plane is replaced by a horizontal plane. The white spot is a vertx corresponded to that of the disc. Six sky blue arches and twelve blue arches are drawn.
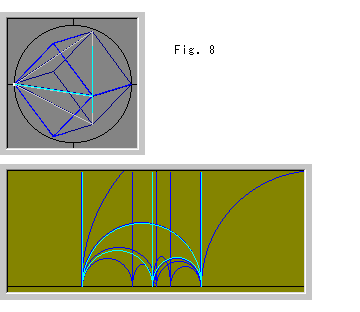
Look at Fig. 8. The location of tetrahedra in Poincare's ball is changed. In this case we can not find the corresponded white spot in the upper half-space due to that it have gone up to upper infinity.
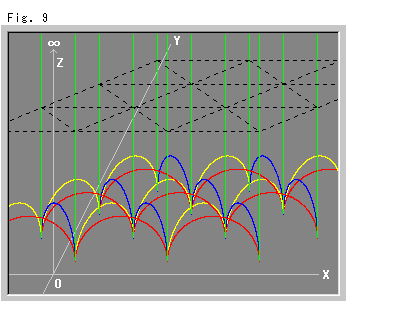
Fig. 9 shows the upper half-space where ideal tetrahedra are laid. Every one of them is drawn as a triangular prism with spherical bottom. The black dotted net is just for our observation. If a tetrahedoron has no ideal vertices, its downward edges are floated (Z>0) from the floor (Z=0).
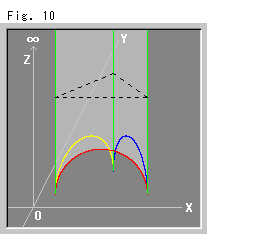
Fig. 10 is a tetrahedron in slight colored for easy to see.
Look at Fig. 11 below. We can fill under the bottom of tetrahedron in Fig. 10 with other tetrahedra. We substitute an ideal triangle for the tetrahedron for easy observation and use the upper half plane.
[1] is an ideal triangle in the upper half-plane.
[2] is an ideal triangle that fits the bottom of triangle [1].
[3] is ideal triangles that inserted under the triangle [1] next to next. This is two-dimentional tiling that corresponds to 3-D tiling.
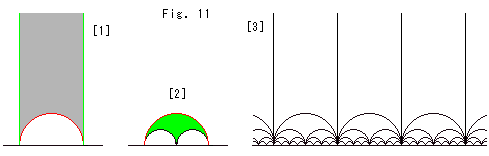
In web there are beautiful ideal polyhedra.
[Back] [Next] [Contents]
(Next is Part 3)