Ch. 35 Projective Geometry (1) 
It is likely that we have to ask help of projective geometry. Riemann's idea was that hyperbolic geometry is a geometry that is obtained by intentional selection of metric or curvature. We can not feel the inevitable in his way for the hyperbolic geometry. Lobachevsky's idea seems to make us feel the inevitable but it is together with some mysterious factors for us.
It is said that we shall naturally find the Hyperbolic Non-Euclidean world in projective geometry. And we need not to distinguish infinity from finiteness. Is that true? What is projective geometry? Let us look at it for the first.
Let us go back to the Euclidean world, and forget about the Hyperbolic Non-Euclidean world for the time being. Then we will try to see infinity with pictures as usual.
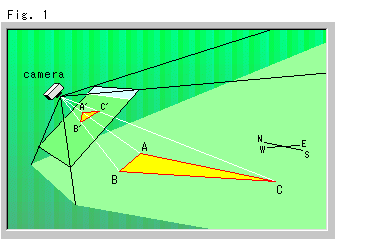
Look at Fig. 1. The camera is the projection center and takes the picture of triangle ABC on the ground. This ground is supposed to be a perfect plane (the earth is flat). The light green area is the view from the camera. Black rays from the camera indicate stereo area (pyramid) of the viewfinder. The square board fitted to black rays is to show what we can look through the camera. Let us call the square board Panel-screen. The photo of triangle ABC on the ground is taken as triangle A'B'C' on Panel-screen. White rays are projective linens of vertices of triangles.
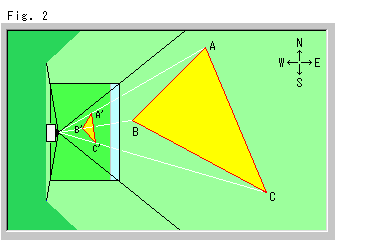
Fig. 2 is a bird's-eye view of the situation in Fig. 1. It shows the correct shape of triangle ABC on the ground. Arrows of north, south, east and west are also just as the picture. But Panel-screen is still slanted and so is the triangle A'B'C'.
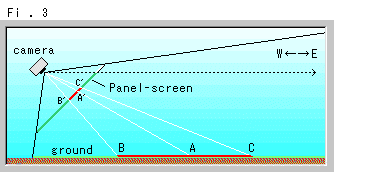
Fig. 3 is the side view of the situation in Fig. 1. The black dotted line indicates the direction of horizon that we can see through the viewfinder of camera.
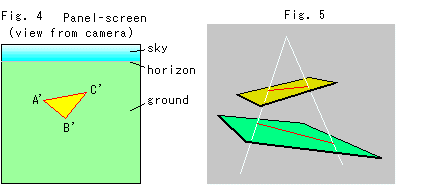
Fig. 4 is the front view of Panel-screen with triangle A'B'C'. The size and shape (interior angles and length of sides) of triangle A'B'C' are different from those of the actual triangle ABC shown in Fig. 3. But triangle A'B'C' is certainly a triangle. That is, a straight line remains as straight.
Fig. 5 explains why a straight line is unchanged by projective transformation. It is self-evident, isn't it?
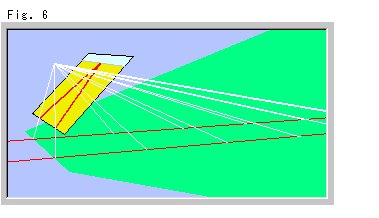
Fig. 6 is a projection of parallel lines. For easy to see, the camera etc. are omitted, and the ground color of Panel-screen is in yellow. The parallel lines on Panel-screen look to have end points and meet each other at horizon .
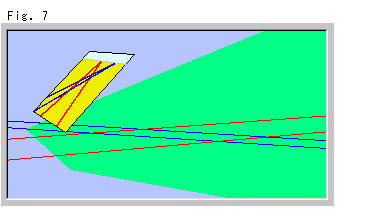
Look at Fig. 7. We drew two pairs of parallel lines on the ground and projected them to Panel-screen. Projective rays are omitted. The blue prallel lines also meet each other at horizon.
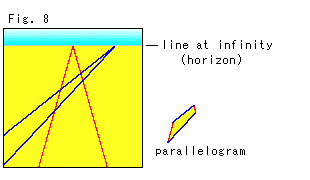
Fig. 8 shows the two pairs of parallel lines on Panel-screen. The lower right is the parallelogram formed by them. Mathematicians call the horizon on Panel-screen a line at infinity. However, there is no such physical line exists. This naming is unsuitable very much. It confuses beginners. It is not a line that exists at infinity. We can catch it only on the Panel-screen as the border of the ground and sky. In other words;
The line at infinity is a man-made product.
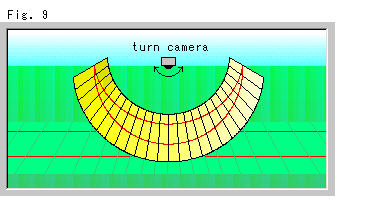
Fig. 9 shows 180
camera shoot with many rectangular Panel-screens. The chained Panel-screens form a half cylinder. It helps us to take a full picture of the entire range of parallel lines. Parallel lines on the ground look like a railroad, but not on chained Panel-screens.
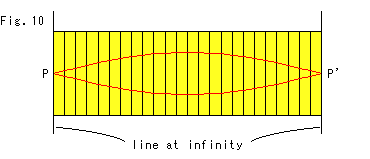
Fig. 10 shows unrolled Panel-screens of Fig. 9. Points P and P' are on line at infinity (horizon). The chained Panel-screens is panoramic and good to see a pair of parallel lines. But it is not convenient for parallel lines with a big gap. And it can not cover straight lines in different direction.
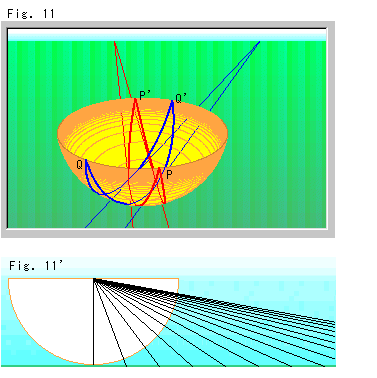Fig. 11 shows two pairs of parallel lines on a sphere. They are projected from the ground to a hemisphere instead of the chained Panel-screens. The center of hemisphere is the projection center. The hemisphere can be considered as that it consists of infinite number of micro Panel-screens (tangent planes). The edge (circumference of the equator) of hemisphere is now a line at infinity.
Fig. 11' shows the longitudinal section with rays through the center of hemisphere in Fig. 11. The rays are from points at regular intervals on the ground. The left area and rays gettig horizontally are omitted.
Now let us regard the hemisphere as a plane and think of a geometry on it. The great circle is naturally considered as a straight line. However, we have a problem. In Euclidean geometry two points defines only one straight line. Two red straight lines reach the two points P and P', and two blue lines reach the two points Q and Q'. It does not fit for the geometry we are used to. Riemann helped us. All we have to do is to identify point P with point P', and point Q with point Q'.
OK. Let us accept it anyway. But, what plane is it? How can we join point P to point P', and Q to Q' at a time without wrapping over? It is physically impossible to make such joints. however, we, human being, can imagine it. It is called projective plane. We hear a voice, "It's outrageous that you talk geometry with imagination." But let us go on any way because the edge of hemisphere is infinity at any rate.
[Back] [Next] [Contents]