
Ch. 46 Projective Transformation and Mobius Transformation 
Projective Transformation changes a straight line into a straight line. So it is a linear transformation. It can be expressed with matries. In homogeneous coordinates it is;
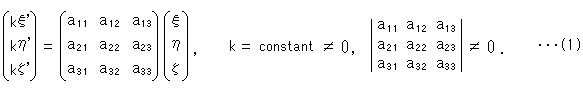

This formula (1) shows a change of a single point ( ,
,  ,
,  ). If the point has nothing to do with other points, k is indeterminate. But k shall be determined if the point has a relation to, for example, congruence.
). If the point has nothing to do with other points, k is indeterminate. But k shall be determined if the point has a relation to, for example, congruence.
The number of elements  is nine. But it is actually eight because we can devide all elements by one of nonzero elements, which becomes 1. Even so, we can not see what the matrix of
is nine. But it is actually eight because we can devide all elements by one of nonzero elements, which becomes 1. Even so, we can not see what the matrix of  tells us. Moreover, we do not know how to find the value of k though we have understood the meaning of it. Let us see it gradually.
tells us. Moreover, we do not know how to find the value of k though we have understood the meaning of it. Let us see it gradually.
rule
/////////////////////////////////////////////////////////////////////////////////////
Let us define the congruence.
If two figures A and B have identical size and shape so that they may be exactly superimposed, we say they are congruent. But their location or measuring instruments could be different from each other. When figure A is moved for the superimposition, doesn't its size or shape change? We have to decide whether A and B are congruent or not even if they are separated.
We say figures A and B are congruent if they change into one another by projective transformation. We do not care how they look to our eyes before or after the transformation. In other words, a figure that moved by projective transformation is congruent regardless its location and shape.
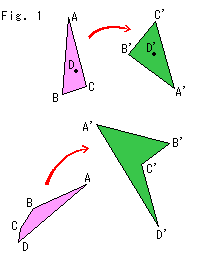 Look at Fig. 1.
Look at Fig. 1.
They are examples of figures moved by projective transformation. Let us determine elements  of transformation matrix.
of transformation matrix.
The elements of an ordinary 3x3 matrix are definitely determined if three points not on a straight line are given before and after transformation. But in homogeneous coordinates four points are to be given before and after transformation because point ( ,
,  ,
,  ) and point (k
) and point (k , k
, k , k
, k ) are the identical. (k is a nonzero constant.)
) are the identical. (k is a nonzero constant.)
Suppose points 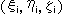 and
and 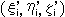 , i = 1, 2, 3, 4, are given before and after transformation respectively, elements
, i = 1, 2, 3, 4, are given before and after transformation respectively, elements  of transformation matrix in (1) will be fixed as;
of transformation matrix in (1) will be fixed as;
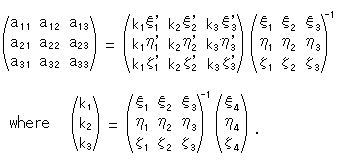 Granted. But the number of elements is nine, that's too many for us to handle.
Granted. But the number of elements is nine, that's too many for us to handle.
We previously constructed Klein disk from imaginary sphere. It was based on the fact that
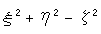 is invariable. Let us apply it to projective transformation (1). Then the elements
is invariable. Let us apply it to projective transformation (1). Then the elements  are limited as;
are limited as;
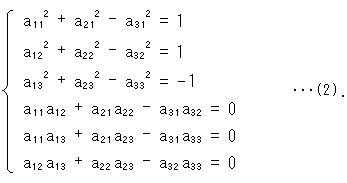
It looks so tight. But projective transformation on condition (2) forms group. Becase whatever elements  are, they forms a regular matrix. It guarantees that cross ratio is invariable even after conditioned (2).
are, they forms a regular matrix. It guarantees that cross ratio is invariable even after conditioned (2).
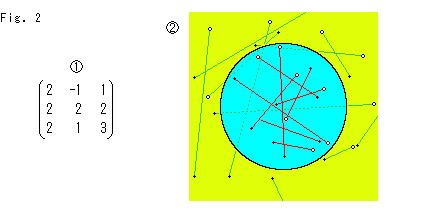 Look at Fig. 2.
Look at Fig. 2.
 : It is an example of transformation matrix with condition (2). We can make many matrixes like this, but it is hard for us to find any common peculiarity of them.
: It is an example of transformation matrix with condition (2). We can make many matrixes like this, but it is hard for us to find any common peculiarity of them.
 : However, the condition (2) results that inside points of Klein disk never go outside, and outside points never get into the inside. In the figure points are given randomly and each point is moved by matrix that is chosen randomly. Lines are drawn between two points, one is given and another is after transformation. The lines are not loci but show connection of each transformation. Both end points of every red segment are inside of Klein disk, and those of every green segment are outide of the disk. A point on the circumference can move only on the circumference.
: However, the condition (2) results that inside points of Klein disk never go outside, and outside points never get into the inside. In the figure points are given randomly and each point is moved by matrix that is chosen randomly. Lines are drawn between two points, one is given and another is after transformation. The lines are not loci but show connection of each transformation. Both end points of every red segment are inside of Klein disk, and those of every green segment are outide of the disk. A point on the circumference can move only on the circumference.
**************************************************
Let us leave the above as it is, and think about upper half plane  . Because projective transformation has so many elements that we feel difficulties, and the action of projective transformation should appear on a model we are familiar with.
. Because projective transformation has so many elements that we feel difficulties, and the action of projective transformation should appear on a model we are familiar with.
A figure on upper half plane  is moved by Mobius transformation;
is moved by Mobius transformation;
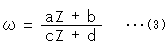 provided that
provided that
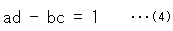
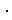
a, b, c and d are real number. Z and  are complex number. ( (3) is also called "linear transformation". But we do not use it to avoid confusing with projective transformation that is linear.)
are complex number. ( (3) is also called "linear transformation". But we do not use it to avoid confusing with projective transformation that is linear.)
Mobius transformation forms group, too. Because Mobius transformation can be expressed with a matrix;
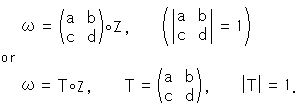
Symbol " " indicates formula (3). When we make Mobius transformation n times continuously, all we have to do is to make n-th power of the matrix,
" indicates formula (3). When we make Mobius transformation n times continuously, all we have to do is to make n-th power of the matrix, 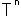 . Isn't it convenient?
. Isn't it convenient?
The elements a, b, c and d can be determined by three points before and after the transformation (6 points in all).
It is agreeable. But it is not easy for us to calculate them if the elements are limited as real number. Therefore, we leave that the elements are to be given and points are to be moved by Mobius transformation.
We have not paid much attention to that the movement of a point is tied to such transformation. It was enough that we have known a hyperbolic straight line appears as a semicircle and how to measure its length. But now, we are going to see the root of the movement.
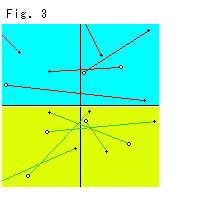 Look at Fig. 3.
Look at Fig. 3.
Verious points on an ordinary plane are moved by Mobius transformation (3) with condition (4). A Mobius transformation is randomly chosen for each point. A point above X-axis (Y > 0) moves only above X-axis, and a point only below X-axis (Y < 0) moves only below X-axis. A point on X-axis moves only on X-axis. It never get out of X-axis. These movements correspond to Fig. 2, isn't it?
The expression, we often see, "upper half plane  is transferred to its own" means that any point on upper half plane can move only on the upper half plane.
is transferred to its own" means that any point on upper half plane can move only on the upper half plane.
We can draw the same figure by using projective transformation (1) if we replace condition (2) by
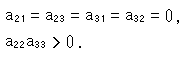
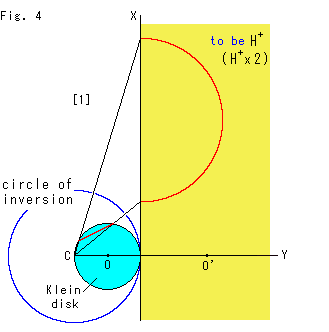 Look at Fig. 4.
Look at Fig. 4.
It is easy to connect upper half plane  to Klein disk. We have drawn it before, but here we use a circle of inversion for drawing.
to Klein disk. We have drawn it before, but here we use a circle of inversion for drawing.
The small sky blue disk O is Klein disk. Its left end is at the center C of the blue inversion circle. Klein disk is changed into the yellow half plane that is infinitely wide. This half plane is twice as large as the actual upper half plane  . So keep it in maind when you see this diagram. Point O' corresponds to the center O of Klein disk. Since a circle that passes the center of inversion circle becomes a straight line, the circumference of Klein disk is X-axis (vertical line) now. The red chord on Klein disk is a hyperbolic straight line and is now the red semicircle on the yellow half plane.
. So keep it in maind when you see this diagram. Point O' corresponds to the center O of Klein disk. Since a circle that passes the center of inversion circle becomes a straight line, the circumference of Klein disk is X-axis (vertical line) now. The red chord on Klein disk is a hyperbolic straight line and is now the red semicircle on the yellow half plane.
Thus Klein disk becomes the half plane. Accordingly, projective transformation (1) with condition (2) should be replaced by Mobius transformation (1) with condition (2).
Then, it is enough for us to see
4 letters a,b,c,d and a single condition (4)
instead of
9 letters 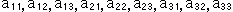 and 6 coditions (2).
and 6 coditions (2).
In other words, what we have seen on the upper half plane  was what projective transformation (1) with condition (2) performed. It's OK, but it is not easy to formulate the relation between
was what projective transformation (1) with condition (2) performed. It's OK, but it is not easy to formulate the relation between  and a,b,c,d. This diagram shows the situation when the formula is applied.
and a,b,c,d. This diagram shows the situation when the formula is applied.
In Mobius transformation it is easy to make a formula with condition (4).
First, let Z and  be
be
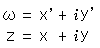
And we divide Mobius transformation into real and imaginary conponents:
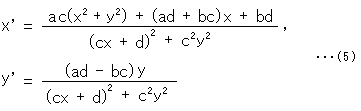

Both y and y' will simultaneously have same signs if ad - bc = 1 is substituted to (5). In short it becomes like Fig. 3.
Here below let ad - bc = 1 .
If a is not zero, let a be 1. Then d = 1 + bc, and
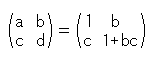
 And
And
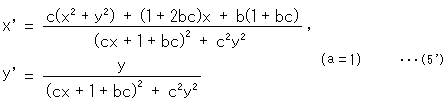
 Condition (4) is met whatever b and c now.
Condition (4) is met whatever b and c now.
If a = 1 and c = 0, then x' = x + b, y' = y, and  shifts only right or left.
shifts only right or left.
If a is allowable to be zero,
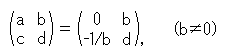 and
and
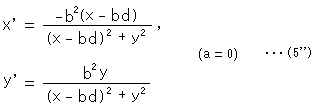
 b (
b (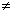 0) and d can be any value now.
0) and d can be any value now.
Formula (5'') is a formula of inversion except that x and x' are different signs. The inversion circle has its center at point (bd, 0) and radius of |b|.
Let us see how Mobius transformation works.
There are two methods.
Fixed-abcd method: fix a, b, c and d, and change Z,
and
Fixed-Z method: fix Z, and change a, b, c or d.
 is moved by either method. (Naming of methods is just for convenience of explanation.)
is moved by either method. (Naming of methods is just for convenience of explanation.)
 We adopt Fixed-abcd method, and apply Mobius transformation with condition (4) to an ordinary plane. We regard the lower half plane is a mirror copy of the upper half. We do not care about the upper half plane
We adopt Fixed-abcd method, and apply Mobius transformation with condition (4) to an ordinary plane. We regard the lower half plane is a mirror copy of the upper half. We do not care about the upper half plane  at this moment. We use different color on the upper and lower just for illustration.
at this moment. We use different color on the upper and lower just for illustration.
Look at Fig. 5.
We move point Z on a straight line.
 : None of a, b, c or d is zero. Straight line Z becomes circle
: None of a, b, c or d is zero. Straight line Z becomes circle  . The dotted lines connect corresponding points. These dotted lines never go across X-axis. The arrows show corresponding directions when Z starts from X-axis. A corresponding point
. The dotted lines connect corresponding points. These dotted lines never go across X-axis. The arrows show corresponding directions when Z starts from X-axis. A corresponding point  on the red circle gets back to X-axis again when point Z on the blue straight line goes far to infinity.
on the red circle gets back to X-axis again when point Z on the blue straight line goes far to infinity.
 : Only c is zero. Straight line Z becomes straight line
: Only c is zero. Straight line Z becomes straight line  . Z and
. Z and  move in the same direction. They are always in parallel.
move in the same direction. They are always in parallel.
 : a, b, c and d are similar to those of
: a, b, c and d are similar to those of  . To tell the truth, Z and
. To tell the truth, Z and  are in similarity whatever Z is. In hyperbolic geometry there is no similarity, of course. But this plane is the Euclidean plane. The design Z has no meaning at all.
are in similarity whatever Z is. In hyperbolic geometry there is no similarity, of course. But this plane is the Euclidean plane. The design Z has no meaning at all.
 : Only a is zero. In this case straight line Z becomes red circle
: Only a is zero. In this case straight line Z becomes red circle  , too. But circle
, too. But circle  nust pass the origin. When point
nust pass the origin. When point  on the circle gets back to the origin, point Z on the straight line goes far to infinity. Arrows are similar to
on the circle gets back to the origin, point Z on the straight line goes far to infinity. Arrows are similar to  .
.
 shall form a circle whenever Z is a straight line unless c is zero.
shall form a circle whenever Z is a straight line unless c is zero.
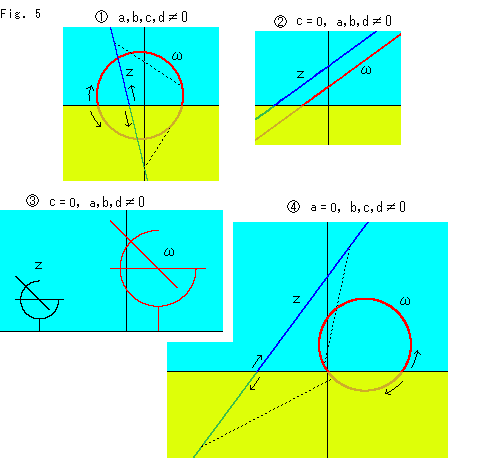
Look at Fig. 6.
We move point Z on a circumference. None of a, b, c or d is zero.
 : This figure is made with the matrix that is a product of three matrixes;
: This figure is made with the matrix that is a product of three matrixes;
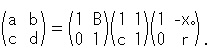 We finalize the matrix that meets ad - bc = 1 by multipling with an appropriate constant, of course. B is a constant. Xo is a distance between the center of circle Z and the origin. r is the radius of circle Z.
We finalize the matrix that meets ad - bc = 1 by multipling with an appropriate constant, of course. B is a constant. Xo is a distance between the center of circle Z and the origin. r is the radius of circle Z.
//////////////////////////////////////////////////////////////////////////////
 is a red vertical straight line now. A matrix can be decomposed into some products of matrixes. One of decomposed matrixes we used was
is a red vertical straight line now. A matrix can be decomposed into some products of matrixes. One of decomposed matrixes we used was 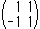 . The matrix (Mobius transformation) changes a circle centered at the origin with radias 1 into Y-axis that is a straight line. The center of circle Z is on X-axis. It is transferred to the red spot on X-axis.
. The matrix (Mobius transformation) changes a circle centered at the origin with radias 1 into Y-axis that is a straight line. The center of circle Z is on X-axis. It is transferred to the red spot on X-axis.
 : c
: c  a now. A circle becomes a circle. The dotted line connects one of pairs of corresponding points. The black spot is the center of circle Z. It is trasferred to the red spot. This red spot is not Euclidean center of circle
a now. A circle becomes a circle. The dotted line connects one of pairs of corresponding points. The black spot is the center of circle Z. It is trasferred to the red spot. This red spot is not Euclidean center of circle  . A circle is transferred to a circle but the transferred center is not the center of transferred circle.
. A circle is transferred to a circle but the transferred center is not the center of transferred circle.
Suppose the plane above X-axis is the upper half plane  and circle Z is a hyperbolic circle. The tiny black star "*" is the location of the hyperbolic center of hyperbiolic circle Z. The black star "*" is transferred to the red star "*" by Mobius transformation. Circle
and circle Z is a hyperbolic circle. The tiny black star "*" is the location of the hyperbolic center of hyperbiolic circle Z. The black star "*" is transferred to the red star "*" by Mobius transformation. Circle  is a hyperbolic circle just as it is. Circle
is a hyperbolic circle just as it is. Circle  does not change even if Z is a hyperbiolic circle. When a figure is moved by Mobius transformation, it does not change for our eyes whether we draw on the upper half plane
does not change even if Z is a hyperbiolic circle. When a figure is moved by Mobius transformation, it does not change for our eyes whether we draw on the upper half plane  or not. The difference between an ordinary plane and the upper half plane
or not. The difference between an ordinary plane and the upper half plane  is only measurement. That is why center * is shifted from center
is only measurement. That is why center * is shifted from center  .
.
 : Ciercle Z straddles X-axis. So does circle
: Ciercle Z straddles X-axis. So does circle  . The transferred center is not the center of circle
. The transferred center is not the center of circle  , too.
, too.
Next we adopt Fixed-Z method. This time we will see how Mobius transformation works on upper half plane  .
.
Let us make a special agreement to apply Mobius transformation onto upper half plane  . Usually we should not divide any number by zero. But here we do:
. Usually we should not divide any number by zero. But here we do:
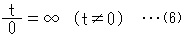

If you do not agree with this (6), think it as a limit 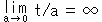 . We may take the symbol "
. We may take the symbol " " for an infinity or a point at infinity, either will do. We do not care whether it positive or negative, or we choose either of them for convenience.
" for an infinity or a point at infinity, either will do. We do not care whether it positive or negative, or we choose either of them for convenience.
A hyperbolic plane model is open. How does it fit for the above agreement? Well, let us see it later and pass over it now.
Let fixed Z be a circle. ( must become a circle if Z is a circle, provided that a straight line is a circle with infinite radius.)
must become a circle if Z is a circle, provided that a straight line is a circle with infinite radius.)
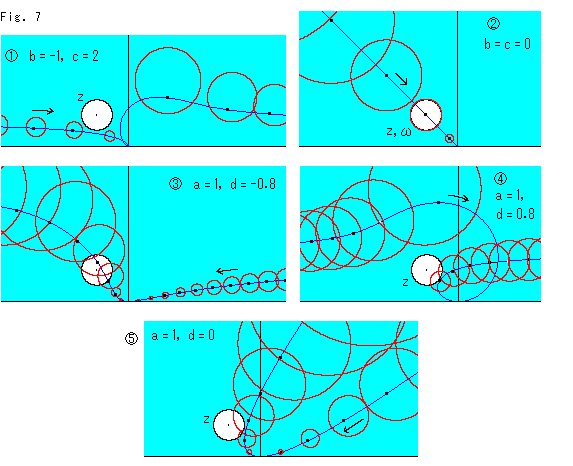 Look at Fig. 7.
Look at Fig. 7.
a and d are fixed and we change b while keeping c = (ad - 1)/b. (b can be zero). A circle will be a horocycle if its center is on X-axis. Therefore we put the circle Z above X-axis.
 : Red circles are
: Red circles are  . The blue line is locus of its center. The arrow indicates the direction of locus when b get bigger. The locus passes the origin (foot of the imaginary-axis) when b is zero. c is infinity
. The blue line is locus of its center. The arrow indicates the direction of locus when b get bigger. The locus passes the origin (foot of the imaginary-axis) when b is zero. c is infinity  and circle
and circle  becomes a point at the moment.
becomes a point at the moment.
The size of circle  looks to chage but it is not true. All circles
looks to chage but it is not true. All circles  are the same in size. The plane we are using now is not an ordinary plane but the upper half plane
are the same in size. The plane we are using now is not an ordinary plane but the upper half plane  that is different from Fig. 6. Though it is a matter of course, one that lost its size at the origin grows again after passing. How should we understand it? It is mysterious for us even it is mathematically correct.
that is different from Fig. 6. Though it is a matter of course, one that lost its size at the origin grows again after passing. How should we understand it? It is mysterious for us even it is mathematically correct.

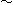
 have different a or d.
have different a or d.
 : The locus is a straight line. The arrow indicates the direction that b gets larger while b is negative. The origin is the turning point of the locus.
: The locus is a straight line. The arrow indicates the direction that b gets larger while b is negative. The origin is the turning point of the locus.
If we fix b, c and change a while keeping d = (bc + 1)/a, we get similar phenomenon as above provided that loci turn right and left.
Look at Fig. 8.
Hyperbolic segments are drawn on the upper half plane  by using Fixed-abcd method. Black spots are corresponded end points.
by using Fixed-abcd method. Black spots are corresponded end points.
///////////////////////////////////////////////////////////////////////////////

Sorry, under construction.
[Back] [Next] [Contents]
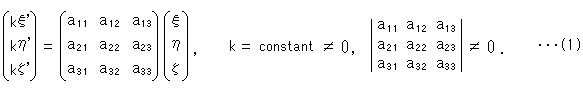
 Look at Fig. 1.
Look at Fig. 1.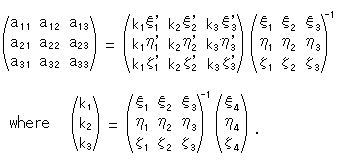
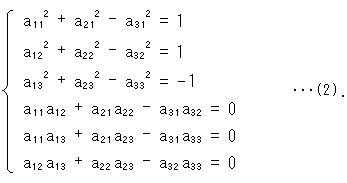
 Look at Fig. 2.
Look at Fig. 2.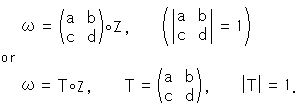
 Look at Fig. 3.
Look at Fig. 3.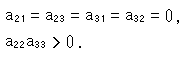
 Look at Fig. 4.
Look at Fig. 4.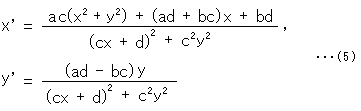
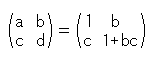
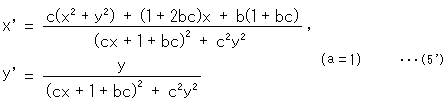
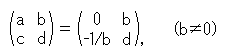
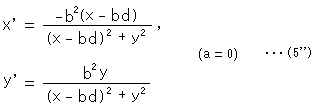
 We adopt Fixed-abcd method, and apply Mobius transformation with condition (4) to an ordinary plane. We regard the lower half plane is a mirror copy of the upper half. We do not care about the upper half plane
We adopt Fixed-abcd method, and apply Mobius transformation with condition (4) to an ordinary plane. We regard the lower half plane is a mirror copy of the upper half. We do not care about the upper half plane 
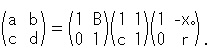
 Look at Fig. 7.
Look at Fig. 7.