ひとたび双曲的非ユークリッドの世界にはいると、その奇怪さに、あなたは立ち往生するかもしれません。 平行線が交わる話しはもちろんのこと、噂では、
｢内角の和がゼロの無限に大きい三角形がある｣、
｢ふつうの正方形は描けない｣、
｢合同はあるが相似はない｣、
｢三角形の面積は内角だけできまる｣、
｢距離と角は依存しあう｣、
などなど。
もし、双曲的非ユークリッドの世界がそんなにヘンだというのなら、具体的に見極めてみなければなりません。 手始めに、三角形と円周角を見てみましょう。
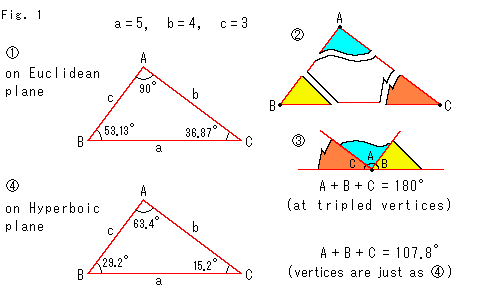
Fig.1をご覧ください。
三角形が双曲的非ユークリッドの世界ではどんなに狂っているかを見てみます。
: ユークリッド平面(Euclidean plane)上の三角形です。
: 隅を図のようにちぎります。
: そして、子供を納得させるように、3つの頂点を重ねてならべると、内角の和が正確に180
であることがわかります。
: この三角形を歪めずに双曲的非ユークリッドの世界へもっていきます。 物差しを一緒にもっていってもかまいません。 ある世界での長さというものは、その世界の性質によって定まります。 けれども、そのとき物と物差しはともに変わるのですから、aセンチの長さのものはaセンチとして測られます。 つまり、長さは変わりません。 そう考えてよいとすると、双曲的非ユークリッドの世界でもユークリッドの世界と同じ長さの辺からなる三角形が描けることになります。
いま、と同じ長さの辺をもった三角形が双曲的平面(Hyperbolic plane)上にあるとします。 その内角を測ってみると、どの内角もより小さくなっています。 その和は、聞いた話のとおり180より小です。
ところが、のようにしてみると、内角の和が180であることになります。 しかし、では3つの頂点が重ねられていることに注意しなければなりません。 つまり、頂点と頂点の間がなくなっています。 長さと角が依存し合っているために、の角A,B,Cは三角形のものと同じではありません。 のようにすれば、180という数値が出てくるのは当然です。 ですから、双曲的平面では、ちぎって動かして比べるようなことはできないのです。
実は、の内角は双曲三角法というもので計算したのです。そんな仕掛けのある平面をふつうに描くことはできません。 それで、平面はふつうの平面のままにしておいて、測り方（計算式）のほうを換えたのです。 よく「三角形の内角の和が180より小なら、そこは双曲的な世界だ」といわれます。 それは、ふつうの物差しとふつうの分度器で測ってのことです。 それが双曲三角法で計算したものと一致するのです。 実際の双曲的平面とは、そういうものです。
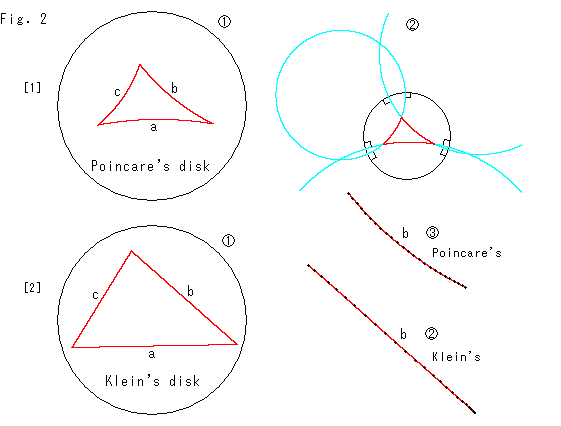
Fig.2をご覧ください。
双曲的非ユークリッドの世界の平面全体を表現したモデルとして、ポアンカレ円板(Poincare disk)とクライン円板(Klein disk)とよばれるものがあります。 それは正確な地図といってもよいものです。 円板の周は内部から見て無限遠です。 しかし、固定した経緯線のようなものはありません。 経緯線が場所によって変わるので、描き込んでおないのです。
[1]: ポアンカレ円板にFig.1のの三角形を描きました。 描く場所は円板の内部ならどこでもよいのですが、三角形の重心を円板の中心合わせています。
: 三角形の辺が円弧になっています。
: 辺が円板の周に直交する円の一部になっているのです。 そして、目で見た角と双曲平面上の実際の角とが一致しています。
: 辺の一つbを双曲的等間隔にきざんで印しをいれ、少し拡大てみたものです。 見た目に、その間隔は均一ではありません。 ちょっと見ずらいですが、端へいくほど詰まっています。
[2]: クライン円板に同じ三角形を描きました。
: こんどは、三角形の辺が真っ直ぐです。 クライン円板では、直線が直線として描かれます。
: 辺bに上と同様に印しをいれものです。
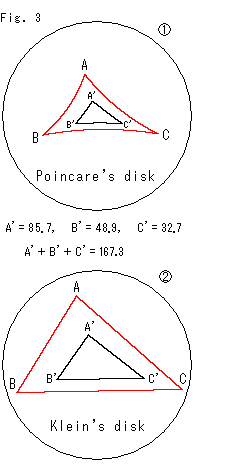
Fig.3をご覧ください。
もとの赤い三角形ABCの中に辺の長さを1/3にした小さい黒い三角形A'B'C'を重心を共有させて描きます。
: ポアンカレ円板です。 図に書かれているように、小さい三角形A'B'C'の内角が大きい三角形ABCのそれよりも大きくなっています。 それは、双曲幾何には相似はないということです。 Fig.1のと見比べてください。 三角形が小さくなるほど、内角の和は180に近づきます。
: 同様に小さい三角形をクライン円板に描いたものです。 この場合、ちょっと見た目に相似のようにも映りますが、そうではありません。 角は見たとおりでなく、辺の長さから計算されます。
ユークリッド幾何では、長さがn倍になっても、物差しも同時にn倍に伸びれば、図形が変化したことはわかりません。 ところが双曲幾何では、その変化にすぐ気付きます。 長さの変化を見出せなくても、角が違ってくるのです。 なにか絶対的な長さがあるように感じられますね。
角というものは、一周すれば元に戻るといったように40でも50でも、ちゃんとした幾何学的な意味をもっています。 ところが長さには、そのような基になるものがありません。 なにを長さの単位にしてもかまいません。 勝手に約束してよいのです。 しかし双曲幾何では、角と長さは依存しあっているのですから、長さにも絶対的な単位があると考えられます。 これについては、後でまたふれます。
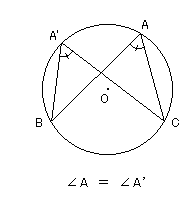
円周角について見てみましよう。
みなさんも中学校で「円周角は、あい等しい」というのを習いましたね。 それは、たしかに正しい。 ずっと昔に証明されています。 でも、なぜそうなのかは、誰も説明してくれませんでした。 「円周率は3.14だ」と小学校の先生はいいました。 でも、なぜ大きい円でも小さい円でも円周率は3.14なのでしようか？ その神秘さに、私はこわい気持ちさえしました。 それでいて、証明とか3.14になるリクツは十分納得でき、感激しました。 ですが、証明は「コト」の正しさを明らかにしただけのものであって、なぜそんな「コト」なのかを説いてはくれません。 わたしは、折りにふれ、ずっとヘンな気持ちでおりました。
ある人は「それは自然の性質だ」といい、他の人は「それはユークリッド幾何自体の属性だ」といいます。 どうも、彼らは巧く言い逃れをしているように感じてなりませんでした。
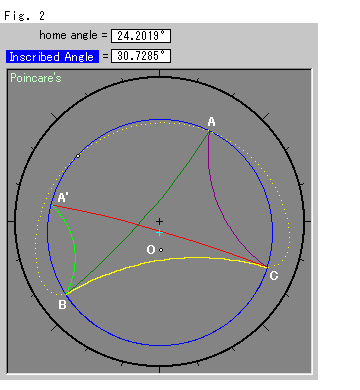
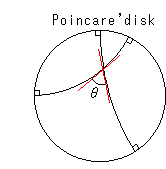
Fig.2をご覧ください。
ポアンカレ円板です。 その中では、
直線が黒い無限遠の円周に直交する円弧になります。
直線と直線の交角は、円弧と円弧の交角になります。
円は円として描かれますが、中心は外へ偏ります。
こんなことが正当でしょうか？
その吟味は、おいおいするとして、ここでは権威に（不満でも）したがってください。 なによりも、見ましょう。 モデルの正当性をいうのは、一筋縄ではいかないようだし、もっと見てから文句をいう方が、いいやすい。
円板の中心(原点)には“+”印をつけています。 中の青いループが双曲的な円で、その双曲的中心を白いスポットで示されています。 水色の“+”は、青い円の視覚的な中心です。 双曲的な円の中心Oは、視覚的な中心からずれています。 その円の上に三角形ABCをおき、黄色い辺BCを固定して、頂点Aを動かします。 いま、頂点Aを点A'のところまで動かしました。 頂点Aを円周上で動かしていくと、円周角がもとの値(home angle)から変化するのが見られます。
点線のループは、頂角Aを不変にたもちながら動かした場合の軌跡です。 辺BCから下側では、180の補角です。 その軌跡は、もはや円でも楕円でもありません。
双曲的非ユークリッドの世界では、
のです。
これだけのことなら、なにかの本を読めば、容易に察することができます。 しかし、その様子を目で見られたことがありますか。 このような視覚化が、私たちの目的の一つです。
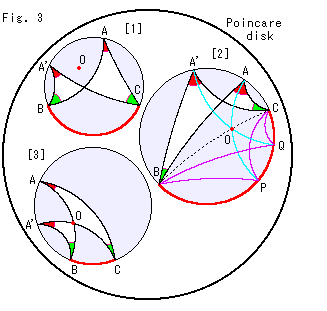
Fig.3をご覧ください。
ポアンカレ円板モデルの内部に円を描いて、円周角を見ています。 3つの円は見た目に大きさは違いますが、双曲的には合同です。 赤いスポットOはそれらの双曲的中心です。
[1]: 円周上において、赤い円弧BCにたいするの1点Aの円周角Aと同じ大きさの円周角となる点が、1つあります。 このとき、緑色の角BとB'も同じです。
[2]: 赤い円弧BCは半円です。 その両端をむすんだ直線(点線)BCは直径です。 この場合、弧BCに張った円周角Aと等しい円周角となる点がA'だけでなく、点Pと点Qにもあります。 点P,Qは、点A,A'と反対側にありますが、ユークリッド幾何のように180の補角ではありません。 水色の線のように、点Aから点Pへ、点A'から点Qへと双曲的直線を引くと、その2直線は赤いスポットの双曲的中心Oで交わる直径になります。 点AとPは直径BCに関して対称であり、点A'とQも同様です。
[3]: 赤い弧BCの一端Bから中心Oを通って弦ABを張ります。 同様に、他端Cから中心Oを通って弦A'Cを張ります。 すると、赤い弧BCに対する円周角AとA'は一致します。 つまり、円周角Aを張る直線の1つが中心Oを通るとき、その円周角と同じ大きさの円周角となる点A'から円弧BCの両端に直線を引くと、かならずその1つが中心Oを通るわけです。
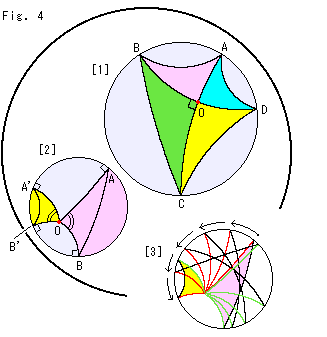
Fig.4をご覧ください。
もう少し描いてみます。 円はFig.3のと同じ大きさです。
[1]: 円の中心Oで直交する2つの直径ACと直径BDを引きます。 四辺形ABCDの内角A,B,C,Dはすべて等しくなっています。 しかし、どの内角も鋭角なので、正方形でも長方形でまありません。 双曲幾何では、けっして正方形も長方形もつくることができないのです。 内角A,B,C,Dは直径(対角線)ACかBDで正確に2等分されています。 そして、4つの半径は同じ長さですから、色分けした4つの三角形は合同です。 双曲幾何では、3つの内角が等しい三角形は、円板モデル上で見た目にどんなにちがっていても合同です。 そして、ユークリッド幾何と同様に、二等辺三角形の底角はあい等しいのです。
[2]: 円の中心Oはピンク色の扇形と黄色い扇形の共有点です。 各扇形の上に三角形が重ねられています。 扇形の辺は、すべて円に垂直です。 そして、2つの扇形は合同です。 三角形も合同です。 円周上の弧(扇形の底辺)の長さは、ユークリッド幾何と同様に半径と中心角だけできまります。
[3]: [2]のピンク色の扇形をその頂点Oを軸に回転している様子です。 回転していくと、ピンク色の扇形は黄色い扇形に三角形とともにぴったり重なります。 見た目には、小さくなっていきます。 黄色い扇形を回せば、大きく見えていき、ピンク色の扇形とか重なります。
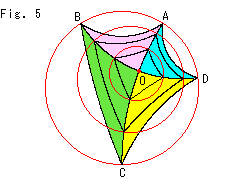
Fig.5は、Fig.4の[1]の円を小さくしていったものです。 円を小さくすると、四辺形ABCDが小さくなると同時にふつうの正方形に近づくのが見られます。 つまり、図形の角を保って大きさを変えることができないのです。 双曲的非ユークリッドの世界には、相似というものがないのです。 でも、三角形が三角形であり、四辺形が四辺形であることには変わりはありません。 どんなに大きくしようと、小さくしようと。
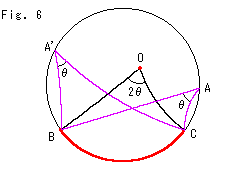
Fig.6は、ユークリッド幾何と同様に「円周角は中心角の半分」になりはしないかと、描いてみたものです。 これまでのことから、それがいえるのは特定の点AとA'だけです。 双曲幾何には同様な定理はありません。
こんな風に、円周角が変化することはわかりました。 それでは、そのような双曲的非ユークリッドの世界は空間全体としてどうなっているのでしようか。 双曲幾何とユークリッド幾何との差異を個々に追うこともときには必要ですが、私たちは空間全体の性質を先に知りたいのです。 そのために、上の円板モデルがどのようにしてつくられたのかを見ることにしましよう。