前章で、だ円的非ユークリッドの世界での直線の様子を見ました。 ここでは、三角形について見てみます。
だ円的非ユークリッドの世界で、三角形を遠くへ無限の彼方へと動かしていくと、どうなるのでしょうか。
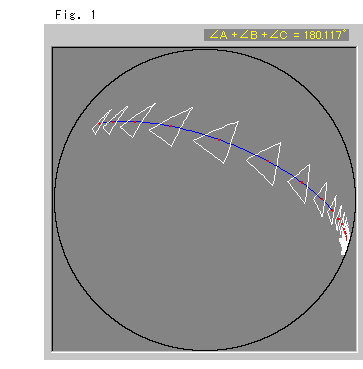
右のFig.1は、三角形を青い直線上で一定間隔に動かしてみたものです。 赤いスポットは三角形の重心です。 見た目に三角形は小さく小さくなっていきますが、実は同じ大きさです。
三角形の内角の和は、図の上の黄色い数値のように、ちゃんと計算できて、話に聞くとおり
より大です。 これは球面幾何で計算されます。
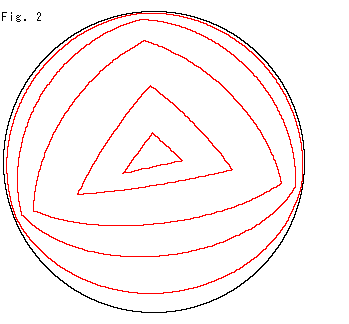
Fig.2は、三角形の大きさを変えていってみたものです。 三角形の内角の和は、より大きく、三角形が大きくなるにつれて、ますます大きくなります。 しかし、その最大値は、3です。 このとき、三角形は円板の縁(円周)になります。
ユークリッド半径１の球面では、内角がA,B,Cの三角形の面積Sは、
となります。 面積Sの最大値は、2です。 それは、半球面の面積そのものです。そして
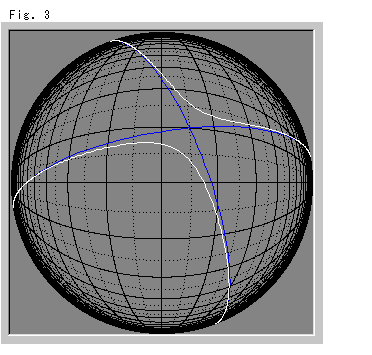
Fig.3は、ついでに前章にならって双曲線を描いてみたものです。 奇妙な格好ですね。 青い曲線は、漸近線です。 ひょっとしたら、白い双曲線は、球のように見える円板の裏側でつながっているのかも知れません。
正しいとされている楕円幾何のモデルの条件は
モデルの形は球面である（半径1）。
大円を直線とみなす。
長さは、球面上のユークリッド的長さである。
直線の長さは有限で、その最大値は
となる。
角は、大円と大円のユークリッド的交角である。
対心点を同一視する。
というものです。
これまでに描いた図は、この条件を満たしていません。 まず、この条件には無限遠が含まれていません。 それに、モデルの形は球全体です。 どうも不都合な気がしますね。
ともかく、「双曲的非ユークリッドの世界」へ進みましよう。 そして、双曲幾何と対比するときに、モデルの工夫をすることにします。