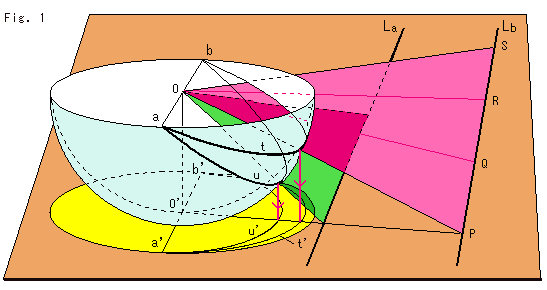
Fig.1をご覧ください。 これは、ユークリッドの世界をだ円的非ユークリッドのモデルに写すツールです。 水色の半球面が、私たちのモデルです。 黄色い円板も私たちのモデルです。 どうしてこんなところへ来たのかを話す前に、まず、このツールのはたらきを見ましょう。
いま、机の上(ユークリッド界)に平行線La,Lbがあります。 直線Lb上のP,Q,R,S,,,などのすべての点が半球の中心Oに向けて射影され、図の赤い平面をつくり、半球面上の大円tを形成します。 同様に、直線Laは半球面上の大円uを形成します。 La,Lb上の無限の彼方は、有限な直径の端a,bにとり込まれます。 下向きの赤い矢印のように大円t,uを円板モデルに正射影すると、だ円t',u'が得られます。 だ円t',u'は円板の端a',b'に端点をもちます。 これらのt,uやt',u'を直線とみなすことにします。
リーマンは、だ円的非ユークリッドの世界の直線は球面上の大円だといっています。 しかし、そのままでは、2直線が2点で交わるということになって、直線としての資格を失います。 そこで彼は、点aと点bを同一視しました。 ちょっと、ずるいですね。 でも、この手のテクニックはよく使われるのです。
リーマンは、対心点(中心に関して対称な点)をすべて同一視した球面をとって、その上で成り立つ幾何を考えました。 それが、だ円幾何です。 ですから、私たちのモデルはだ円幾何のモデルではありません。 けれども、無限の彼方を私たちの視界に取り込むということでは、私たちのモデルも十分役立ちます。 しかもリーマンの円幾何のモデルは球面ですが、私たちの円板モデルは平坦なので見やすい。
大円を直線だとしたのですから、だ円幾何には、交わらない直線としての平行線はありません。ですから、Fig.1の仕掛けをだ円的非ユークリッドの世界とユークリッドの世界を行き交うツールとするには、その都度、長さの測り方も直線や平行線の解釈(定義)も変えなければなりません。
t,uやt',u'を平行線だとし、点a,bや点a',b'を無限の彼方だと想えば、ユークリッドの世界全体をふつうの紙の上に描けたことになります。
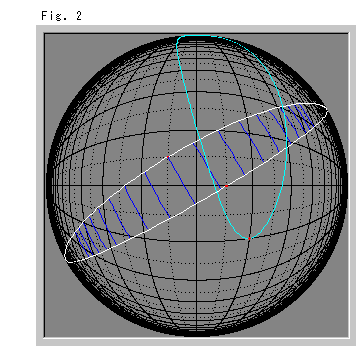
さて、Fig.1の黄色い円板の色を変えて、みなさんの方へ向けてみますと、Fig.2の黒い円板のようになります。 また、水色の半球面を下から見ているのだとしてもよいものです。 黒い曲がった格子線は、その感じを出すために、半球面の縦横を軸とする大円を描きいれたものです。
これは、楕円的非ユークリッドの世界で、その縁は無限遠です。 無限遠では、軸方向というものがないように見えます。 2本の白い曲線は、大円の黒い格子線をふつうの直交座標のように見立てた平行線です。 その平行線にまたがっている青いはしごのような線は、観察の便のために等間隔に並べたものです。 水色の曲線は、同様に描いた放物線です。
このFig.2を見ると、私たちのだ円的非ユークリッドの世界のモデルでは、平行線(白)が無限遠点でたがいに出会っています。 それは、ループをなしているようです。 水色の放物線を見ますと、これもループに見えていますね。 平行線と放物線は、無限の彼方でどこかが同じなのでしょうか?
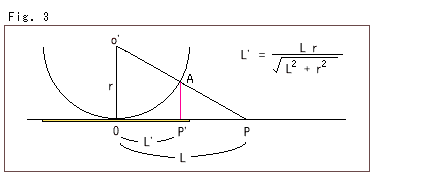
実は、私たちは,非ユークリッド幾何なんって思ってもいませんでした。 ただ無限大までも描こうとしていたら,こんなものが出てきたのです。 描くには、無限を有限に閉じ込めねばなりません。 そこで、Fig.3のように計算をしました。 その後、手元の本を開いて、だ円的非ユークリッドのところを見ると、なんだか似たような式が並んでいるではありませんか。
それじゃあ、双曲的非ユークリッドの世界って、どんなのだろうか? と、手探りをはじめたのが、このHページです。
無限遠を有限に閉じ込めるだけなら、Fig.3の半球面や式を使う必要はありません。 例えば、円錐を使ってもよいし、 y = Arctan x といったものでもかまいません。