双曲的非ユークリッドの世界のモデルには、ポアンカレの円板、クラインの円板、半球モデル、上半平面、双曲面モデル、二元グラフ、ベルトラミーの擬球などという、いくつもあります。 しかし、円板モデルだけが、双曲的非ユークリッドの世界（平面）を一望できるものです。 ここでは、ポアンカレとクラインの2つの円板モデルと、それらに関連して双曲面モデルを見ておきます。
円板モデルの半径は、曲率とか計量というものに依存しますが、簡便のためにユークリッド長で１にとります。
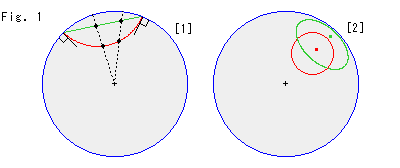
Fig.1をご覧ください。
ポアンカレとクラインの円板を重ねて描いています。 ポアンカレの円板では、直線は円板の周（無限遠の円周）と直交する円弧(赤色)で描かれますが、クラインの円板では、直線は、やはり直線(緑色)になります。
[1]: 同じ双曲直線をポアンカレ円板とクライン円板に描いたものです。 赤と緑の対応する直線上の点は、点線で示すように円板の中心から出ている直線に乗っています。
[2]: 原点から同じ双曲距離1.5のところに中心をとった双曲半径1の双曲円です。 双曲円は、ポアンカレ円板では円(赤)として描かれますが、クライン円板では、だ円(緑)になります。 いずれも中心がずれて見えます。
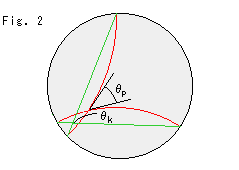
Fig.2をご覧ください。
角
と
は、双曲的角として同じです。 しかし、ポアンカレの円板では、は見えている通りですが、クラインの円板では、は、図のように赤いポアンカレの曲線に描きな直してみるか、計算しなければなりません。
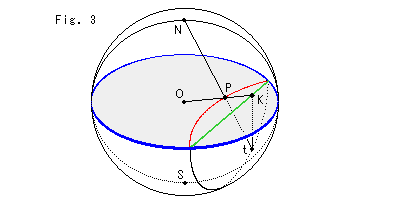
Fig.3は、ポアンカレの円板とクラインの円板の関係です。 点Oは、球と青い縁のモデル円板の共通の中心です。 この円板は、クラインとポアンカレのモデルに共用します。 点Pはポアンカレ円板上の点で、点Kはクライン円板上の点です。 両者は対応しています。 点Nと点Sは、円板を赤道面とした北極と南極です。 点tは南半球面上にあって、直線Ktは垂直です。 つまり、点N,O,P,K,tは同一平面上にあります。
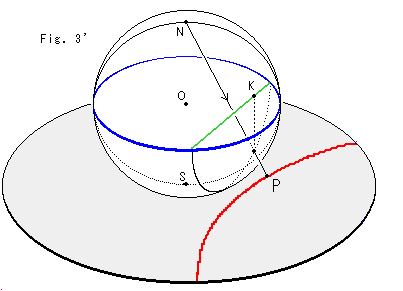
Fig.3'は、ポアンカレの円板を得るのにクラインの円板からFig.3のように上がったり下りたりせずに、直線を円弧に直接換えるものです。 ただし、できた円板は直径が2倍になっているので、そのように見なければなりません。
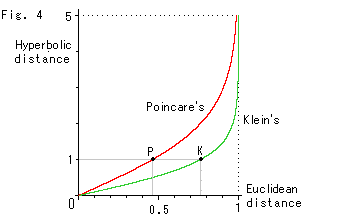
原点からの距離をポアンカレの円板とクラインの円板でくらべると、Fig.4のようになっています。 この図の点P,KがFig.3の点P,Kに対応しています。 双曲距離(hyperbolic distance)が0.5くらいのとろまでは、2つの円板上の目で見た距離(ユークリッド距離, Euclidean distance)は、およそ 1:2 になっています。
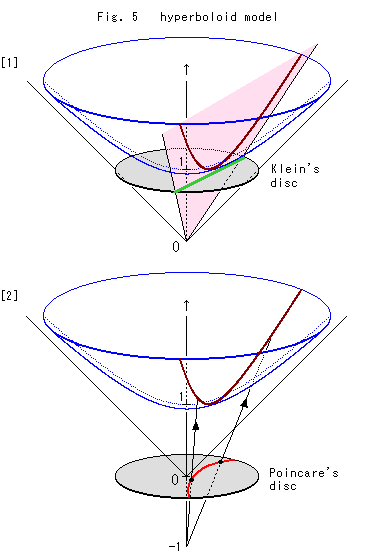
Fig.5は、双曲面モデル(hyperbolid model)です。 これは、直角双曲線の回転面です。 ふつう双曲回転面といわずに、たんに双曲面とよばれています。 双曲面モデルのことをミンコフスキーモデルとよぶ人もいます。
双曲面の底が原点Oから1のところになっています。 モデルとしては、上の方へ無限に延びているのですが、見やすくするために途中で切っています。
[1]のように、双曲面の上での双曲直線は、原点Oを通る平面(ピンク)との交線(茶色)になっています。
双曲面の底に円板をおいて、ピンクの平面と交わるところをとると、クライン円板上に対応する緑色の直線が得られます。
[2]のように円板を原点Oにおいて、回転面の軸の-1のところから、円板を貫通して双曲面上の茶色の双曲直線をなぞると、ポアンカレ円板上に対応する赤色の直線(円弧)が得られます。
双曲面をモデルとよびましたが、いうまでもなく、双曲面がそのままモデルになっているわけではありません。 モデルとしての約束事、距離の定義(計量)を入れて、はじめてモデルになるのです。 ところが、最短距離(測地線)を直線とみる約束だけで、回転面そのままがモデルになっているものがあります。 あとの方で触れるベルトラミーの擬球というのがそれです。
[注]
今後、モデル上で見た目にどんなに映ろうとも、
直線，円，平行，平行線，平行移動，
長さ，間隔，面積，
角，直角，直交，垂線
などというときは、とくに断らないかぎり、双曲的非ユークリッドの世界におけるものを指すものとします。
あるモデルから他のモデルをつくり出す方法は他にもいくつかあります。 しかし、それはあとにして、先にいろいろと見ていきましよう。