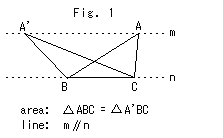
左のFig.1は、小学校で習った三角形の等積変形です。 これが成り立つのは、ユークリッド幾何でのことですね。 双曲的非ユークリッドの世界ではどうでしょうか。
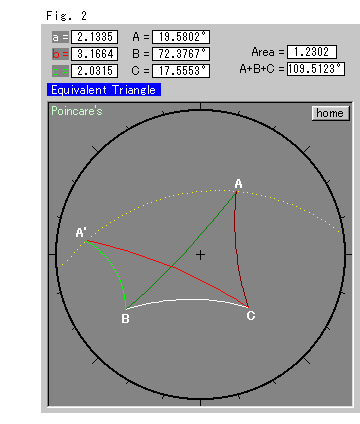
Fig.2をご覧ください。 三角形ABCの辺BCを固定して、面積Sを変えずに、頂点Aを動かします。 等積変形です。 頂点Aを動かしていくと、図の上部に表示されている双曲的面積(Area)の数値は一定ですが、他の数値は頂点Aの動きにつれて刻々変化していくのが見られます。 そして、動いた頂点Aの軌跡は黄色い点線のようになります。 図は、点A'まで動かしたところです。
この軌跡は、固定辺BCを延長した直線に関して、平行でもなく等距離でもありません。 直線でもありません。
双曲的非ユークリッドの世界では、三角形ABCの面積Sは、
- (A + B + C) 
(1)
だという奇怪なことになっているためです。
なんって。 すぐには、信じられません。
式(1)は、どこから出てきたのでしょうか。 等積変形で三角形ABCが三角形A'B'C'になったときは、
が保たれます。
球面幾何では、半径rの球面上の三角形の面積Sは、
((A + B + C) - ) (2)
です。
ランバートは、双曲幾何は虚球面幾何に相当すると指摘しました。 もっとも、彼自身は双曲幾何を信じませんでしたけれど。 いま、半径rを
(= 
)で置き換えると、上の式(1)を得ます。 虚数半径の球面なんて、とても想像しにくいですね。 でも、後の方でそれにもふれていくことになります。
Fig.3をご覧ください。
双曲幾何のモデルをすこし見たので、楕円幾何のモデルと対比してみます。 楕円幾何のモデルは球面なので双曲幾何の平坦な円板モデルと比べるには不便です。 それで、ちょっと工夫してみました。
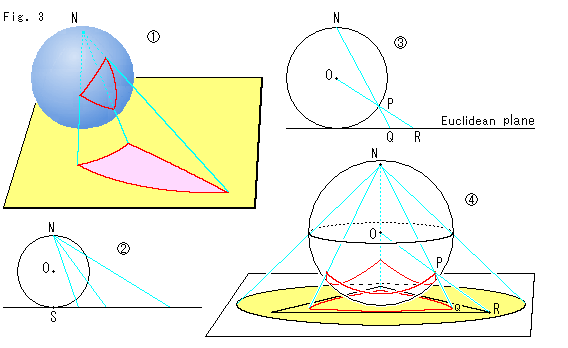
: 黄色い平面上に置いた青い球面は楕円幾何のモデルです。 その北極Nから出る射線で球面上の三角形を平面に移しています。
: 平面を水平にし、透かして眺めたものです。
: 球面上の点Pを北極Nから射影してユークリッド平面(Euclidean plane)上の点Qへ移し、同じ点Pを球面の中心Oから射影して平面上の点Rへ移したところです。
このような北極Nから出ている射影を極射影よび、球面をリーマン球とよばれています。 球の中心Oから出ている射影には既存の呼び名がないので、球心射影と名づけておきます。
: 球面正三角形を球面の真下に置いたときの極射影の様子です。 赤道面も同時に射影しています。 この極射影された赤道面を私たちの楕円幾何の円板モデルとします。 ただし、南半球面だけに注目してのことです。 というのは、楕円幾何のモデルとしてのリーマン球の対心点は同一視されるので、北半球は無用だからです。 私たちの円板モデルとしては、赤道上の対心点も考えないことにします。 そうしないと、円板が射影幾何のものになってしまうからです。 つまり、双曲幾何の円板モデルと同様に開円板ということにします。
ユークリッド平面との関係では、極射影よりも球心射影のほうが適切であることがCh.3から肯けます。 そこで、ユークリッド平面上の点Rをいったん球心射影して球面上の点Pにし、その点Pをあらためて極射影でもとの平面（楕円幾何のモデルになる平面）へ移して点Qとします。 つまり、球面はユークリッド平面から私たちの楕円幾何の円板モデルへ移るときの中継地です。 極射影を用いるのは、それだと等角ですのでポアンカレ円板モデルと見比べるのに都合がよいからです。
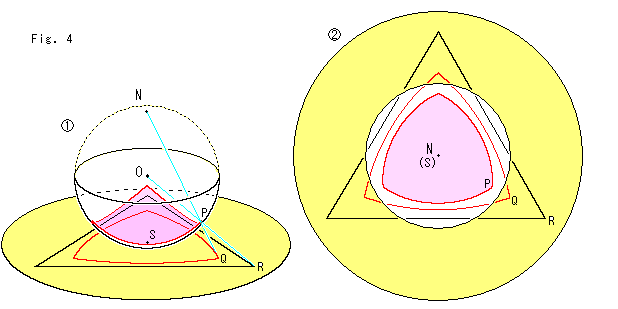
Fig.4をご覧ください。
: 上のFig.3のをこちら側へもう少し傾けて、平面上の様子がよくわかるようにしました。 球面を南半球面だけにして、平面のフレームは省いています。 球面三角形をピンクに染めています。 球心射影 O-P-R は平面上の黒い三角形を平面上に形成し、極射影 N-P-Q は赤い三角形を平面上に形成しています。
: 全体を真上から見たところです。 赤い三角形はピンクの三角形と等角ですが、黒い三角形はそうではありません。 赤い三角形の辺は曲がっていますが、黒い三角形の辺は直線状になっています。
こうすることで、ユークリッド平面とリーマン球面と私たちの楕円幾何の円板モデルの三者間を移りあえるというわけです。 極射影はいわゆる等角写像ですから、球面上の角と平面上に射影された角は、つねに一致します。 球心射影では角は保たれませんが、球面上の直線(大円)は平面上の直線になります。 ということは、ユークリッド平面上の2直線は球心射影で2つの大円になり、その2つの大円は極射影で大円と大円のなす角を保って私たちの楕円幾何の円板モデルに移されることになるのです。
円板の半径はもとの赤道半径の2倍ですが、ポアンカレ円板モデル(半径=1)と同じ大きさに描くことにします。 正三角形を選んだのは、たんに作図の便のためです。 むろん、私たちの楕円幾何の円板モデル上でも、長さの測り方（計量）は球面上のそれとは違います。
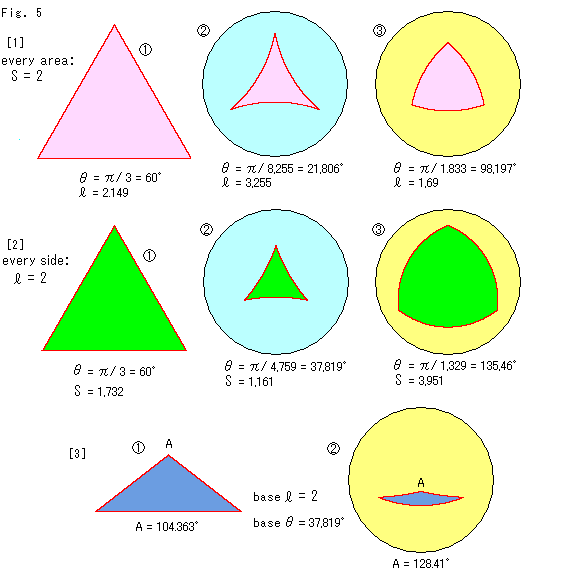
Fig.5をご覧ください。
[1]: 正三角形の面積Sを2にとります。
: 正三角形をユークリッド幾何で描いています。
: 同じ面積Sの双曲正三角形をポアンカレ円板上に描いたものです。
: 私たちの楕円幾何の円板モデルに面積Sの楕円正三角形を描いたものです。
面積の計算は、上の式(1),(2)に拠っています。 
は三角形の内角です。 正三角形にしてあるので A+B+C = 3 です。 どの図の内角も目で見た通りになっています。 つまり、面積が同じでもそれぞれの三角形の内角は違うのす。 
は辺の長さです。 楕円幾何での辺の長さは、球面の大円の対応部分のユークリッド的長さです。 ユークリッド三角形が特に大きく見えますが、どの三角形もそれぞれの幾何で同じ面積2です。
[2]: こんどは正三角形の辺の長さを2にとっています。 すると、,,のようになります。 大きさはずいぶん違って見えますが、辺の長さはすべて同じです。
[3]: 二等辺三角形です。 参考のために、ユークリッド幾何での合同条件である二角夾辺の三角形を比べてみます。 底辺(base)の長さを[2]のと同じ2として、その両端の内角を同様に37.819
にとっています。 はユークリッド三角形で、は私たちの楕円幾何の円板モデル上の三角形です。 上側の頂点の内角は図に示されているように、3つの三角形で異なっています。
ところで、"同じもの"ということを広く考えてみましよう。 面積が変わらない[1]で、そのことだけに注目すると、3つの三角形は同じものといえます。 辺の長さが変わらない[2]でも、そのことだけに注目すれば、やはり3つの三角形は同じです。 しかし、それらを合同というわけにはいきません。
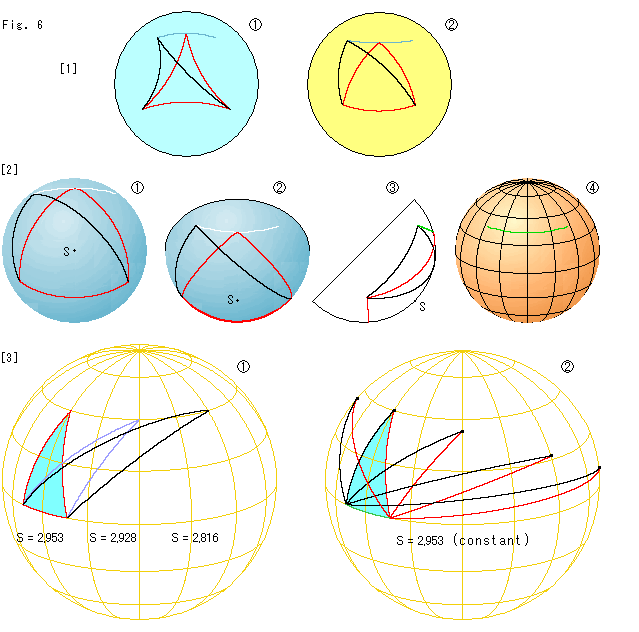
Fig.6をご覧ください。
さて、三角形の底辺を固定してFig.2と同様に等積変形をしてみます。
[1]: ポアンカレ円板と私たちの楕円幾何の円板モデルを並べています。
: 緑色の曲線は、黒い三角形のように等積変形していったときの頂点の軌跡です。 それは
形に曲がっています。
: 三角形の面積はポアンカレ円板のと同じです。 こんどは、頂点の軌跡が逆に
形になっいます。
こうして並べてみると、双曲幾何の平面が楕円幾何の平面と逆の性質をもったものであることがよく察しられます。
でも、このを見ただけでは、頂点の軌跡がどんな曲線なのかよくわかりませんね。
[2]: それを知るために、私たちの楕円幾何の円板モデルの射影元である半球面での等積変形の様子を見てみます。
: 半球面を真下の南極S側から見たところです。 動かした頂点の軌跡を白い曲線で描いています。 軌跡が形に見えるのは、球面だからです。 半球面上の三角形が円板上のと比べて殊に大きくなっているのは、円板の大きさを双曲円板と揃えてあるからです。 この半球面上の三角形は円板上のそれとよく似ていますが、むろん相似ではありません。
: 半球面の南極Sを下の方へずらせて見たところです。 当然ですが、頂点の軌跡が形に見えます。 球面上でやのように見えても、円板へ移したときは[1]ののようになるのです。
: を左から透かして見ると、こうなっています。
: 経緯線をいれた別の球面に軌跡だけをとって描いてみたものです。 この経緯線の南北(地軸)の傾きは、緯線と軌跡を見比べやすいように適当にとっています。 ,と同じではありません。 これで見ると、軌跡は緯線になっていているのかも知れませんね。
[3]: それを確かめてみましよう。
赤道上にのように底辺を固定して、上側の頂点を緯線に沿って動かしてみました。 すると、わずかですが面積Sが変化しています。
そこで、面積Sを一定(constant)に保ちながら上側の頂点を動かしてみると、のように、軌跡は描くまでもなく、緯線とはまったく違ったものになります。 のこちら側の半球部分だけをとって、そこに三角形を描いています。 私たちの円板モデルに極射影できるのは、半球面だからです。
球面だとして向こう側へ頂点を動かしていくこともできますが、基準にとった水色の三角形の経度と反対側では3頂点が赤道上になってしまって、三角形をつくれません。
やはり双曲幾何のFig.2と同様に、軌跡は三角形の底辺(大円)に関して楕円的な平行ではありません。 もともと楕円幾何には平行線はないのですから、当然です。 緯線のような等距離線でもありませんし、直線(大円)でもでもありません。 球面を適当な平面で切ってできる小円にもなりません。
等積変形での楕円幾何との対比から双曲幾何のイメージアップをこころみてきましたが、双曲幾何にもリーマン球のような都合のよいものが欲しいですね。 似たような考え方があるに違いありません。 おいおい見ていきましよう。