双曲的非ユークリッドの世界のいくつかの絵をみてきました。 ここでは、その根源であるところを見ていきます。
Fig.1をご覧ください。
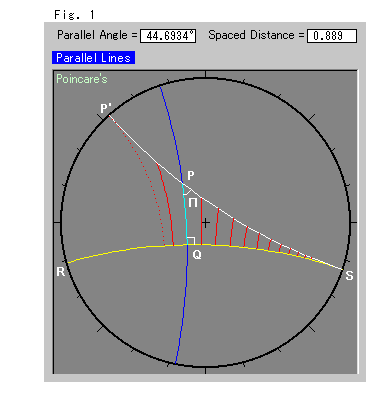
直線RSとその直線外の1点Pが与えられて、点Pを通る直線P'Sが描かれています。 双曲的非ユークリッドの世界では、直線P'Sは直線RSに平行です。 平行線は、平行方向(点Sの方)へ向かって遠くへ行くほど、たがいに近づいていきます。 2本の直線は、無限遠(円板の縁)で共有点Sをもっているように見えます。 赤い線と青い線は視覚の便のためのもので、直線RSに直交して双曲的等間隔に並べられています。 赤い点線はP'へ向かっているものです。
角SPQが、ロバチェフスキーの名付けた
平行角
と呼ばれているもので、一般に
（パイ）と表されています。
点Pを通る平行線をもう１本、PRと引けます。 つまり、与えられた直線RSに関して、1点Pを通る平行線が２本あるわけです。 ミステリーですね。 いや、そうではありません。 ともかく、双曲的非ユークリッドの世界に留まってください。
Fig.2をご覧ください。
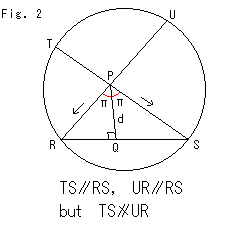
直線が直線として見れるクラインの円板です。 直線RSに平行な直線が、直線RS上にない一つの点Pを通って、TSとURの2本あります。 矢印がそれぞれの平行方向です。 ユークリッド幾何では、1本の直線に平行な直線は、すべて平行です。 直線RSに対して直線TSも直線URも平行ですが、直線TSとURは平行ではありません。 無限遠である円板の周上で、それらが共有点をもっていないからです。
ロバチェフスキーが発見した平行角の公式は
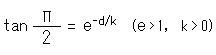
です。 簡単のために、eは自然対数の底とし、kは1としておきます。 (これらについては、あとで議論します｡)
平行角は
/2より小ですから、右辺 
は1より小です。 dは平行線間の双曲的距離PQです。
さて、平行角の公式をよく見ると、角が距離dの関数になっているではありませんか！ 先ずもって、つぎのルールを受け入れねばなりません。
同意なさいますか？
角と距離は、まったく異質のものですね。 それをイコール“＝”で結びつけるとは、―――。 先駆者のいく人かは、平行角の公式に近づいていながら、これを在り得ないことだとして放棄してしまいました。 しかし、ロバチェフスキーらは、万有引力が距離と依存しあうのと似て、何ら不思議なことではないのだと考えたのです。
平行角の公式はロバチェフスキーとJ.ボリヤイとガウスによって、それぞれ独立に1826年頃に発見されました。
それが、「平行線は交わるんだ」という仮定から、どのように導き出されのかという事については、とても興味をおぼえますね。 しかし、ここではそれを詮索するよりも、彼らが構築した、ユークリッド幾何にはない、距離と角の関係に注目しましよう。
(ロバチェフスキーらのしたことをどうしても辿りたい方は、寺坂秀孝の「19世紀の数学 幾何T,U」共立出版 などを見るとよいでしょう｡)
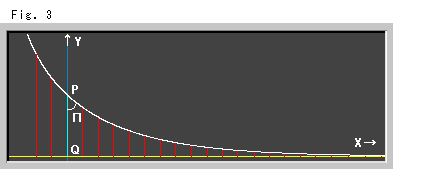
Fig.3の曲線をご覧ください。
これは、ふつうの平面の上で、X軸とY軸の方向だけに注目して、双曲的平行線を描いたものです。 黄色い基準直線RSをX軸に置き、双曲的平行線間の双曲的距離をそのままY軸方向にとっています。 赤い線分は双曲的長さで等間隔に立てたものです。 その長さをふつうの物差しで測れば、双曲的平行線間の距離が得られます。 指数曲線のように見えますが、そうではありません。 曲線上にふつうの分度器をあてれば、曲線上の各点での平行角が読み取れます。
それにしても平行線は、無限遠で本当に共有点をもつのでしょうか？ Fig.3の右の方を見れば、うなずける気もするのですが、みなさんは、いかがですか。
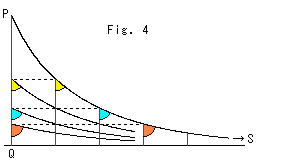
Fig.4をご覧ください。 Fig.3と同様に描いたものです。 平行線PSに沿って共有点Sの方へ行くと、平行角がしだいに大きくなり、/2に近づいていきます。 同じ色のところの平行角は同じです。 これは、平行角だけに注目したとき、点Pから右の無限遠の方へ行くのと点Qへ降りて行くのが、同じ状況にあることを示しています。 無限へ行くのとゼロへいくのが同じ！