ロバチェフスキーは、平行線とは無限の彼方で交わるものだと仮定しました。 どのように考えたのでしようか。 私たちなりに理解してみましよう。
ユークリッドの原論から平行線に直接関連して注目されるものを挙げますと：
定義23
平行線とは、同じ平面上の2直線であって、両方向にいくら伸しても、
そのどちらの側においても交わらないものである。
公準1
2点をむすぶ直線は、1本あって、1本に限る。
公準2
直線は、いくらでも伸ばすことができる。
公準5
1直線が他の2直線を切っている。その2直線を十分伸ばす。
すると、
その2直線は、内角の和が2直角より小さい側で交わる。
ユークリッドのいう“直線”は有限な線分のことです。 本によって、いろいろな表現で訳されていますが、意味に差異はありません。 Webにも沢山あります。 (英文では、Euclid's Elementsなど)
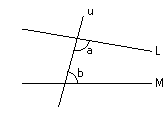
私たちの公準5の理解は
右図において、u,L,Mは有限な直線(線分)です。 もし a + b < 
ならば、LとMは、十分に伸ばした
とき、a,bの側で交わる。
というものです。
ユークリッドは、特定の場合 a = b = /2 や a + b = については、交わるとも交わらないとも言っていません。“いくらでも”とか“十分に”とはいっていますが、“無限に”とはいっていません。 なんと巧妙に、彼は無限を避けているではありませんか！
双曲的非ユークリッドの世界の公理(あるいは定義)は
です。
ロバチェフスキーは、しかし、直線についても無限についても、何も言っていません。 矛盾がないことの証明もしていません（ユークリッドとて、そうですけれど）。
さて、ロバチェフスキーのキーポイントを見てみましょう。
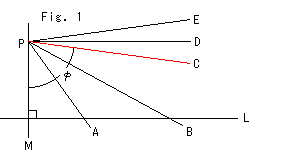
Fig.1をご覧ください。
直線Lを引き、その上にない点Pをとります。 直線PMは直線Lに垂直です。 点Pから放射状に直線A, B, C,,,をひきます。 赤い直線Cから下の直線A, Bなどは、直線Lを切ります。 赤い直線Cから上の直線D, Eなどは、いくら延長しても垂線PMから右側で直線Lと交わりません。
赤い直線Cは特別で、直線Lと交わるのか交わらないのかわかりません。 そんな直線Cが存在するとして、直線Cは直線Lに関して平行であるといいます。 そして、角
が、あの平行角
です。
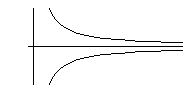
ずっと昔の5世紀にプロクルスが、こんな不審をいだきました。
彼は、「1本の直線が他の2本の直線に直角に交わっているとき、その直角を鋭角に変えると、2本の直線はたがいに傾きあう。 この傾きあった2本の直線は、伸ばしていくと、かならず交わるだろうか？
ある傾きあった2本の曲線は、いくら伸ばしても交わらないという事実がある。（漸近線を挟んで向かいあっている双曲線のようなものを思ってのことでしよう｡） だから、2本の直線はずっと傾きあっていても、交わらないことがあるのではないか｡」といぶかったのです。 右図の2曲線は、確かにどこをとっても、どこまで辿っていっても、傾きあっています。 それでいて、けっして交わりません。 なんとプロクルスは、鋭いではありませんか！
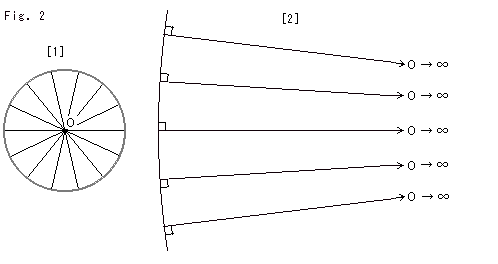
Fig.2をご覧ください。
ロバチェフスキーに戻りましよう。
[1]: 円Oの円周上の1点を固定します。 そして、中心Oを無限の彼方へと蹴り飛ばします。
[2]: すると、円周は伸びて直線になろうとし、半径は無限に大きくなります。
ロバチェフスキーは、この円を極限円と名付けました。 彼は、[1]が可能で、その結果が[2]だと仮定したのです。
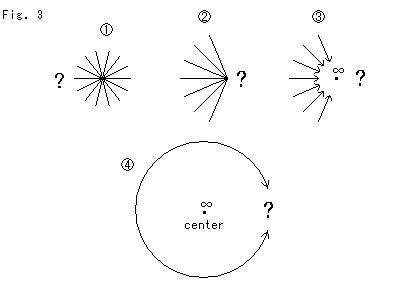
Fig.3をご覧ください。
ここに素朴な問答を挿入させてください。
: 円の中心付近は無限遠で、このようになっているのですか?
そうではありません。 なぜって、中心が無限遠なら、それを越えた向う側というものは無いのですから。
: それじゃあ、こんな具合ですか？
いいえ、違います。 まず、私たちは、無限遠には場所というものがないことを認識しなければなりません。 もし無限遠という場所があれば、その向こうを考えることができるので、実際にはそこは無限遠ではないのです。「無限遠はあの"方向"に在る」と想うのは自由ですけれども、
無限の彼方という "ところ" を想ってはならない
のです。 想うことすら許されないのです。 想えば、その先を指すことができてしまうからです。
: そうすると、これでいかがですか。
ダメですよ。 いま言ったことに反してはなりません。 矢線が有限のところにあるとしても、ダメです。 なぜなら、すべての半径が中心の周りに対称的に等しくなければならないからです。 もし、図が無限遠の近くを表現するものなら、それはまったくナンセンスです。 無限遠からの遠近というものはありません。
でも、「無限遠点の近傍というものが考えられる」と聞いたことがありますよ。 それをはっきりさせればよいのではありませんか？
そうです。 だけど、双曲幾何においてそれを明らかにした人はまだ世界中にいません。
: 結局、なにもわからないということですね。 円は閉じたループであるのに、中心が無限遠だというのなら、その無限遠を越えたところが存在しなければ、円が円ではなくなるではありませんか？
いや、むづかしいですね。 ロバチェフスキーは、「円の中心を限りなく無限遠へと追いやれば、その極限において」といったはずです。 "限りなく" とか "極限" ということばは
論法で厳密に定義されているようですが、私たちにとって直感的には、やはり曖昧ですね。 限りなく無限遠へと進んでも、けっして無限遠に達することはできません。 無限遠とはそういうところですから。 したがって、Fig.2の[2]は円の中心が無限遠へと向かって進んでいる進行中の図です。 その進行には終着点がありません。 ロバチェフスキーは、そういう進行中の極限を考えたのです。 つまり、極限円はいつまでも円です。 その半径と直径は、
のです。 際限もなく大きな有限の値です。 なぜか、そんな値の記号も用語もありません。 発明しておきましよう。 記号で 
と書いて無量値とよんでおくことにします。 無量値は際限もなく大きいのだけれども、その隣に無限大があるのではありません。 もし無量値とした値より大きい値があれば、その大きい方を無量値とすればよいからです。 有限の限りは無限ではないのです。
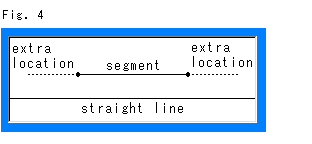
Fig.4をご覧ください。
線分(segment)には端があります。 閉じてないものでも、境界としての端があります。 そして、線分は好きなだけ、いくらでも伸ばすことがきます(ユークリッド公理)。 しかし、無限遠にまで伸すことはできません。 なぜなら、線分では図のように、つねに両端に延ばすことができる余分な場所(extra location)を占めることができるからです。 ふつうに直線(straight line)というとき、無限に長いものを指します。 直線には端がまったくありません。 ですから、直線は、線分を伸ばしたものではないのです。
ロバチェフスキーにもどって、耳を傾けましょう。 以下は、わたくたちの理解です。 彼のいったままではありません｡
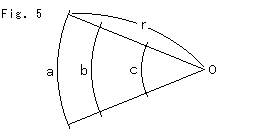
Fig.5をご覧ください。
円弧a,b,cは同心円の部分で、ユークリッド幾何での長さを表しています。
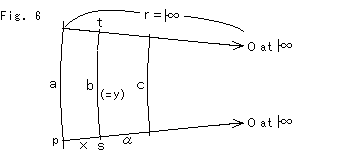
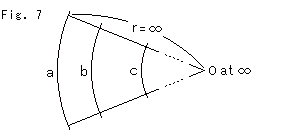
Fig.6のように中心Oを無限の彼方へ追いやります。 無限の彼方へとうのは、無限の彼方へ向けてということで無限の彼方までではありません。 図に記号で示してある通りです。 円周は中心Oの向こう側を通って、ちゃんと一周しています。 半径rは無量値ですので、その2倍の無量値をとることもできるのです。 a,b,cは直線とみなせるものですが、同じ長さではありません。
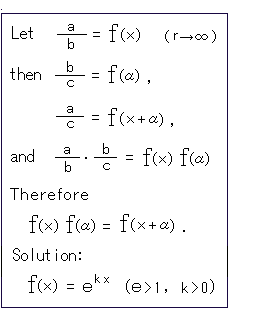
左の囲みを見てください。
簡単のために、 a = 1 k = 1 e = 自然対数の底 にとります。
b,cは、a = 1 に応じた値になります。 kは長さの単位に拠る定数です。
さて、bを変数yに書き換えると、 a/b = f(x) から
1/y = f(x)
そして、
y = exp(-x) --- (*)
ここに
x = 距離 ps,
y = 距離 st.
を得ます。
この式(*)が、革命的な ロバチェフスキーの出発点です。
これを見ると、 x = 
としても差し支えありません。 それなら無量値なんて持ち込まずにFig.7のように考えて、無限遠にある中心Oの周辺のことを忘れておくことにしてもよいですね。 実際、双曲幾何には無限大そのものは含まれていません。 ですから、Fig.3の問答にかかわる必要はないということになります。 ロバチェフスキーらもこのように考えて、公理としたのだ推測されます。 つまり、平行線は交わるとしたのです。
その公理はあくまで仮定であって、ユークリッドの公理よりこちらの方が正しいといっているのではありません。 よくいわれているように、どちらの公理を採るかはまったく自由です。
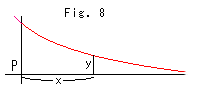
Fig.8は式(*)のグラフです。 曲がっていますね。 お馴染みの指数曲線です。 直線がこのようになるというのではありません。 上のFig.7では真っ直ぐに描かれていますが、いまそれは思考図だといえます。
ロバチェフスキーは、式(*)から半径無限大の球(極限球)を巧みに使って、あの平行角を発見したのです。 そして、双曲三角法を導き出しました。 その双曲三角法を使った幾何が双曲幾何です。
これで双曲幾何は出来上がっているわけですが、そのままでは具体的に目に見えるものがありません。 高次元の話とか電子などのことなら、はじめから抽象的であって、それなりにイメージできます。 しかし双曲幾何では、双曲平面そのものではありませんが、上にあるような図が描けます。 幾何学は目に見えるものを対象としてきました。 そのため、一見は百聞にしかず（見ないと信じられない）といったこともあって、人々はこの抽象世界をそのまま受け入れようとはしませんでした。 それを救ってくれたのが、モデルです。
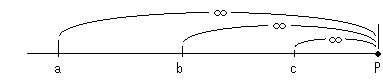
そうです。 モデルを使えば、無限大を描くことができます！ 「モデルを使えば」というのは、右図のようにa,b,cのどの点から点Pを測っても無限大の距離になるように距離の測り方を約束しておくことです。 上で「無限の彼方という "ところ" を想ってはならない。 想えば、その先を指すことができてしまう。」といいましたが、それは正確ではありません。 距離の測り方をちゃんと定めておけば、"その先" は存在しません。 ですから、
無限の彼方は、想うことも描くこともできる
のです。
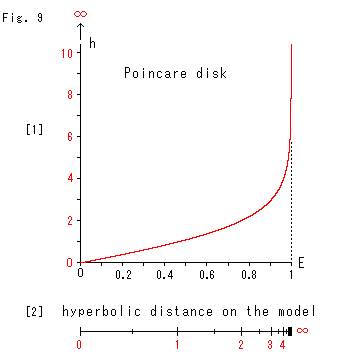
Fig.9をご覧ください。
ポアンカレ円板の原点からのユークリッド距離Eと双曲距離hの関係を見てみましよう。
[1]: 測り方（計量）によって異なる長さの対比です。（縦軸のスケールは横軸の10倍です） 双曲距離hで測ると、円板の内部のどこから出発しても、円板の縁(E = 1)に近づくとき、歩んだ距離は無限大へとなります。
[2]: モデル上の双曲距離(hyperbolic distance on the model)です。 モデルは無限大を含めた一種の圧縮器ですね。