双曲的非ユークリッドの世界では角と距離とが依存しあいます。 それを平行角の公式で見てみます。
平行角の公式は、

でした。 dは平行線間の双曲距離で、kは距離dの単位のとり方によって定まる定数です。 eは選べる定数です。 これらと平行角![]() について見ていきます。
について見ていきます。
式(1)でeを自然対数の底にとり、kを1にとることを規格化といいます。 今後とくに断らないかぎり、規格化したものだけを扱っていきます。
k = 1 といっても、そのkが1メートルを指す現実の生活空間だとすると、どんな事態なるか想像できますか? もし、kが1兆光年だとすると、私たちが眺めるすべての天体の彼方を含めて、ユークリッド空間だといってもよいでしよう。
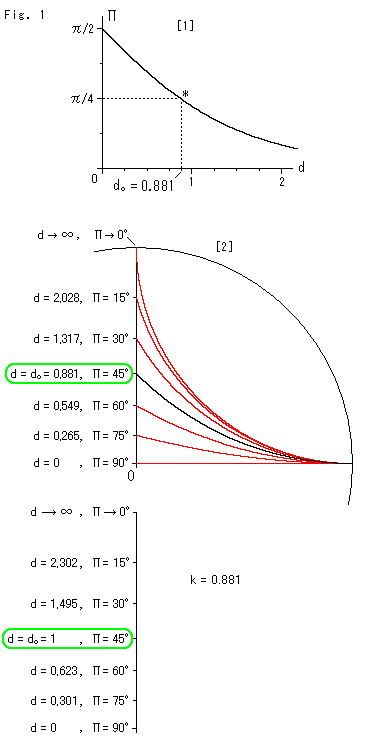
Fig.1をご覧ください。
平行角の公式で長さと角の依存関係を見てみます。 ここでは距離といわずに「長さ」ということばをつかっていきます。
[1]: 長さdと角![]() の関係し合っている様子です。 *印は、平行角
の関係し合っている様子です。 *印は、平行角![]() が
が![]() /4のところです。 そのとき、長さdは
/4のところです。 そのとき、長さdは![]() (= 0.881)です。
(= 0.881)です。
[2]: 角![]() は長さdの測られる直線となす角ですから、ポアンカレ円板の第1象限をつかって描きました。 曲線はすべて平行線です。 黒い曲線は、平行角
は長さdの測られる直線となす角ですから、ポアンカレ円板の第1象限をつかって描きました。 曲線はすべて平行線です。 黒い曲線は、平行角![]() が
が ![]() /4 のときのもので、[1]の*印のところにおけるものです。([1]と[2]の縦軸が
/4 のときのもので、[1]の*印のところにおけるものです。([1]と[2]の縦軸が![]() に関して上下逆になっています。)
に関して上下逆になっています。)
このように、双曲的非ユークリッドの世界では、角がきまれば長さがきまり、長さがきまれば角がきまります。 ですから、前にちょっとふれた長さの絶対単位が自然に定まります。 たとえば、![]() を単位の長さとすることができ、それは幾何学的な意味を持っています。
を単位の長さとすることができ、それは幾何学的な意味を持っています。
もし私たちの住む現実の空間が双曲的であって、実測によって距離dと平行角![]() を得ることができれば、実効あるkの値を見出すことができます。 それができたなら、仮に
を得ることができれば、実効あるkの値を見出すことができます。 それができたなら、仮に ![]() =
= ![]() /4 を単位(基準)とすれば、それに対応する
/4 を単位(基準)とすれば、それに対応する![]() を長さの単位にとるのが至当ですね。
を長さの単位にとるのが至当ですね。
[3]: k = 1 と決めつけて(規格化して)すすめてきたのですが、dの代わりにd/kとして、k = 0.881 にとると、![]() が45
が45![]() のときの
のときの![]() がちょうど
がちょうど ![]() = 1 になります。
= 1 になります。
ボヤイとガウスは、kをどんな値にとるかによって数学的な無数の幾何があるが、現実の空間ではその値が定まっているにちがいないと考えました。 そして、長さの絶対単位が見出されないかぎり、双曲幾何は完成しないと悩みました。
今日、数学者たちは、このことにまったく興味がありません。 物理的な空間には関心がないのです。 ロバチェフスキーも、ほとんど危惧しませんでした。 私たちも、長さの絶対単位ということに捉われないようにします。 でも、それは物理的空間ということとは別に、とても魅惑的な考えですね。 長さの単位が、双曲的非ユークリッドの世界では幾何学的な意味をもったものとして定めることができるのですから。 もっとも、それを定めたからといって、目新しいことが出てくるわけではありません。
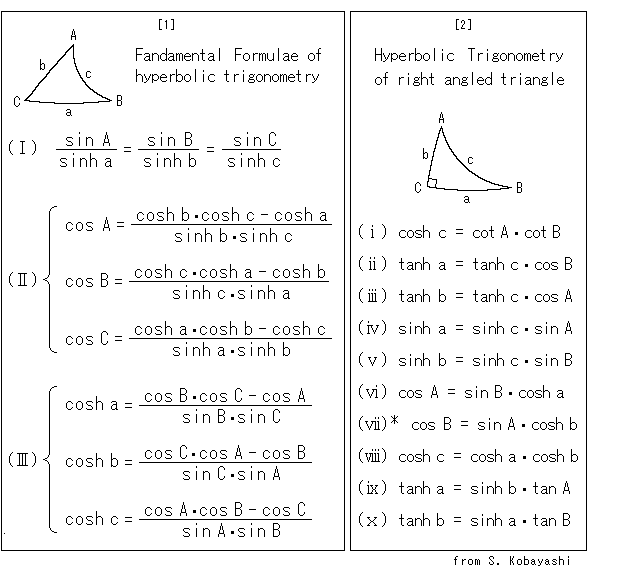
左の2つの囲みは双曲三角法(hyperbolic trigonomrtry)の公式です。 ふつうの三角法と同様に双曲三角法においても、辺や角がゼロのときは適用できない場合があります。 辺の長さが無限大へと伸びているときも同様です。
[1]: 基礎公式(Fandamental Formulae)です。
(![]() )は、ユークリッド三角法の正弦定理に似ています。 球面三角法のとは、さらによく似ています。
)は、ユークリッド三角法の正弦定理に似ています。 球面三角法のとは、さらによく似ています。
(![]() )は、ユークリッド三角法の余弦定理に似ています。 これも、球面三角法のとは、さらによく似ています。
)は、ユークリッド三角法の余弦定理に似ています。 これも、球面三角法のとは、さらによく似ています。
(![]() )は、角だけで辺の長さが定まるという驚異の公式です。 これは、平行角の公式(1)のように1つの角と1つの距離の関係式にはなっていません。
)は、角だけで辺の長さが定まるという驚異の公式です。 これは、平行角の公式(1)のように1つの角と1つの距離の関係式にはなっていません。
[2]: とくに直角三角形(C = ![]() /2)である場合の主な公式です。
/2)である場合の主な公式です。
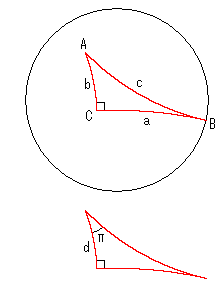
a,cがあらわになっていない*印をつけた![]() に注目します。 右図のようにポアンカレ円板上に直角三角形ABCを描きます。 頂点Bは円板の周上にとってあるので、2辺a,cは平行です。 そして B
に注目します。 右図のようにポアンカレ円板上に直角三角形ABCを描きます。 頂点Bは円板の周上にとってあるので、2辺a,cは平行です。 そして B ![]() 0 ですから B = 0 だとして、式
0 ですから B = 0 だとして、式![]() を適用すると、
を適用すると、
を得ます。 角Aは平行角になっているので、
Aを![]() に、bをdに書き換えて移項すると、
に、bをdに書き換えて移項すると、
となります。 これは、角![]() と距離dの関係ですから、平行角の公式(1)を規格化したものと一致するにちがいありません。
と距離dの関係ですから、平行角の公式(1)を規格化したものと一致するにちがいありません。
それを確かめます。 式(1)を規格化して、K = 1 に、e = 自然対数の底(base of natural logarithm)にした

の両辺のそれぞれを自乗して
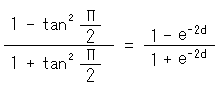
に当てはめると、
となります。 eが双曲線関数tanhに包み込まれて表面から姿を消しました。
これを変形すると、
つまり、 ![]()
となるります。 sin ![]() も cosh d も正ですから、両辺を開平すれば式(2)が得られます。 したがって、式(1)と式(2)は規格化のもとで同値です。
も cosh d も正ですから、両辺を開平すれば式(2)が得られます。 したがって、式(1)と式(2)は規格化のもとで同値です。
かくて、ロバチェフスキーの辿った道を手繰ることなく、モデル上での計算もせずして、平行線角の公式を納得することができました。
双曲三角法の公式は、ロバチェフスキーらが導き出したものですが、むろんモデルによっても証明できます。
ところで、kやeによってモデルにどんな影響を与えるのでしようか? kやeが異なっても、距離のスケールが違ってくるだけです。 kとeと平行角![]() の間には依存関係がありますが、描かれる曲線のパターンには見た目に変化がありません。
の間には依存関係がありますが、描かれる曲線のパターンには見た目に変化がありません。
k,e,![]() の三者の関係を見るには、 [k,eと平行角] をクリックしてください。
の三者の関係を見るには、 [k,eと平行角] をクリックしてください。