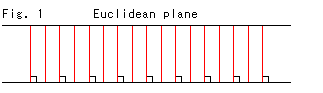
Fig.1は、ふつうの平行線です。 ユークリッドの世界では、等距離線と平行線は同じですが、双曲的非ユークリッドの世界では違います。 等距離線とは、一つの直線から一定の間隔をたもっているものです。
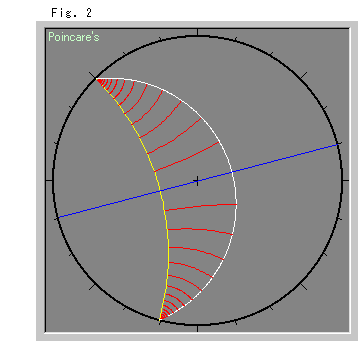
Fig.2をご覧ください。
ポアンカレ円板上の等距離線です。 白い曲線が、黄色い直線に関して等距離になっています。 赤い線分は、黄色の直線だけに直交して、等間隔に並べてあり、すべて同じ長さです。 青い直線は、観察の便だけのものです。
双曲的非ユークリッドの世界では、等距離線は直線ではありません。 ポアンカレ円板上では円弧に描かれます。
この2本の曲線は、無限遠点でくっついているように見えますね。 どこまで行っても、変わらないはずなのに。 そうです、変わりません。 たとえ無限の彼方でも。 なぜって、2曲線間に等距離なへだたりをもつことが定義ですからね。 でも、どのように見て確かめるのですか? 平行線の場合と同様に、無限遠での様子を自分の目で見ることはできません。
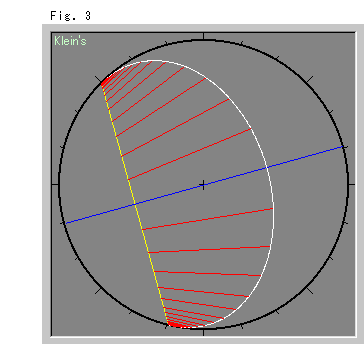
Fig.3は、クラインの円板モデルに描いたものです。 これは、ポアンカレの円板モデルに描かれたFig.2と視覚的な違いをお見せするために、添えたものです。 白い等距離線が、円板の周に内接する楕円の一部になっています。
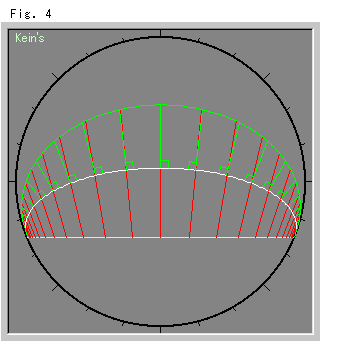
Fig.4をご覧ください。
ユークリッド平面上では、1本の直線に関する2本の等距離線は、等距離線どうしでも等距離線になっています。 双曲的非ユークリッドの世界では、どうでしようか。 図は、曲線と直線の区別が見てすぐわかるクライン円板上に描いたものです。 白い曲線と緑色の曲線は、いずれも黄色い直線の等距離線になっています。 赤い線は、黄色い直線に立てた双曲的法線です。 この二つの等距離線は、どちらも直線ではないので、等距離線の関係にはなりません。 しかし、黄色い直線に立てた赤い法線に沿った白と緑の等距離線間の距離は一定です。
こころみに、白い等距離線上に緑色の法線を立ててみました。 その(双曲的)長さを測ってみると、当然ですが一定ではありません。
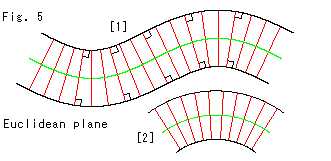
Fig.5は、ユークリッド平面上の平行曲線です。
ちょっと、ついでに平行曲線というのを見ておきます。 それは、2本の曲線がどの点でも共通の法線をもっているものです。
[1]: 赤い線分が共通法線ですが、その長さはかならずしも一定ではありません。
[2]: 同心円の一部です。 この場合はいうまでもなく、赤い線分の長さは一定です。
(画面を上下にスクロールして揺さぶると、平行曲線[1]が身をよじりますよ。)
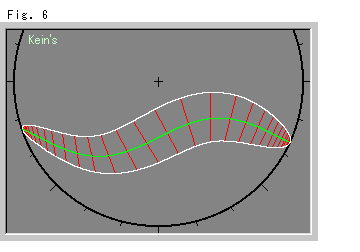
Fig.6をご覧ください。
双曲的非ユークリッドの世界に平行曲線を描くと、どうなるでしようか。 同心円の場合は、ユークリッド平面上と同様ですから、面白くありません。 クライン円板上に、Fig.5の[1]の緑色の線と見た目に同じ曲線を引いきます。 それに双曲的長さが一定な赤い双曲的法線を立てます。 その法線の先端をたどると、白い曲線ができます。 なにか、無限円を食べているいも虫のようですね。 この曲線の接線と赤い法線とは双曲的垂直でないので、平行曲線ではありません。 しかし、図の場合では、ほぼそれに近いものとなっています。 双曲的非ユークリッドの世界では、平行曲線もこのような姿態になるということです。