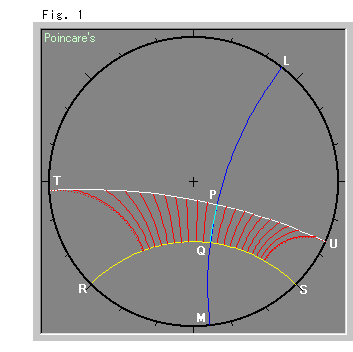
Fig.1をご覧ください。
2本の直線RSとTUは、無限遠(円板の縁)で共有点をもっていないので、双曲的平行線ではありません。 それでいて、交わらずにたがいに離れています。 ユークリッド平面では、平行でもなく交わりもしない2直線はありませんが、双曲的非ユークリッドの世界の平面には、ご覧のようにそれがあるのです。 このような双曲的直線を超平行線と呼んでいます。
ユークリッド平面では平行でない2直線に共通な垂線を引くことはできませんが、これも双曲的非ユークリッドの世界の平面ではできるのです。 ただし、1本だけです。 青い直線LMが共通垂線です。 そんなふうですが、双曲的非ユークリッドの世界の平面ではすぐ後で見るように、平行線に引ける共通垂線は1本もありません。 つまり、ふつうにいう格子線(碁盤の目)は描けないのです。
赤い線は、黄色い直線RSを基準線として、それに垂直に立て双曲的等間隔に並べたものです。 これまでのと同様に視覚の便のためです。
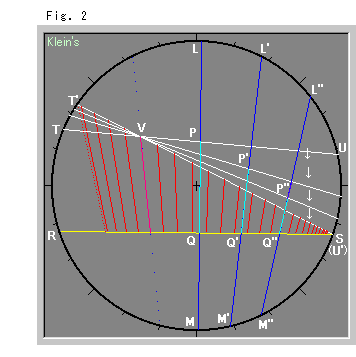
Fig.2をご覧ください。
こんどは、見やすいようにクラインの円板モデルを使います。 直線TUを、その上の1点Vを固定して回転させていくと、共通垂線LMが、L'M', L"M",,,と移動していき、同時に、PQ間の距離dはP'Q', P"Q",,,と小さくなっていきます。 点Uが最終的に点Sと出会い、直線TUが直線T'U'となったとき、共通垂線は、モデル円板の接線になります。 同時に、超平行線間の距離dはゼロになります。 つまり、超平行線がふつうの(双曲的)平行線になるわけで、共通垂線としては消えてしまいます。
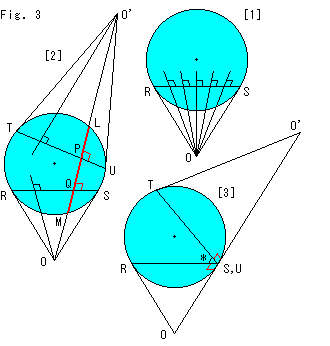
Fig.3をご覧ください。
作図によって、Fig.2の様子を見たものです。
[1]: クライン円板の弦RSの両端R,Sにおける円板の接線ORとOSを引きます。 すると、点Oを通って直線RSを切る直線は、すべて直線RSと双曲的に直交します。
[2]: 与えられた超平行線RS,TUには共通垂線LMが1本引けることがわかります。 点Oを通る直線と点O'を通る直線が一直線になる場合が一つあるからです。 それが一直線O'-L-P-Q-M-Oです。
点O'が点Oと同じ側にくる(超平行線が原点を挟まない)ときも、共通垂線が1本あります。 作図は、接線を用いて同じ要領でできます。
[3]: 弦TUの右端Uが弦RSの右端Sと重なって、2直線RS,TUが平行線になっています。 直線OO'は、直線RSと直線TUの両方に垂直ですが、円板の接線になっていて、その内部を通っていません。 印し"*"をつけた角RS(U)Tはゼロです。 (作図の仕方については、おりおりに触れていきます。)