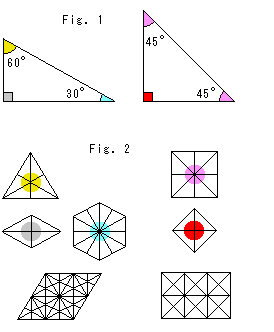
ふつうの平面に合同な三角形でタイル張りができます。 ただし、使えるのはFig.1にある三角定規の2つの三角形だけです。
ユークリッド平面上の三角形の内角A,B,Cは
A + B + C = 
です。 Fig.2のようにタイル張りにするには、1点に同じ角が隙間も重なりもなく集められるので、
でなければなりません。 この自然数
,
,
は、2以上でありさえすればよいではなくして、
,, = 2,3,6 か 2,4,4
に限られます。 なぜそうなのかは、すこし紙細工してみれば解ります。
双曲的非ユークリッドの世界では、
A + B + C <
ですから、
で上式を満たす2以上の自然数,,はいくらでもあります。 それをつかった三角形なら、どんなものでもタイル張りができます。
しかし、角A,B,Cと自然数,,が不可分の関係であり、その角が決まれば辺の長さも決まるので、同じ形の三角形で大きさを選ぶことはできません。
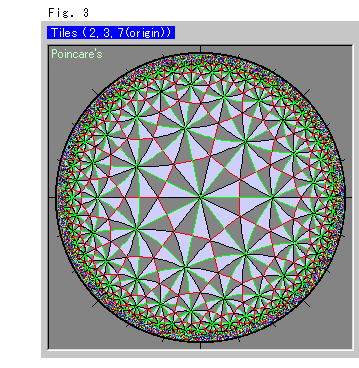
Fig.3の三角形は、 = 2, = 3, = 7 にとったものです。 こんなのを2-3-7三角形ともいいます。 よくテッサレイション(模様)とよばれているものの一つです。 これを見ると、エッシャーの絵を思い出させますね。 彼は画家でしたが、無限の視覚化ということで数学者よりもずっと先を示しました。 その絵は人の心を無限へと惹きこみます。
このFig.3は、双曲的非ユークリッドの世界の線対称ともいえる鏡映を使って描いたものです。 1つの三角形を裏返し、それをまた裏返して（表側になる）と繰り返せば、敷き詰めることができます。 裏返しは、1つの辺を軸として行います。 三角形はすべて合同です。 着色した側を表とすると、無色の方が裏です。
敷き詰めるといっても、2-3-7三角形は有限ですから、永遠に敷きつづけても円板の周まで達することはできません。
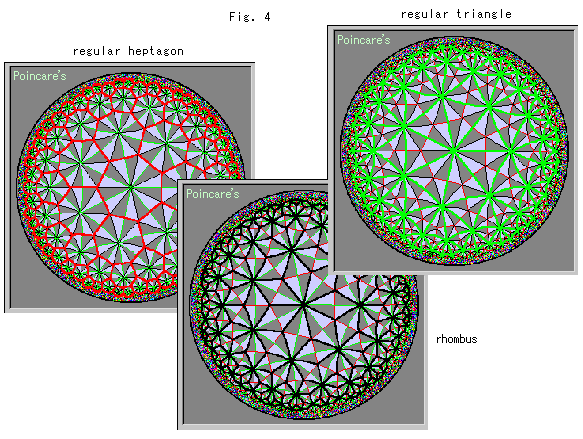
合同な目の網が、2-3-7三角形のタイル張りの中にいくつも見つかります。 Fig.4はその例で、赤いフレームの正七角形(regular heptagon)、緑色のフレームの正三角形(regular triangle)、黒いフレームのひし形(rhombus)です。
実は、円板モデルの周辺近くは、モザイクで誤魔化しましています。 なぜって、パソコンが言うことを聞いてくれないし、仮に聞いてくれても、無限時間かかるからです。
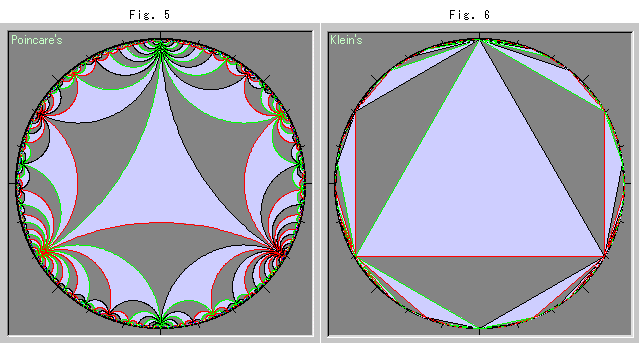
上のFig.5とFig.6は、理想三角形のタイル張りです。 理想三角形というのは、頂点がすべて無限遠へと伸びているものです。 理想三角形の辺の長さは a, b, c 
つまり A, B, C 0 (= 
) です。 そして面積は、 - (A + B +C) となります。
Fig.5はポアンカレ円板のもので、Fig.6はクライン円板のものです。 両者はとても違って見えますが、すべての三角形は合同です。 ポアンカレ円板上の理想三角形の頂点をユークリッド直線でむすぶと、クライン円板上の理想三角形が描けます。
下のFig.7は、作間誠による理想三角形のタイル張りの動画の４コマです。 頂点の1つがモデル円板の赤いスポットの右端に固定されています。 これで見ると、右の3つの図には正三角形らしく見えるものは1つもありません。 けれども、すべて合同です。
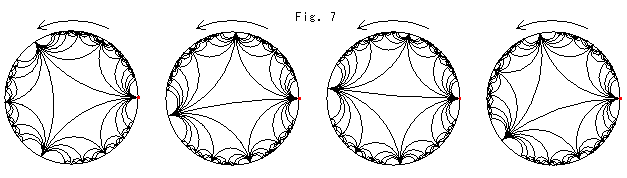
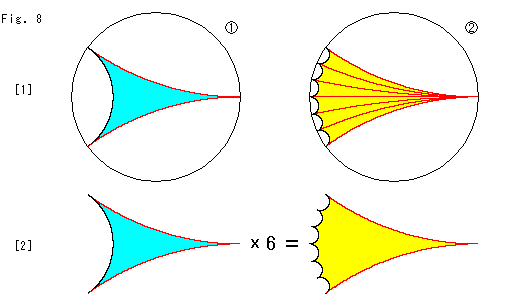
Fig.8をご覧ください。
理想三角形は内角がすべてゼロで、辺の長さは無限大だとして話をします。 その意味で、すべての理想三角形は正三角形です。
[1]: 
は1つの理想三角形です。 
は6つの理想三角形で、一番外側の赤い辺はの水色の三角形の赤い辺と同じです。 理想三角形はすべて合同ですから、の黄色い三角形の一つ一つが水色の三角形と同じです。
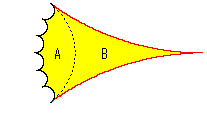
[2]: 面積で見ると、左辺の水色の理想三角形を6倍したものが、右辺の黄色い図形の面積になります。 その図形は、すべての内角が0ですので、ゼロ角7角形とよべます。
それを右図のように点線で切ると、Aはゼロ角6角形で、Bが水色の理想三角形と同じものになります。
理想三角形には双曲三角法を適用できないのがふつうです。 ここでのイラストは、そんなものに頼らなくても、直感的に十分納得できます。 それこそ理想三角形の特徴です。