平行移動は、ユークリッドの世界では、Fig.1のように、図形上のすべての点を平行に同じ距離だけ動かすことです。 そして、平行移動で図形の形や大きさが変わることはありません。 終始、合同です。 双曲的非ユークリッドの世界で、三角形を動かしてみると、どうなるでしようか? 実験してみましよう。
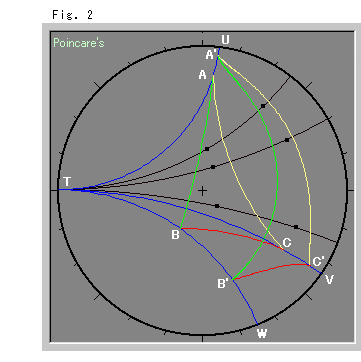
Fig.2をご覧ください。 まず、平行線の上で三角形を動かしてみます。 Tを共有点として、三角形ABCの3頂点を通る青い直線TU,TV,TWを引きます。 黒い平行線は、三角形ABC上の点を通っています。 図には描かれていませんが、三角形ABC上の無数の点のそれぞれを通る平行線があると思ってください。
三角形ABCのすべての点を、それぞれの平行線上で同じ(双曲的)距離だけ動かしました。 見ると、新しい図形A'B'C'は、三角形とは似てもにつかぬ形になっています。 A'B', B'C', C'A'は、もはや直線ではありません。
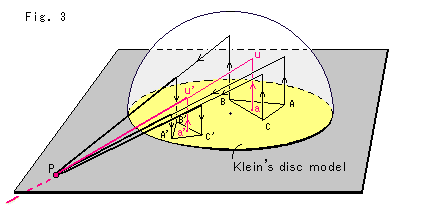
それでは、鏡映をつかって、合同を保つようにしましょう。 Fig.3のように、半球モデルを使います。 黄色い底面がクラインの円板モデルです。
まず、鏡映のための2点a,a'を与えます。 aはもとの三角形ABC上の1点で、a'はその移動先です。 点a,a'から赤い垂線を立て、半球上の2点u,u'を得ます。 この2点u,u'を通る赤い直線は、平面(灰色)を点Pで貫通します。 点Pを鏡映の極といいます。
つぎに、三角形ABC上の他のすべての点を移動します。 黒い線で示すように、たとえば頂点Aを動かすには、半球面まで上って、そこから半球内をくぐって極Pに向かって進むと、ふたたび半球面に達します。 そこで下の黄色い円板へ降りますと、その着地点が移動先の頂点A'になります。(後のほうで、これと同じことを平面上だけで行います。) 鏡映では、図形が裏返りますので、実際には鏡映を2回行います。 ポアンカレ円板上の図形なら、クライン円板のそれに変換して動かしたあと、ポアンカレ円板上に戻します。
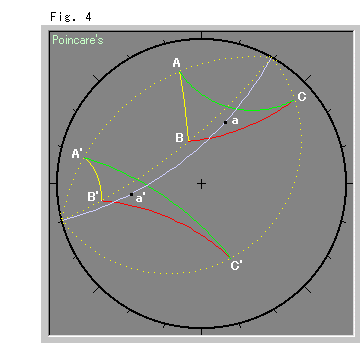
Fig.4をご覧ください。 三角形ABCがA'B'C'へ鏡映(2回)によって動かされています。 黄色い点線は、3頂点の軌跡です。
新しい三角形A'B'C'は、もとの三角形ABCと完全に合同です。 辺の形は変わって見えますが、角は見た目にも保存されています。 軌跡は、直線ではなく等距離線になっています。 等距離線を平行移動用の平行線だと思うのもよいでしよう。 しかし、各頂点の移動距AA',BB',CC'が同じではありません。
それでも、これを双曲的平行移動といってよいそうです。 平行移動については、Ch.17でまた触れます。
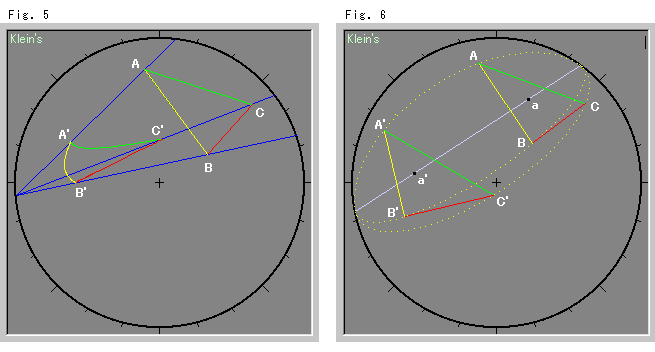
下のFig.5とFig.6は、クラインの円板での実験をやってみたものです。 Fig.5がFig.2の場合で、Fig.6がFig.4の場合です。 Fig.6では、辺の長さも角も変わって見えますが、むろん2つの三角形は合同です。