円は双曲的非ユークリッドの世界でどのようになっているのでしょうか。 半球モデルを使います。
ここでは、半球をモデルとしてそのまま使うことはしません。 それをツールとして半球面上に円をつくり、ポアンカレやクラインの円板に射影するのに利用します。 ポアンカレ円板への射影には、半球でなく、球を使います。また、ここでは有限半径の円だけをとりあげます。 有限半径の円は、円周が無限遠(円板の縁)に触れないものです。
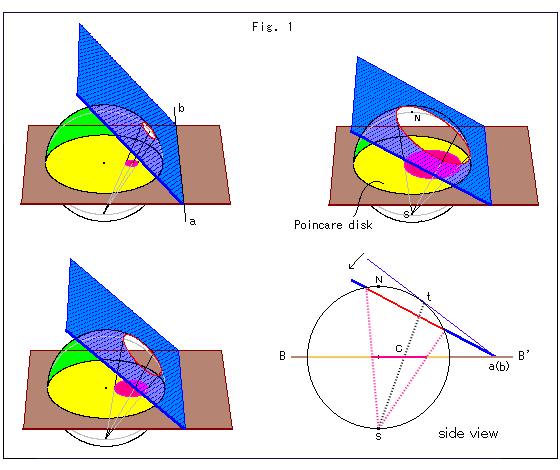
上のFig.1をご覧ください。
黄色いところがポアンカレ円板で、茶色の赤道面上にあります。 青い平面は、赤道面上の直線abにヒンジ留めされていて、半球(球の上半分)をスライスします。 便宜上、青い平面をスライサーと名付けておきます。 球の半径は無限大です。
スライサーは半球面に円形の切り口をつくります。 その円は南極Sに射影され、そのとき黄色いポアンカレ円板の中に赤い円を形成します。 右下の側面図(side view)は、赤道面BB'を水平にしてヒンジ軸abの方向から見たものです。 点tは、スライサーが左へ傾いて最初に半球に接したところです。 赤い円の双曲的中心は、黒い点線の射線tSと赤道面との交点(貫通点)Cです。 この射線tSは、ヒンジ軸abを固定してスライサーが左へ傾けるときは、変化しません。
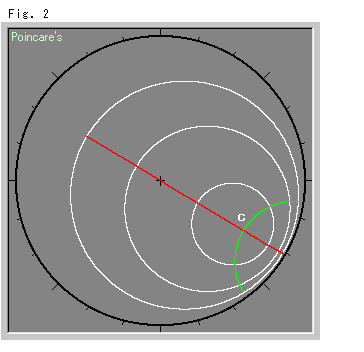
Fig.2をご覧ください。
ヒンジ軸abを固定しておいてスライサーの傾きを変えてみたときの様子を真上から見たものです。 Fig.1の黄色いポアンカレ円板を黒で、その上の赤い円を白で描いています。 円の中心Cは動かずに、同心円になっています。 各円の半径が 0.5, 1, 1.5 となるようにスライサーを傾けました。 赤い直線と緑色の(双曲)直線は、たがいに直交する1組の直径で、赤い方は見やすいように原点を通るものを選んでいます。
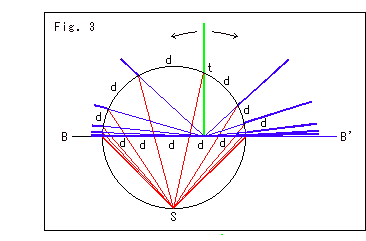
Fig.3をご覧ください。
ヒンジ軸abを球の中まで入れてみます。 今度は、スライサーの傾きを変えたのを同時に描きました。 緑色のは、スライサーが垂直になているものです。 スライサーの傾きは、球面上を点tから等間隔d(0.5, 1, 1.5,,,)にとってあります。 それで、赤い射線が赤道面BB'を貫通する点の間隔もdになっています。

Fig.4は、Fig.3を上から見たものです。 白い曲線は、赤い射線が赤道面BB'を貫通した跡です。 緑色の曲線は垂直な緑色のスライサーに、白い曲線は傾いた青いスライサーに対応しています。 これらの曲線と赤い水平な直線との交点は、Fig.3の赤い射線と赤道面BB'の交点に対応しています。 白い曲線は、緑色の曲線に関して距離dの等距離線になってます。
Fig.2の同心円を、中心Cに関する等距離線だととらえると、Fig.4で等距離線が出てきたのも肯けますね。
それでは、ヒンジ軸abが球の周に接するときは、どうなるでしょうか? それは、あとで見ることにします。
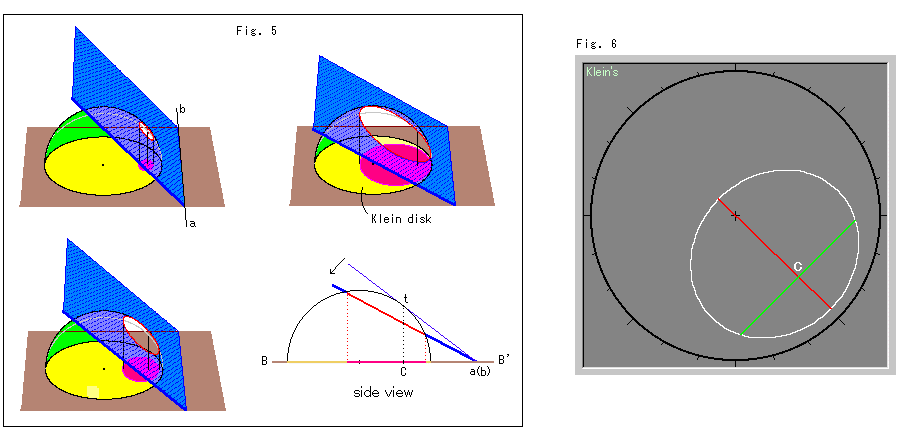
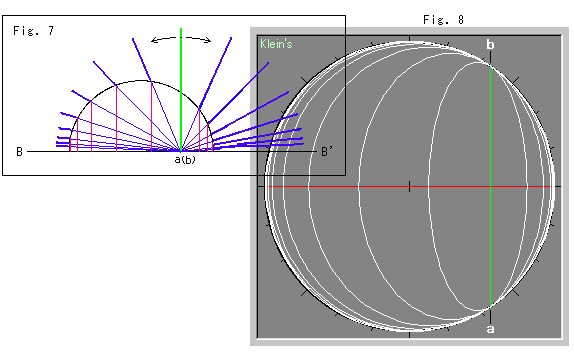
下のFig.5〜Fig.8は、クラインの円板モデルと見比べるために描いたものです。 スクロールして、見てください。