双曲的非ユークリッドの世界の中で、円を動かすとどうなるでしょうか。 ただ動かしただけで、円自体が変化することはありませんが、モデル上の見た目に映るものは大きく変わります。
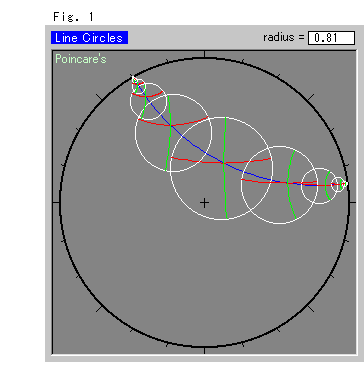
Fig.1をよくご覧ください。 青い線は直線です。 図は、その直線上を動いた円をたどったものです。 赤と緑の線は、たがいに直交する直径で、その交点は円の双曲的中心です。 赤い直径は、意図的に中心で水平となるように描かれています。 円の中心間隔は一定です。
円が原点から離れるほど、その中心はモデルのふちの方へ偏っていき、円は小さくなって見えます。
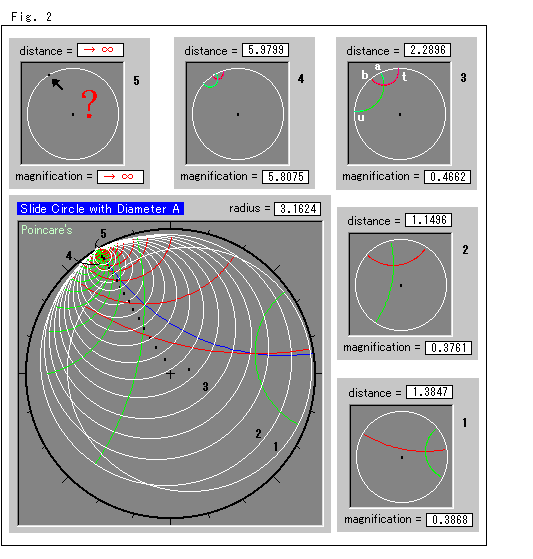
Fig.2をご覧ください。 この図は直径が連続的に変わる様子をとらえようとしたものです。 周囲の小さな図は、スナップショットです。 各図に示されている距離(distance)は原点から各円の中心までの双曲距離です。 拡大率(magnification)は、視覚的にも変わらぬ大きさを保つようにしたものです。 ただし、円全体が無限遠へ向かったときには、拡大率を無限大へと大きくしなければならないことになり、赤と緑の直径は円周上の1点に重なろうとします。 黒い→の先は、その1点です。 しかし、果たしてこれでよいのか断言はできないので、“？”を添えておきました。 円の間隔は、一定ではなく、見やすいようにとってあります。 黒いスポットは、視覚上の中心です。
右上隅の小さい図3を見てください。 白い円周上の、弧aｂ(小さく見える方)の長さと弧tu(大きく見える方)の長さは、双曲的に同じです。
そして、二つの弧は、双曲的中心から見た同じ中心角
/2をもっています。
真上の小さい図4では、赤と緑の直径がずいぶん小さくなって見えます。 でも、それらは実際の直径です。
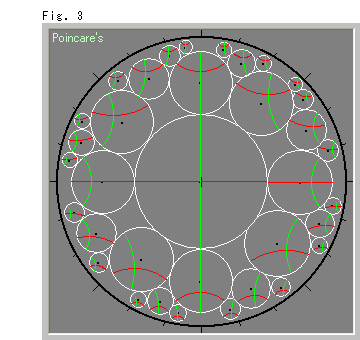
Fig.3をご覧ください。
双曲平面上のさまざまな点で、そこの住人Aが半径1の周囲を見渡したときの様子を私たちのポアンカレ円板で見たものです。 すべての白い円は、もちろん合同です。 A氏の心になってみると、方位はどこへ行っても変わりません。
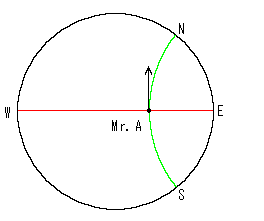
足元の直下と周囲では方位が異なるよに思えますが、そうではありません。 A氏から見た北方Nの方向は矢印のようにつねに真っ直ぐ上の方です。 東西南北いずれの方向についても同様です。 つまり、私たちと同じです。 点NからA氏の方へ光線が曲がって伸びるのだと思ってもよいでしよう。
しかし、長さについては私たちのとは著しく違います。 双曲半径1の円周の長さは、2
の1.1752 (= sinh 1) 倍です。