円板モデルは、前に見たように、すべての点が全方向から圧縮されています。 ここでは、その逆をしようとするのです。 円板モデル上のすべての点の近くを右図のように押し広げれば、実際の双曲的平面になります。 しかし、そうしたのでは鞍形に波打たものになってしまいます。 (波打たせても、実際の双曲平面にはなりません｡) あくまで平面のままで行います。 ですから当然、双曲平面として正しいものではありません。 しかし、傾向的なことを知る上では、役立ちます。
後半では、円板モデルを伸張せずにそのままで圧縮されている様子を見ます。
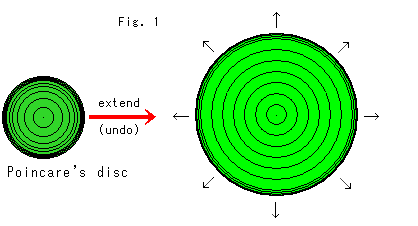
Fig.1をご覧ください。
ポアンカレの円板モデルでは、双曲的非ユークリッドの世界をどれくらい圧縮しているのでしょうか。 図はポアンカレ円板を四方八方に引っ張って、モデル上の同心円の間隔を等間隔にしようとしているところです。 半径方向はよいのですが、同心円の円周の長さが、これでは双曲平面のそれと一致しません。
Fig.2のような半径方向(ray-direction)と円周方向(circuit-direction)の２方向へモデルを引伸ばします。 円周方向というのは、円周に乗った方向で、円の接線の方向ではありません。
双曲的非ユークリッドの世界では、円周率は一定値
ではありません。 円周は
双曲円周 = 2 sinh r (r = 双曲半径)
です。 この式を変形して
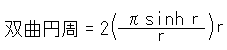
とします。 そして、括弧内を双曲円周率とよんで、
と表すことにします。
です。
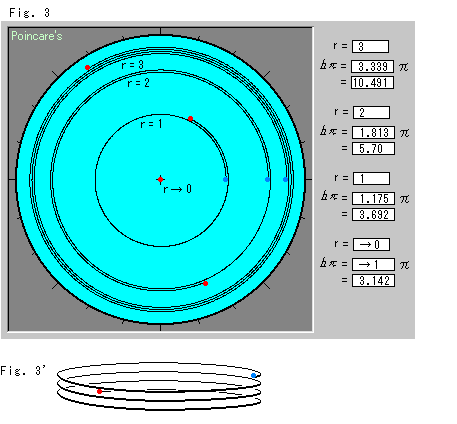
Fig.3は、原点を中心とする同心円の各円周を見た目にも実際の双曲円周の長さになるように円周方向に引き伸ばしたものです。 渦巻きにして表現しています。 渦巻きは何重になっても実際には厚みはないのですが、それとわかるように描いています。 双曲半径rが大きくなると、双曲円周率が急激に大きくなります。 双曲半径rがゼロに近づくと、双曲円周率はふつうのにほとんど等しくなっていきます。
Fig.3'は、渦巻きの1つをコイルにして表現してみたものです。 こんなふうに、モデルの面は1つだけれども、潜っていくようになっているのだと思ってもよいでしよう。（無理に1つの面にすると、波打ってしまいます｡）
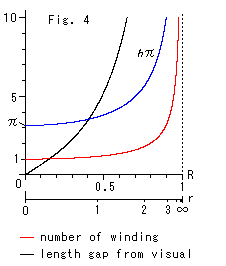
Fig.4をご覧ください。 Rはモデル上を目で見た原点からの距離(同心円の半径)です。 双曲半径rは半径Rに対応しています。
青い曲線を見ると、双曲円周率は半径Rに関して急速に大きくなるのがわかります。
赤い曲線は、渦巻きの巻き数(number of winding) sinh r / r です。 たとえば、r = 3 (R = 0.905) のときの巻き数は、3.339 です。 この数値は、Fig.3の右上にあるのと同じです。
黒い曲線は、双曲円周 2 sinh r とモデル上を目で見た円周 2R との差です。
双曲的非ユークリッドの世界では、半径が 1m, 2m, 3m だと、円周はそれぞれ 7.38m, 22.8m, 62.9m になります。 これくらいだとよいのですが、半径が100mになると、円周は天文学的な8.4x
mにもなってしまいます。 1光年が9.4x
mですから、想像してみてください。
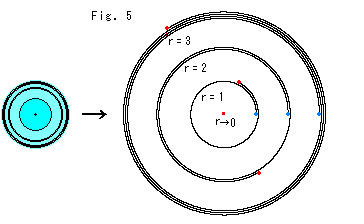
Fig.5をご覧ください。 モデル円板を小さく描きます。 そして、円板モデルはそのままにしておいて、渦巻きだけを見た目にも双曲半径になるように半径方向にも引き伸ばします。 渦巻き以外のところは、何も意味していません。 半径1の渦巻きがモデル円板のと同じ大きさに描かれてあるのは、モデルの作図半径も1にとってあるからです。
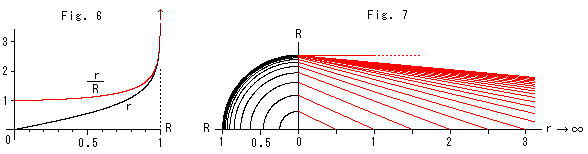
下のFig.6とFig.7は、モデル円板上の目で見た原点からの距離Rと、その実際の双曲距離rの関係です。
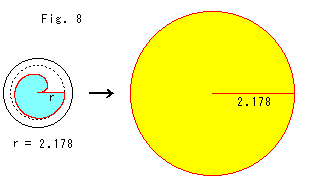
上のFig.5の渦巻きを周とする面をつくろうとすると、スクリュー状のものになり、重なったところができてしまいます。 それで、このFig.8の空色の形のようにモデル円板をくり抜いて、円周方向と半径方向に引伸ばすと、黄色い円ができます。 この黄色い円の内部では、円周方向と半径方向だけの距離は、空色の円板モデルの内部での実際の双曲距離になっています。 しかし角は、かえって実際と異なってしまっています。 黄色い円板が本当の双曲平面ではないからです。
角に関しては、ポアンカレのモデルでは見た目にも変わりはないのですから、引伸ばしは必要ありません。
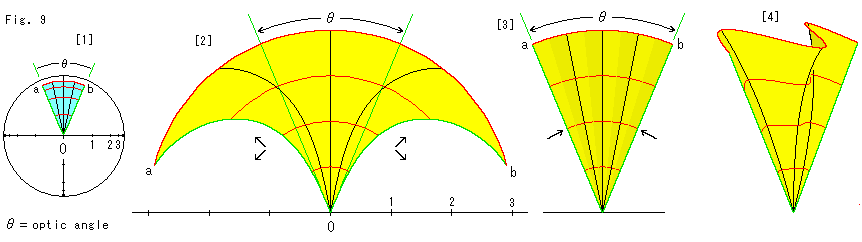
上のFig.9をご覧ください。
これもFig.8と似た考えです。
[1]: ポアンカレ円板上の扇形aObです。 
は原点Oから見た視角(optic angle)です. ポアンカレ円板ですから、はそのままで双曲的角と一致しています。 この扇形aObを切り取ります。
[2]: そして、円周方向と半径方向に引伸ばすと、黄色いイチョウの葉のような形が得られます。 半径方向を実際の双曲的長さにします。 赤い円弧も実際の双曲的長さにしたので、視角からはみ出してしまっています。 光線が黒や緑の曲線のように進むのならよいのですが、そうはいきません。 しかし双曲平面上では、赤い曲線の長さのものが視角内に見えるのです。 光線が曲がって目に入ってくるのではありません。
[3]: そこで、両側から絞って全体が視角内に入るようにします。 むろん、そのために平面を保つことができずに、皺がよります。
[4]: [3]をすこし傾けて斜めから見たところです。 大きく波打っています。
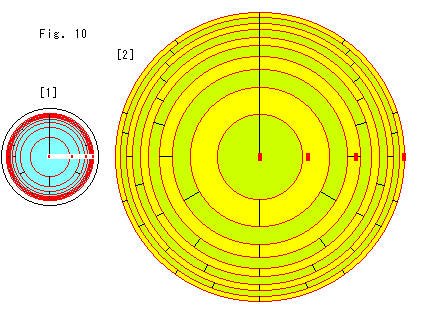
Fig.10をご覧ください。
こんどは切り取らないで、半径方向へだけ引伸ばします。
[1]: 円板モデル内の赤い同心円の最大半径は、双曲距離3です。 最大半径を制限したのは、大きくとると実際の双曲距離してみようとすると、描き切れなくなるからです。 よこに並んでいる4つの赤い印しは、原点から双曲距離1の等間隔にとったものです。
[2]: 円周方向と半径方向に引伸ばしたものです。 円周方向に伸ばしたことの描画に工夫してあります。 赤い同心円の間の色を交互に変えてあるのは、見やすくするためです。 それらを仮にベルトとよんでおきます。 赤い同心円は、円周方向の実際の双曲距離が見た目の 2, 3, 4,,,倍になるところを通る円からなっています。 各ベルトの外縁は、内縁より実際の双曲距離が、(円周方向に引伸ばした場合）1円周分多くなっています。 それをベルト上の黒い仕切り線で表わしています。 1つのセクター(仕切りと仕切りの間)は、実際の双曲距離になるように円周方向に引伸ばせば、内縁で測った1円周分になるものです。
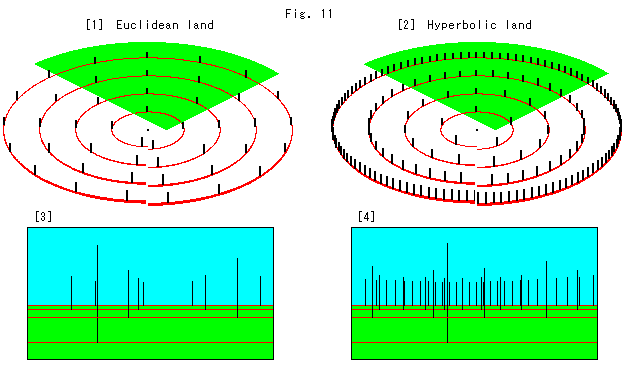
上のFig.11をご覧ください。
[1]: ユークリッド幾何が機能する平坦な地面です。 原点を中心にとった同心円のそれぞれの円の向こう側から左右に、円周に沿って等間隔に柱が立っています。 等間隔の巾は、どの円でも同じです。 円周のこちら側が切ってあるのは、連続して等間隔に柱を立てることはできないからです。
[2]: 双曲的非ユークリドの世界の平面です。 そこでは、双曲幾何が支配しています。 ただし、半径方向は双曲距離の通りですが、円周方向は圧縮して描かれています。 そのため、柱は、[1]と同じ間隔で並んでいるのですが、大きい円周になるほど建て込んでいます。 建て込まないようにするには、鞍形の曲面にするか、圧縮した物差しを使用するほかありません。 この物差しは、円周に合った円弧になっていて、原点から離れるにしたがい、目盛りが縮んでくるものです。
[3]: 原点の近くから[1]を写真を撮ったとした絵です。 [1]の緑色の扇形が、カメラの視野です。
[4]: 同様に[2]を写真を撮ったとしたものです。
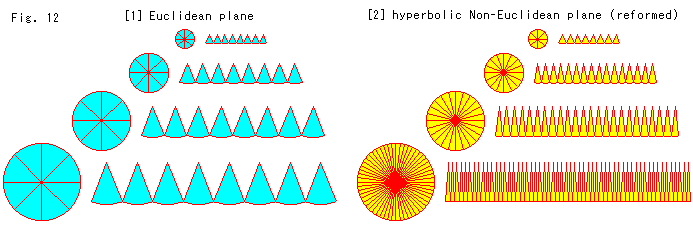
上のFig.12をご覧ください。
[1]: ユークリッド平面(Euclidean plane)上の円を扇形に切って並べています。 円の半径は、上から順に半径1,2,3,4にとっています。
[2]: 双曲的非ユークリッド平面(hyperbolic Non-Euclidean plane)を、所要の点において円周方向だけに圧縮し鞍形なるのをさけて、ユークリッド平面に似た扱いができるように改造(reform)しました。 図は、そういう平面上のものです。 そこに[1]と同じ大きさの円を描きます。 円の内部での円周方向の圧縮は、均等になされているものとします。 図は、そんな円から[1]と同じ大きさの扇形を切って並べてたものです。 切り取ったものは、Fig.9のようなイチョウ形ではなく、まともな姿の扇形です。 しかし、各円の中心を中心とする円周方向に圧縮しているので、切り取られる扇形の個数は、円の半径rが大きくなると sinh r で急激に増えていきます。 図の場合、一番小さい r = 1 の円ではあまり変わりはありませんが、半径が2,3,4,,となるにつれて、黄色い扇形の数はおおよそ4,8,12,27,,,となります。
私たちは、無理に平坦な面をつくって、実際の双曲的非ユークリッドの世界(平面)が円板モデルにどの程度に圧縮されているかを見ました。 この圧縮ということを正確につかむには、微視的な見方である計量というものによらなければなりません。
つぎに、ポアンカレの円板モデルそのままで、引伸ばしたりせずに、それが圧縮されている様子を見てみます。
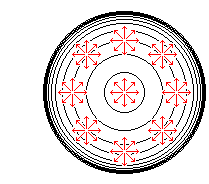
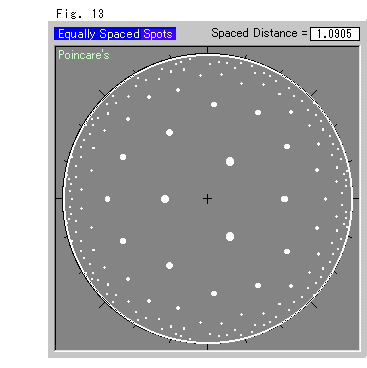
Fig.13は、モデル内に等間隔に置いたスポットです。 スポットの大きさは、すべて同じです。 原点から離れるほど、スポットも間隔も小さく見えてきます。
(スポットを等間隔にとれるパターンは、これ以外にありません。(参照 Ch.12))
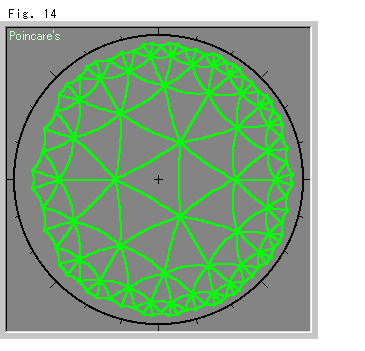
Fig.14は、Fig.13の隣り合うスポットを(双曲)直線でむすんだものです。 網目のそれぞれは、双曲正三角形です。 内角が/7で、1点の周りに7つの双曲正三角形が集まっています。 当然、ユークリッドの世界ではできないことです。
右下のFig.15は、適当な一定領域ごとに一定数のドットをランダムにスプレーしたものです。 こんなのを双曲スプレーとでもよんでおきます。
本当の双曲的非ユークリッドの面が見れるように双曲スプレーを均等に見えるようにすることができればよいのですが、平坦な面の上では不可能ですね。
Fig.16は戯れです。 ポアンカレやクラインの円板を図のように眺めると、遠くが広がって見え、無限遠も見えますよ。