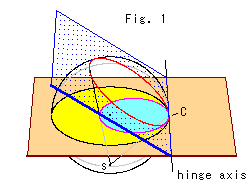
半球モデルの切り口を射影したとき、ヒンジ軸(hinge axis)を半球の外側におくと円を得ましたが、半球の中へ入れると等距離線になってしまいました。 ヒンジ軸をちょうど半球の縁におくとどうなるでしようか？
右のFig.1をご覧ください。 黄色い円はポアンカレの円板モデルです。 上側の赤い輪は、半球の切り口です。 それは南極Sへ射影されて、円板モデル上に空色の円をつくります。 この空色の円は、とても神秘的なので、ホロサイクルと名付けられています。
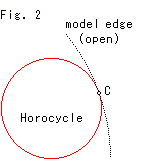
ホロサイクルの中心は、Fig.2のように点C(円板モデルの縁)にあって、そこは無限遠点です。 そして、その円周も点Cを通ります。 つまり、中心が円周上にあるのです！
円板モデルは開領域ですから、ホロサイクルは閉じた円(ループ)にはなっていません。
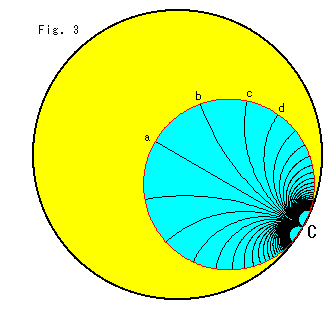
Fig.3は、ポアンカレの円板モデル上のホロサイクルです。 黒い線 aC, bC, cC,,,は、中心点Cから出ている直線で、円周に直交しています。 その長さは無限大です。(点C自体のことは、考えに入れていません｡） すると、
= 
.
と書いてもよいでしよう。
点b,c,d,,,は、観察しやすいように、点aから円周に沿って等間隔にとってあります。 しかし、間隔が何であれ、中心Cに関する中心角はすべてゼロです。
= 0 .
です。 なぜなら、すべての半径が、点Cを共有点とする平行線になっているからです。 しかし、図を見ていると、中心角の和は180
であるように思えます。 ゼロの角を無限個集めると、180になるのかな。 それとも、ホロサイクルは中心のない円なのかな？ そんなものを円とはいえないし。 いやいや、ホロサイクルをふつうの円のように扱ってはなりません。 ホロサイクルでは、ふつうの“中心角”という概念は通用しないのです。
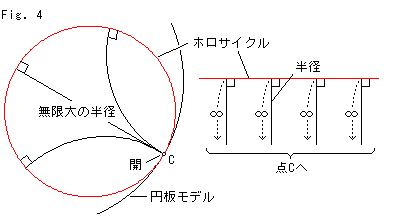
Fig.4をご覧ください。
ホロサイクルの半径は無限大で、すべて1点C(中心)へ伸びています。 ロバチェフスキーの考えた極限円と同じものですね。 ですから、ホロサイクルは円でありながら、ふつうの直線のような性質ももっているわけです。
頂点の1つが無限遠である三角形には、双曲三角法が適用できません。
Fig.5をご覧ください。
ポアンカレ円板上に等距離線を描いたものです。 緑色の直線(円弧)が基準線で、その等距離線が赤い曲線(円弧)です。 点Pを等距離線が通る点として固定しておいて、緑色の基準線を矢印のように円板の縁の1点Cへ近づけていきます。 すると遂には、基準線は点Cになってしまい、赤い等距離線は円板の縁に接する円、つまりホロサイクルになってしまいます。
なにしろ、円でもあり直線でもあるというホロサイクルは二重人格者ですからね。 また、あとでふれる射影幾何で見ると、ホロサイクルは無限遠直線(円板の縁)に接しているので、放物線ともいえます。
等距離線に沿った動きは平行移動であることをCh.13で見ました。 それでは、ホロサイクルに沿った動きは、どうなるでしようか。
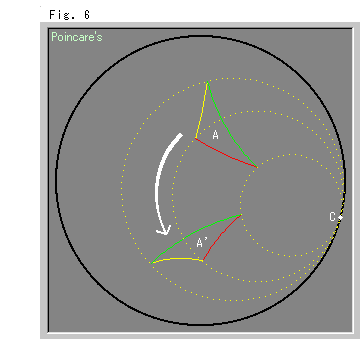
右のFig.6をご覧ください。
三角形Aをホロサイクルに沿って鏡映(2回)で動かしています。 三角形Aと三角形A'は合同で、双曲的平行移動になっています。 各頂点と点Cの間の双曲距離は無限大ですが、それを不変な一定のものとみると、双曲的回転移動ともいえます。
回転移動といっても、三角形が点Cのところを連続して通過できるのかどうか、まだわかりません。 三角形は、点Cへ来ると1点になるのでしようか、それとも一瞬姿を消すのでしようか？ それに、平行移動と回転移動が同じとは、まことに奇妙ですね。
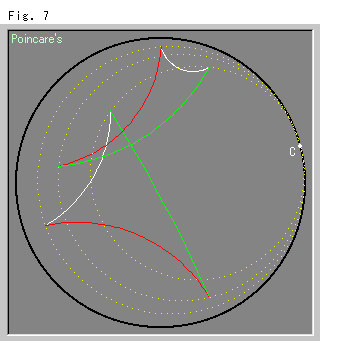
Fig.7をご覧ください。
これはFig.6と同様ですが、大きい三角形を選んで動かしてみたものです。 移動の前後で形も大きさも変わって見えますが、ずっと合同です。 ホロサイクルは、ここでは同心円です。
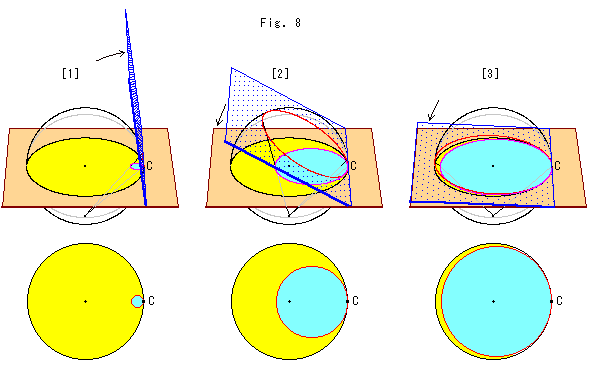
上のFig.8をご覧下さい。
ヒンジ軸を半球の縁に固定して、スライサーを回してみます。
[1]は、スライサーを起こしたところです。 スライサーを垂直に立ててしまうと、水色のロサイクルは1点Cになってしまいます。
[2]は、スライサーをねさせたところです。 ホロサイクルが大きくなっていきます。
[3]は、スライサーをもっと横にして、水平近くにしたところです。 スライサーを水平にしてしまうと、ホロサイクルは黄色い円板モデルと同じになります。 しかし、その中心Cは、つねにスライサーと半球のもとの接点Cに留まっています。
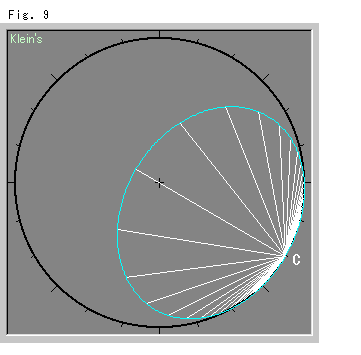
Fig.9は、双曲直線もふつうの直線として表わされるクラインの円板モデルに描いたホロサイクルです。
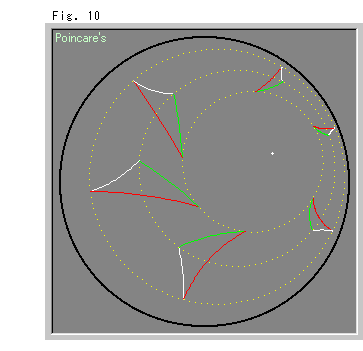
右のFig.10は、中心(白いスポット)をポアンカレ円板の内部においた同心円の上での三角形の回転移動です。 ホロサイクルのFig.6やFig.7と見比べてください。