実際の双曲的非ユークリッドの世界(平面)を、そのまま見せてくれるベルトラミーの擬球とよばれるものを見ていきます。
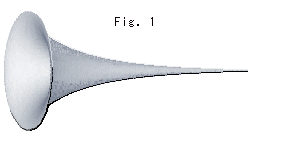
擬球は、Fig.1のようなラッパに似た形の面で、無限に細長い尻尾がついています。 この面を平面と見立て、測地線を直線だとすれば、双曲的平面の一部になるのです。
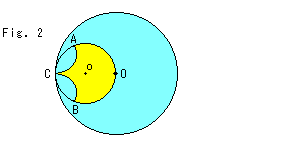
Fig.2をご覧ください。
ポアンカレ円板モデルから擬球をつくってみましよう。 大きな円Oが円板モデルです。 小さな円oは円Oの半径OCを直径としています。 点Oは円板モデルの原点(中心)で、点Cは円板モデルの周上(無限遠)にあります。 つまり、円oはホロサイクルです。 点Cは、円板モデルの周上のどこにとってもかまいません。 円oの内側の円弧ACとBCは、円oに直交しています。 円弧AOBの双曲的長さは、2
にとってあります。 この円板モデルから黄色い扇形をくり抜きます。 (この扇形もイチョウの葉の形をしていますが、Ch.16で見たイチョウ形とは全く別物です｡)
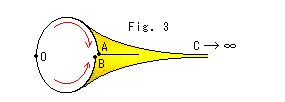
くり抜いたものは柔らかなものだとします。 そして、その上の長さがふつうに測って実際の双曲的長さになるように引き伸ばして、ACとBCを貼り合わせます。 すると、Fig.3のように、ラッパのようになります。 双曲平面であるモデル上から私たちのユークリッド空間の中へ取り出せば、バネ仕掛けのように自動的にくるまって、尻尾を無限遠へと突き出していくと思ってもよいでしよう。
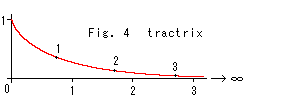
Fig.4は追跡曲線(tractrix)といわれるもので、擬球はこれを母線とする回転面です。 曲線上の数値は、開広部(左端の縁)から母線に沿った距離です。
こうしてできた擬球上で、
測地線(最短距離の道)を直線だとして、曲面を平面だと見立てる
という約束をします。
すると擬球は、完全な双曲的非ユークリッドの世界(平面)をユークリッドの世界の中に再現するものとなります。 そこでは、特別な物差しも特別な分度器もいりません。 まったく、見たとおりです。 なんと素晴らしいではありませんか！
下のFig.5をご覧ください。 点Cから放射状に出ている曲線はすべて双曲的直線です。 同心円のように見える曲線は、間隔を0.5にとった等距離線です。 双曲的直線ではありません。 円弧AmOm'Bの双曲的長さは、2にとってあります。 点m,m'は、それぞれ円弧AO,OBの中点です。 扇形の暗く描いてある部分は、擬球の向こう側との対応を見やすくするためです。 三角形は、擬球上との対応例を見るために描いたものです。
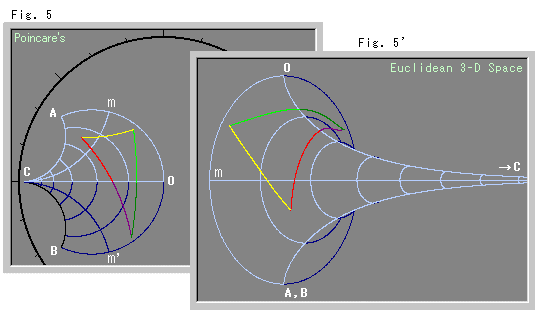
Fig.5'は、Fig.5からつくった擬球です。 擬球の最大半径は1になっています。 (Fig.5'の描画スケールはFig.5より小さくとっています｡) 輪切り線のように見えるのは、Fig.5の同心円に対応していて、擬球面に沿ったふつうの距離で等間隔0.5になっています。
擬球上では三角形が大きく見えますが、角も長さもFig.5と変わっていません。 Fig.5'では、実際の双曲距離で描かれています。
ポアンカレの円板をつかいましたが、クラインの円板でもFig.5'とまったく同じ結果が得られます。
残念なことに、双曲的非ユークリッドの世界全体、つまりモデル円板の全体を擬球に写すことができません。 とくに、モデル円板の原点Oの周辺を一度に写せないのが惜しい。 ヒルベルトが、その不可能なことを証明したそうです。
下のFig.6をご覧ください。
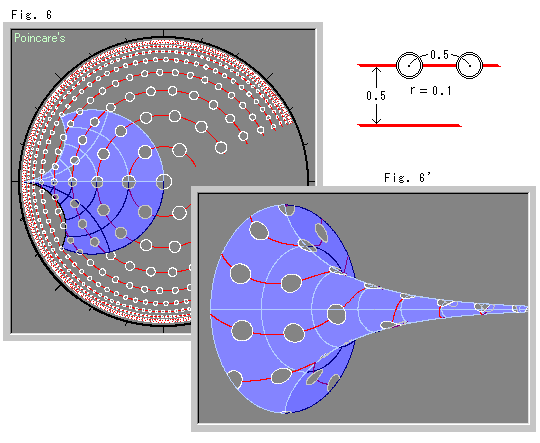
擬球が双曲的非ユークリッドの世界の平面を見せてくれるものであることを確かめましょう。 円板モデル上に赤い双曲同心円を描き、その各円の上に小さな白い双曲円を等間隔に並べます。 赤い同心円の各半径の間隔は0.5です。 白い円はすべて、半径0.1で、赤い同心円上の間隔は0.5です。 等間隔に並べて１周すると、最後のところが等間隔になりませんので、右の方は省いています。 そうしておいて、擬球にするところを切り抜きます。
Fig.6'は、できた擬球です。 見ると、赤い円はまさしく等間隔の同心円になっています。 白い円は、すべて同じ大きさになって、同心円の上にふつうの等間隔に並んでいます。 それぞれの白い円が小さな鞍形になっています。
円板モデルからの切り抜きは、Fig.7のような非対称な形でものでもかまいません。 いっそ、右のFig.8のように、くり抜く範囲を大きくとります。 そして、ぐるぐる巻きのままで、見たいところだけを照明してもよいですね。 このように多層面(multi-layer)になっている擬球を多層擬球とよんでおくことにします。
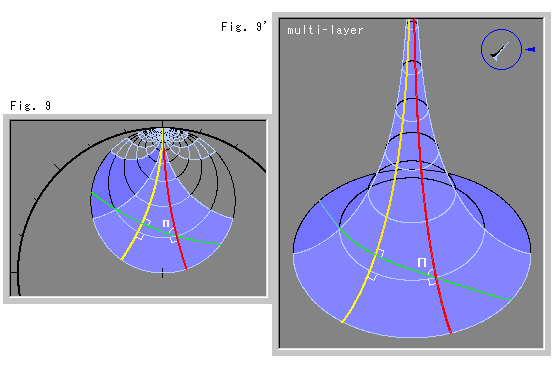
上のFig.9をご覧ください。
切り抜くところをホロサイクルの全体にして、多層擬球になるようにています。 しかし、見るところは着色してある一層だけです。 明るい色のところが、擬球の画面のこちら側になる方です。 赤と黄色の2直線は平行線で、緑色の直線が黄色い直線に垂直に引かれています。 緑色の直線の暗い色のところは、擬球の向こう側に延びているのを表現しています。
Fig.9'は、Fig.9に対応する擬球上の様子です。 右上の小さな図は傾けた擬球の側面で、青い矢印は見ている方向です。 赤と黄色の平行線が、まさしく無限遠で出会うのが見込まれます。 そして、平行角
も、ユークリッド空間内に埋め込まれている擬球上で正確に測れます。 輪切り線(円板上では同心円)が平行線である赤と黄色の両直線を垂直に横切っていますが、輪切り線は直線ではありません。
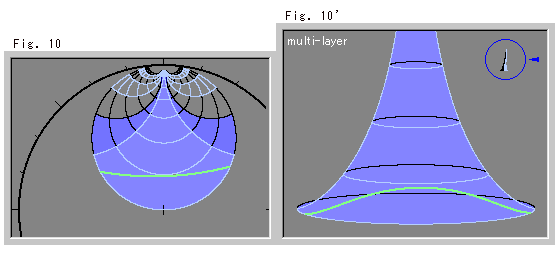
上のFig.10とFig.10'は、1本の直線をほぼ横に引いてみたものです。
下のFig.11とFig.11'は、斜めに直線を引いてみたものです。 Fig.11'では、直線が上の方へ登って行き、尻尾に巻きついて降りてきています。
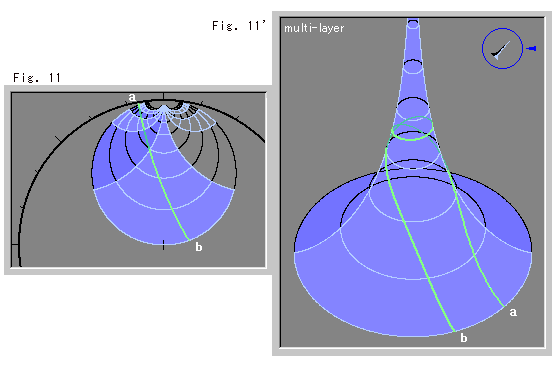
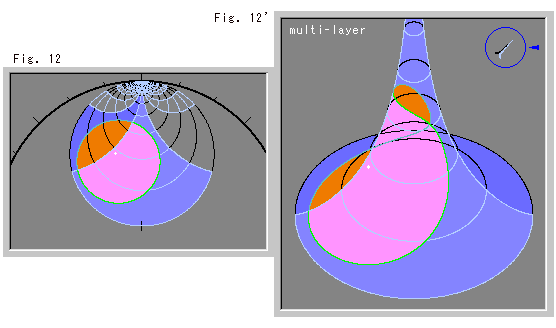
Fig.12は円です。 白い点は、その中心です。
Fig.12'は、それを擬球に写したものです。 はっきりと鞍形になっています。 この鞍形をそのままで平面とみなすだけで、ユークリッドの世界にいながら、その"平面"上で双曲幾何の成り立つのが、ふつうに測って見られます。
円の位置や大きさを少し変えると、Fig.13のように鞍形に重なったところができてきます。 重なるといっても、多層擬球ですから、擬球面の層を異にしています。
Fig.14は、もう少し円の位置と大きさを変えてみたものです。 鞍形は、多層擬球になんども巻きついて、尻尾の方へも広がっています。 わざと着色せずにおきました。
さて、双曲的平面は、ユークリッド空間で見れば、擬球でカバーできる範囲では、いたるところが鞍形になっていることが肯けました。 それでは、円板モデルの原点Oを含んだあたりは、どうなんでしょうか？ ごく狭い範囲でなら鞍形に似たものになっていると考えられます。
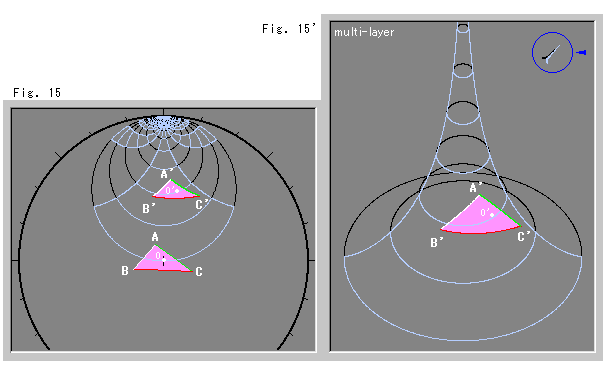
モデル円板の原点Oを内部に含む図形を擬球上に得ることはできません。 しかし、Fig.15のように三角形ABCをホロサイクルの上へA'B'C'として合同を保って移すことができます。 その新しい三角形A'B'C'なら、Fig.15'のように擬球上に描くことができます。 白い点O'は、三角形の内部にあった原点Oの位置をコピーしたものです。
擬球上で、このコピーした点O'を三角形A'B'C'に関する原点と捉えれば、原点Oを内部にもつ三角形ABCを擬球上に得たことになります。 むろん、真の原点Oが擬球上に写せたわけではありませんが、新しい三角形A'B'C'と新しい原点O'との関係は、もとの三角形ABCともとの原点Oとの関係と一致しています。 こうすることによって、ホロサイクル上にすっぽり移動できる図形なら、原点を含めたすべてのものを擬球上で見ることができます。
多層擬球をずるずるっと引きずり出したものは、ディニーの面(Dini's surface)とよばれています。 下のFig.16の絵は、それをノーズトランド氏が芸術的に描いたもので、 Gallery of Curved Surfaces から得ました。 なんと美しいではありませんか。 花びらのようですね。
擬球についてのWebに、la pseudosphereがあります。 説明はフランス語で、私も読めないのですけれど、絵を見つめることはできます。
ポアンカレの上半平面モデルから擬球を取り出すこともできますが、あとのCh.21で触れます。 歴史的には、円板モデルや上半平面モデルよりも、ベルトラミーの擬球が一番先だったそうです。