擬球がユークリッド空間での双曲平面であることを見ましたが、それは絵だけでした。 擬球を作っても、その上に実際に測地線を引いたり円を描くことは容易ではありません。 そこで、紙細工を工夫してみます。
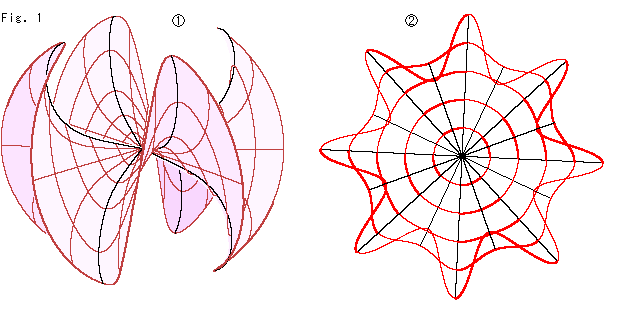
Fig.1をご覧ください。
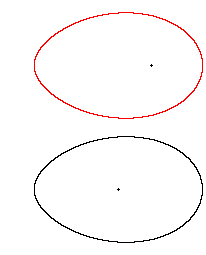
双曲平面をユークリッド空間で表現するのに、よく
のような鞍形が描かれています。 しかし、これは正しいでしようか？ 真上から透かして見ると、
のようになっています。 赤い曲線の太いところがこちら側（の上側）で、細いところが向こう側（の下側）です。
この図は精確な計算によったものではなく、観念的な作図です。 それにしても、なぜ、こんなにバランスよく整っているのでしようか。
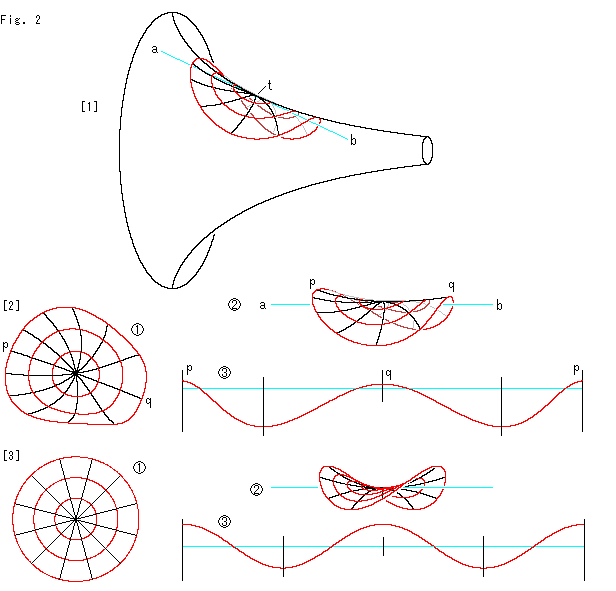
Fig.2をご覧ください。
[1]: 正確なのは擬球面です。 そこに円を描くと正しい鞍形が得られます。 水色の直線abは、鞍形の中心tを通る母線の接線です。
[2]: 鞍形をその中心tにおける擬球の法線方向から見ると、のようになっています。 は、接線abを水平にしたところです。 この鞍形の周をめぐって、その凹凸を見ると、
のように山と谷が不均一なっています。 pとqのところは山の高さが不揃いですが、2つの谷の深さは同じです。
[3]: 平凡な鞍形の一つです。 
として、a = 1/3 にとったものです。 曲率(Ch.24参照)は負ですが、むろん一定ではなく中心から離れれると急速にゼロに近づきます。 簡単のために、真上から見て円になるように切ってあります。 がそれです。 鞍形の中心の接平面を水平におくとのようになっていて、その周の浪打ぐあいはのように綺麗なサインカーブで均一です。 擬球面でできた鞍形と比べてください。
こうしてみると、擬球上の鞍形はいびつです。 それなのに、そのほうが精確だとはどうしてでしょうか？
紙細工をはじめます。 それぞれの図に工作用型紙へのリンクを添えてありますので、ご活用してください。
実際に工作しやすい大きさです。 百聞は一見にしかずといいますが、見ると触るは大違いです。 そして、さらに「百触れは一作にしかず」です。 紙細工をすることで、双曲世界の相当な実感を得ます。
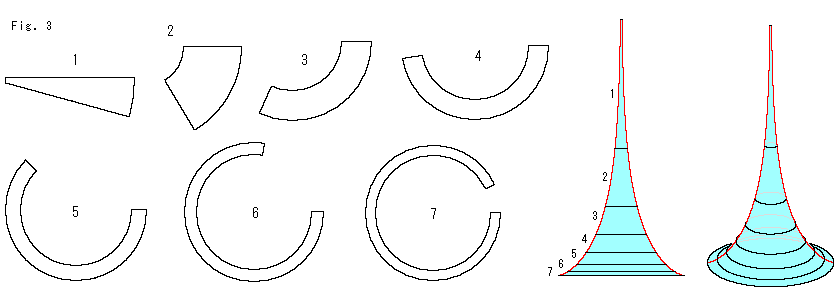[Fig.3の型紙]
上のFig.3をご覧ください。
擬球の紙細工です。 7つのアニュラス(環)です。 これらを円錐台形にして、順に糊で積み上げていくと、水色の擬球になります。 母線が折れ線になるので正確ではありませんが、実際に工作してみると、曲面の曲がり具合というものを会得するのにとても役立ちます。 数式を理解しているつもりでも、この紙細工で実感できることには及びません。
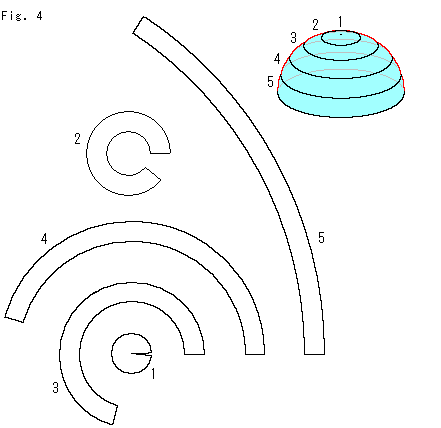
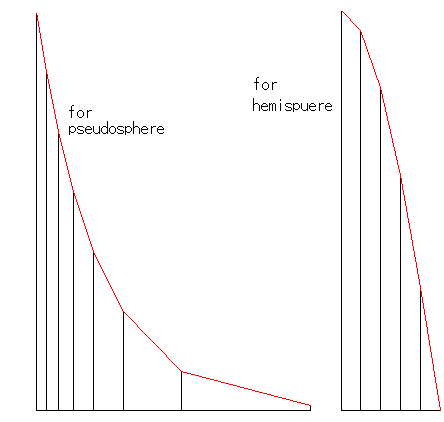
Fig.4をご覧ください。
比較のために半球をアニュラスでつくってみたものです。
右のグラフは、擬球(pseudosphere)と半球(hemisphere)のアニュラスを真っ直ぐにし、その長さを縦に巾を横にとったものです。 棒グラフになって隣あっている縦線は、各アニュラスの内側と外側の円弧の長さです。 棒グラフの先端をむすんだ赤い折れ線で見ると、当然ですが、傾きの変化がたがいに逆になっています。
[Fig.4の型紙]
上のFig.5をご覧ください。
いま作った擬球と半球を使ってみます。
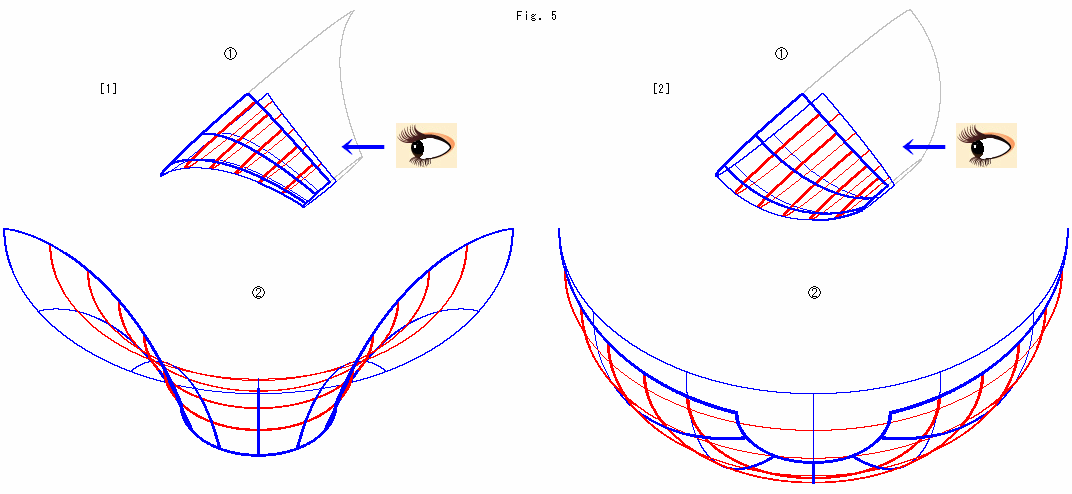
[1]: 擬球を軸で二分して、尻尾を適当に切り落として、のように覗きます。 すると、のようになっています。
[2]: 球面を中心を通る平面で二分して、極点付近を切り落として擬球と同様に傾け、のように覗きます。 すると、のようになっています。 球面を楕円幾何の平面として見立ててください。
目を近づけて眺めてください。 それぞれの視野には双曲平面と楕円平面の世界が広がっています。 両者の前方と後方の縁は、同じ大きさの半円です。
紙細工をつづけます。 擬球の鞍形は、ユークリッド的に見ると、四方に公平な曲がり方になっていません。 それで、例として
鞍形 
について見てみます。
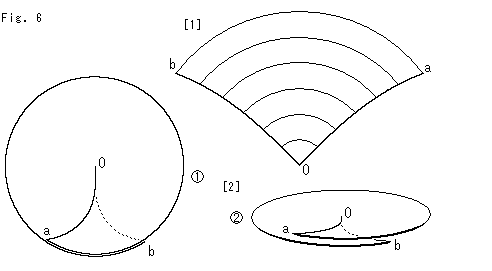
Fig.6をご覧ください。
[1]: このような扇形を4枚継なげばよさそうですが、aO,bOが大きく曲がっていて、頂点aとbが直角ではなく顕著な鋭角になっています。 これではなめらかな鞍形が得られません。
[2]: 点Oを中心とする回転方向に引き伸ばすことのできる材質のシートがあれば、図のように切りOaとObを継なぎ合わせるとできます。 でも、私たちにはそんな都合のよいものがありません。 やはり、紙を切っていくことにします。
鞍形がどのようなものかをよく見てみましよう。 この式は双曲放物面という曲面を表しているだけです。 鞍形そのものではありません。 鞍形とするには、たとえば上から見て円
といった条件をつけて、曲面から切り出しておく必要があります。
Fig.7をご覧ください。
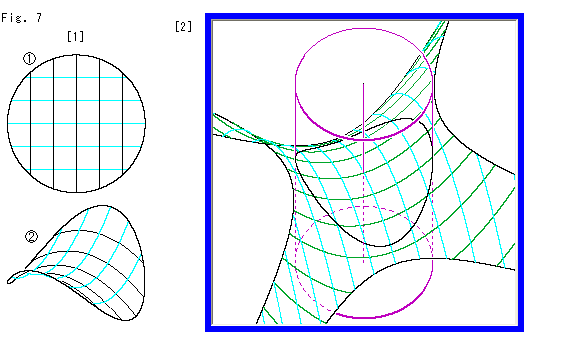
[1]: は、そのようにして得た鞍形に格子線を入れたところです。 r = 1 にとっています。向きを変えて見るとのようになっています。 格好よく見られる鞍形ですが、格子線は鞍形上を等間隔にとったものではありません。
[2]: この鞍形は双曲放物面を円筒でくり抜いたものです。 これでは曲面上の円、つまり中心から測地線の長さが一定距離の曲線とはいえません。
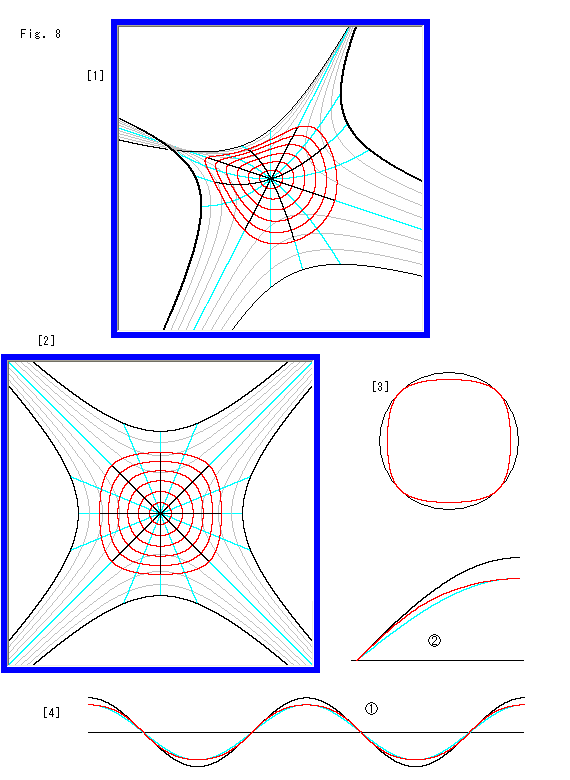
Fig.8をご覧ください。
擬球は回転面ですが、双曲放物面はそうではありません。 回転面に乗っていないものを回転軸に直交する平面で切ってアニュラスにするとことはできません。
[1]: そこで、双曲放物面上でその中心を中心とする同心円を描いてみました。 双曲放物面に沿って半径の長さを測り、その長さを一定に保った曲線からなるものです。 一番外側の双曲放物面上での半径をFig.7と同じ1にとっています。 描かれてある双曲放物面は、
の範囲です。
[2]: 真上から見たものです。
[3]: 赤い曲線の最外周をFig.7の円に重ねてみたところです。
[4]: は[3]の外縁を巡って見たところです。 黒い曲線は精確なサインカーブですが、赤い曲線はそうではありません。 水色の曲線は、比較のために赤い曲線と波の高さを一致させて描いた精確なサインカーブです。 赤い曲線はサインカーブではないのです。 部分拡大してみると、ようになっています。
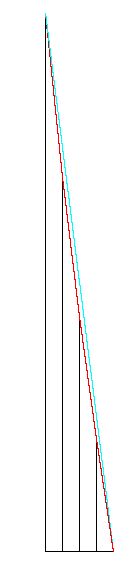
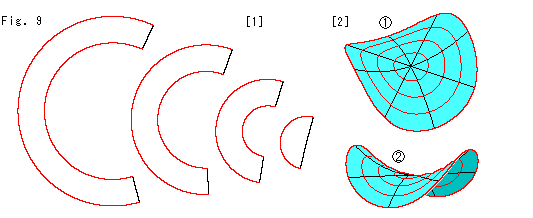
Fig.9をご覧ください。
上のFig.8の赤い同心円のアニュラスで鞍形を作ってみましよう。
[1]: 図のように切ったものを2組つくります。 同じ大きさのものどうしを継なぐと、4つのアニュラスができます。
[2]: アニュラスを順に継ないでできた鞍形です。 は上斜めから見たもので、はその向きを変えてみたものです。 [Fig.9の型紙]
右上の折れ線グラフは、Fig.4の右側にあるのと同じ意向のグラフです。 水色の線は赤い線の折れぐあいを見るために添えたものです。 赤い線が直線に近いのは、上のFig.8の[3]を見ればうなずけます。
Fig.10をご覧ください。
擬球全体に近いものを作るにはFig.3のようにすればよいわけですが、双曲幾何の世界を見るには、不便です。 擬球上の有限の領域を私たちの必要な範囲だとすると、都合のよいものができます。
[1]: 擬球が回転面であることに目をつけて、赤い双曲円のところをのように輪切りして、いくつかのアニュラスにします。 そして、糊で継ないでいくとのような鞍形を得ます。
[2]: この紙の鞍形を水平な面に置いて、定規で押さえつけて直線を引いているところです。 鞍形全体を平たく押さえつけることはできませんが、図のようなことをしても支障はありません。
[3]: 三角形を描いてから、押さえていた手を離したところです。 もとの鞍形に戻っています。 紙は、その面に垂直な方向には曲げやすいものですが、面はほとんど伸縮しません。 実際、紙を手にしてみると、まるでスプリングボードのようです。
[4]: できた三角形の各頂点にふつうの分度器を当てて内角を測っています。 小さめの分度器を使ってください。 それを鞍形に当てるときは、頂点付近だけを平たくします。
[5]: 見る向きを変えて、写真を鮮明な図になおしたものです。
[6]: 分度器で得られた内角の和は、180
ではなくて、合計(total) 37 + 43 + 90 = 170 です。 定規をつかい正確な直線を引いてつくった三角形がこうなっているのです。 これこそ双曲平面の世界です。 粗雑ですが、
測地線という難しい曲線が、ふつうの定規で引けたではありませんか！
[Fig.10の型紙]
ということは、定規でユークリッド平面に押さえつけられている直線状のところは、正しくユークリッド平面上です。 そして、もとの鞍形に戻るのは双曲平面へと移ることになるわけです。 このとき、辺の長さは保たれています。 しかし面積は、紙が伸縮しないので、ずっと双曲的なままです。
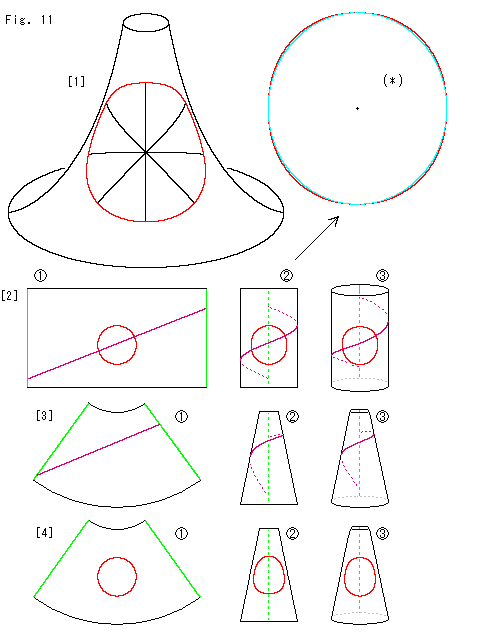
Fig.11をご覧ください。
擬球上の鞍形の形をよく見てみます。 それは大雑把にいって、円筒や円錐に似ています。 まず、それを見ます。
[1]: 擬球上に赤い円を描いたものです。 擬球は、円の中心で接する接平面が垂直になるように手前に傾けてあります。 黒い曲線は直径です。 よく見ると、S字形に見えています。 S字形の上の方は、下の方より大きく曲がっています。 Fig.10と同様に鞍形を定規で押さえてみれば、この直径は直線状になります。 赤い円は、下へ行くほど左右に広がって見えます。
[2]: 円筒と比べてみます。 はふつうの長方形に直線と円を描いたものです。 その長方形を巻いて円筒にします。 円筒をまっすぐに立てて見ると、のように見えます。 の直線が、円筒上ではS字形に見えます。 散髪屋の看板と同様です。 円筒もユークリッド面であって、S字形に見える曲線は測地線です。 赤い円は楕円になったように見えますが、精確には、そうではありません。 拡大してみると、図(*)のようになっています。 水色の曲線が正しい楕円で、赤い円はそれよりわずかにはみ出しています。 は、円筒を[1]と同様に傾けたものです。 傾けても、下の方が広がって見えることはありません。
[3]: 扇形から円錐台形にしたものです。 この場合も扇形上の直線が円錐上ではS字形に見えています。 [1]の直径も、これと同様です。
[4]: 円を[3]に描き込むと円錐にしたときに見にくくなるので、別に描きました。 では、赤い円の下の方が広がって見えています。 ところが、[1]と同様に傾けてのようにすると、その広がりは少なくなって見えます。
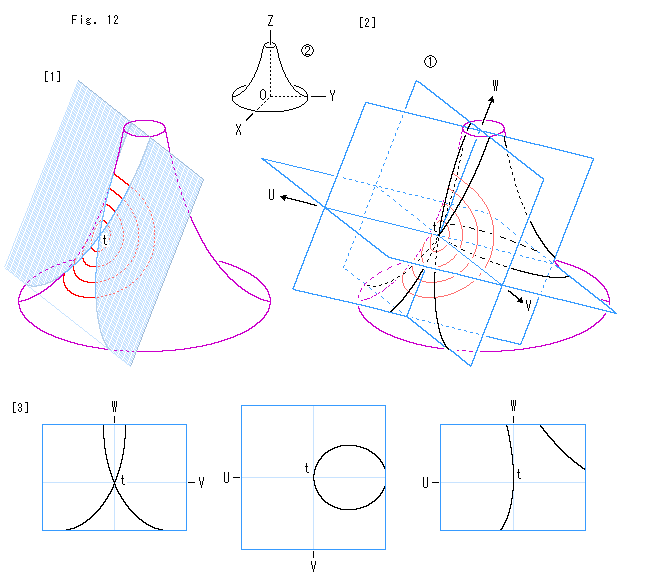
Fig.12をご覧ください。
擬球上の鞍形として同心円をとります。 それを取り出して都合よく見るために、擬球を3つの平面で切ります。
[1]: 同心円の中心tを接点とする接平面で擬球を切ったところです。
[2]: この平面に直交する2つの平面をのようにとります。 黒い曲線は各平面が擬球を切っている切り口です。 もとはのように座標軸をとってあったのですが、3つの平面に合わせて、鞍形の中心tを原点とする新しいUVW座標軸を定めます。 W軸は擬球の点tにおける接線そのものです。
[3]: 各平面の切り口を見やすいように平面ごとに並べたものです。 UV平面の切り口は楕円のように見えますが、そうではありません。
（接平面のことは、下の方のFig.22でまた取り上げています。）
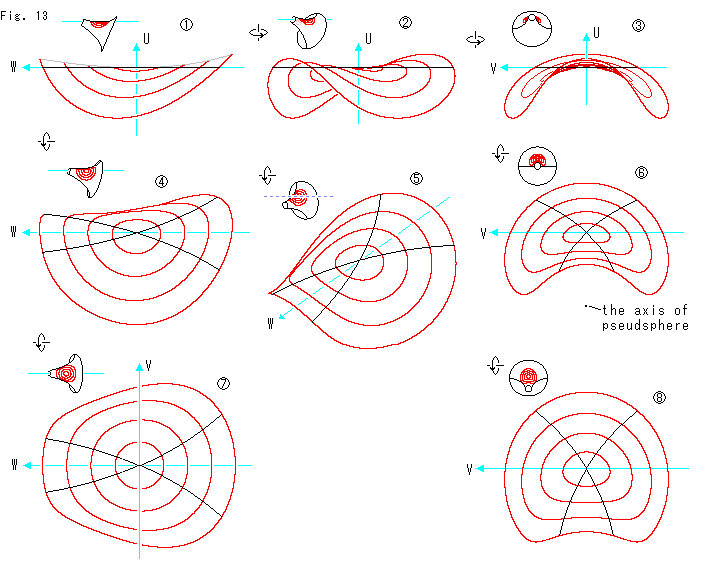
Fig.13をご覧ください。
同心円の鞍形をいろいろな向きから眺めてみます。 各図の小さな擬球は位置関係を見て取れるように添えたものです。 それに描かれている水色の横線は、接線(W軸)です。
大きな鞍形上の黒い線は、接平面(VW平面)で切られているところです。
,,は、VW平面を水平に保ってU軸を中心に黒い矢印のように45ずつ向きを変えたものです。
と
は、接線(W軸)を真横に保って、その接線を軸に45ずつ向きを変えたものです。
は、を傾けたものです。 画面に平行で鞍形の中心を通る直線（小さな擬球の点線(W軸ではありません)）を軸にして、黒い矢印の方向に45回転しています。
は、V軸を真横に保ちながら擬球の軸(Z軸)が画面にちょうど垂直になるように傾けたところです。 黒いスポットが擬球の軸(the axis of pseudosphere)です。
は、から45傾けたものです。
鞍形をいろいろな方向から見るには、紙細工した鞍形を手にすれば済むことですが。 それは実感を得るにはベストですけれども、精確に見るにはこのような作図が必要です。
これで擬球の鞍形がどう歪なのかがわかりました。 同心円を大きくすれば、もっと歪になってきます。
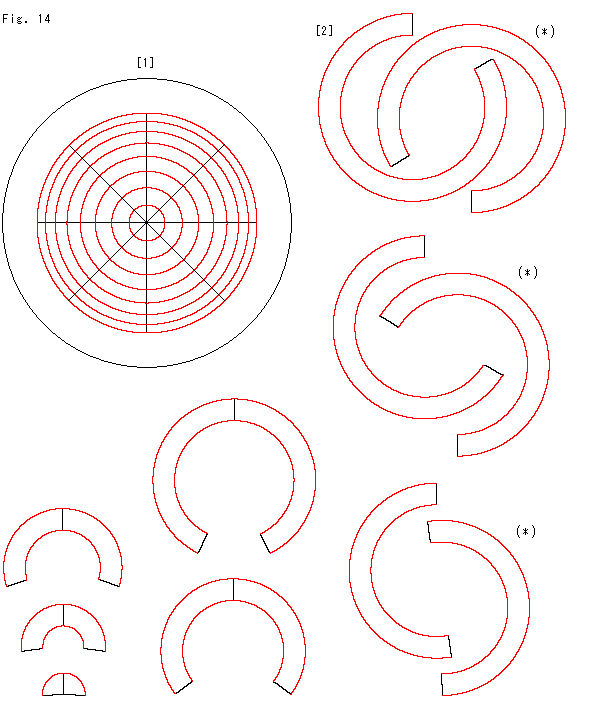
Fig.14をご覧ください。
平坦なモデルであるポアンカレ円板から鞍形を作ってみます。 そうすれば、歪んでなくて縁が公平に波打っている鞍形を得ることができるはずです。
[1]: ポアンカレ円板です。 双曲同心円の中心はどこにとっても同じですが、円板の中心に合わせておくと見やすいので、そうしておきます。
[2]: (*)印のアニュラスは、2つを継ぐと180分になります。 (*)印のないアニュラスは、それぞれで180分になっています。 同じ形の180分のアニュラスを2つ継ないで360分にしたものを貼り積んでいくのです。
アニュラスの形は四方に同じものですから、縁が公平に波打った鞍形になるに違いありません。
[Fig.14の型紙]
Fig.15をご覧ください。
上のアニュラスで作った紙細工です。
[1]: 中心付近だけをとって作ったものです。 のように真上から見ると、公平に波打った鞍形になっています。
[2]: ところが、中心からもう少し離れたところまでのものを作ると、写真のように大きく波打って、山と谷の数も増えてきます。 部分ぶぶんは鞍形ですが、全体を鞍形と呼ぶにはふさわしくありませんね。 ヒラヒラと仮称しておきましよう。 このヒラヒラは作図で描こうにも容易ではありません。 もっと広い範囲のものを作ろうとすると、山や谷が中心の方へと塑り返って、面と面が突き当たってしまいます。
はじめのFig.1と見比べてください。
しかし、どんなにヒラヒラになっていても、上のFig.10と同様な実験をしてみることで、双曲世界を鑑賞することができるはずです。“はず”といったのは、図形が双曲的なものになることは間違いないのですが、できた鞍形の形が擬球から作ったものとは違うからです。 よく見ていきましよう。
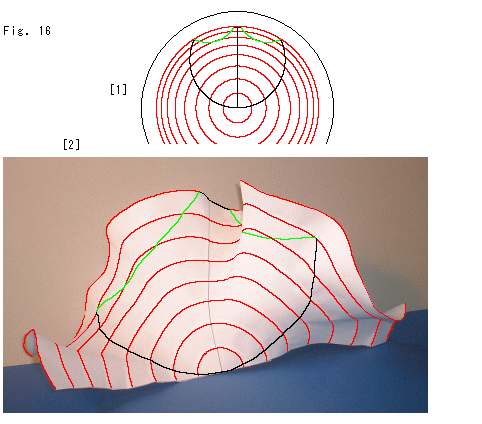
Fig.16をご覧ください。
ポアンカレ円板から擬球に対応するところを切り出して、アニュラスにきざんで擬球を作ってみます。
[1]: 円板内の黒と緑の曲線で囲んだところが擬球との対応部分です。 緑色の曲線と中央の縦線が擬球の母線に対応しています。 小さな黒い曲線は擬球の尻尾を切り落とした切り口で、大きい黒い円弧は擬球の開口部に当たります。
[2]: ヒラヒラでは、こうなっています。（不要な下半分は省いています。）
[3]: 擬球にするためのアニュラスです。 これは、平坦なポアンカレ円板から取り出したものです。 赤い同心円に沿って切り出したものですが、緑色の母線になるところが小片に分かれているので、ちょっと工作がやりくいです。
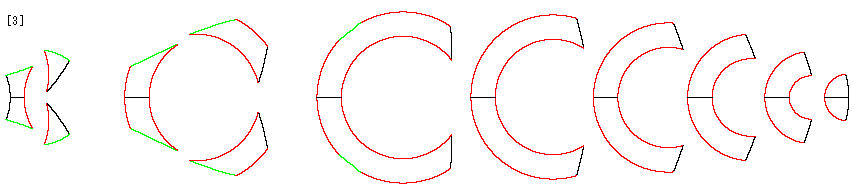
下のFig.17をご覧ください。
工作しやすいように擬球の輪切り線に合わせてポアンカレ円板から取り出したアニュラスです。
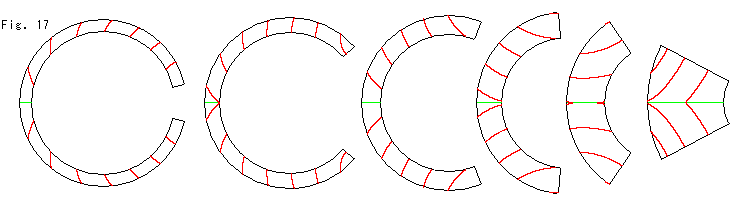[Fig.16,17の型紙]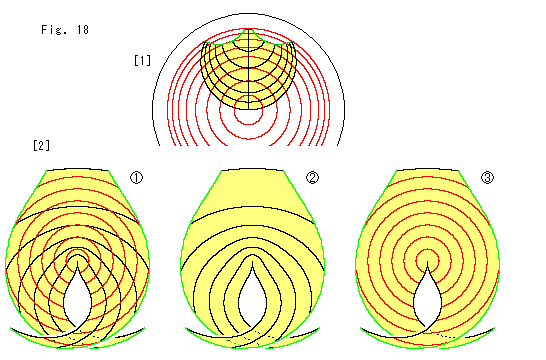
Fig.18をご覧ください。
[1]: ポアンカレ円板上の赤い同心円に擬球の輪切り線の対応曲線を重ねて描いたものです。 黄色いところが擬球と対応しています。 Fig.15のアニュラスは、この黒い曲線に沿って取り出しています。 擬球の対応領域では、赤と黒の曲線が上下逆に曲がっています。 それにもかかわらず、Fig.16とFig.17のいずれのアニュラスからも同じ結果が得られます。 どうしてでしようか？
[2]: 擬球に対応する領域を、原点を中心とする円周方向と半径方向が双曲的長さにすると、のようになります。 図の長さスケールは[1]の1/4倍に縮小しています。 とは、を輪切り線と同心円のそれにわけて描いたものです。 Fig.16とFig.17のアニュラスはこれに拠って作ったものです。 つまり、ポアンカレ円板上の各点の場所を双曲長で捉えているのです。 これが、Fig.16とFig.17でアニュラスの形はちがっていても同じ擬球になるわけです。
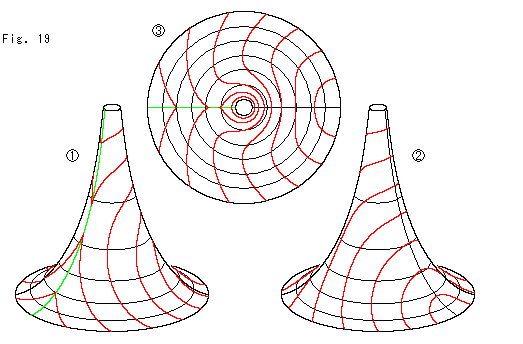
Fig.19をご覧ください。
上のFig.17のアニュラスで作った擬球です。 Fig.16の[3]のアニュラスで作れば、擬球の輪切り線が出ないだけです。 赤い曲線がポアンカレ円板上の同心円です。
は、緑色の母線が見えるように置いたものです。
は、その反対側の黒い母線が見えるように置いたものです。
は、擬球を真上から見たところです。
興に乗って遊んでみましょう。
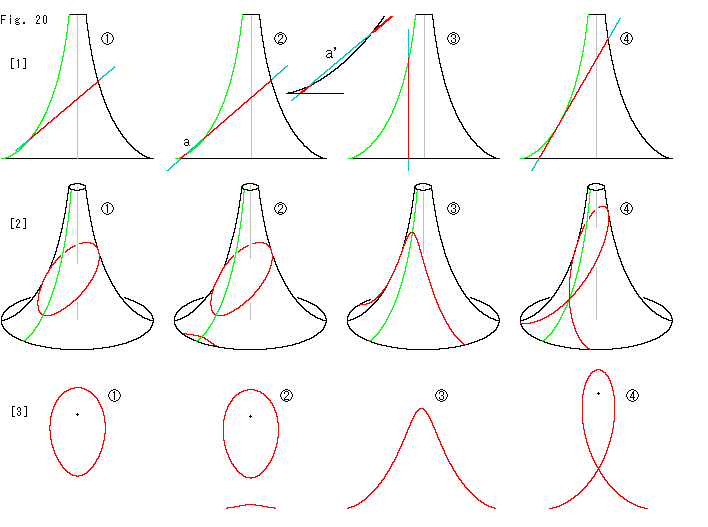
Fig.20をご覧ください。
擬球を平面で切ります。 灰色の線が擬球の軸で、赤い線が平面による擬球の切り口です。 切り口の形は、平面の傾きや擬球の軸を切る位置によって変わってきます。
[1]: 直立した擬球を、平面が画面に垂直なるようにして見たものです。 赤い切り口をはさむ母線の一方を緑色にしています。
は、母線が切り口の縁を完全に挟むように切ったものです。
は、平面の傾き(迎角)を少し大きくした場合です。 平面が途中で擬球から離れ、擬球の裾も少し切っています。 その付近aを拡大してみると、図a'のようになっています。
は、平面を擬球の軸と平行にしたところです。
は、接平面で切ったものです。
[2]: 擬球からはみ出している平面の部分を除いて、切り口を残してを斜めから見たものです。
[3]: 切り口だけを取り出して、真正面に並べてものです。 黒いスポットは擬球の軸が貫通している点です。
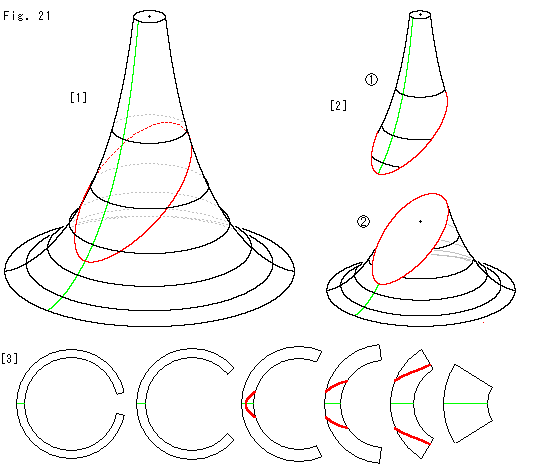
Fig.21をご覧ください。
上のFig.20の一番左側の列の場合をとります。
[1]: 紙細工のための輪切り線をいれています。
[2]: 平面で切った擬球を実際に2つに分離したところです。
[3]: [1]のアニュラスです。 はじめから[2]のようなものを作ることも、勿論できます。 しかし、まず[1]を作って、それを2つに切り離すほうが面白い。 しかも、簡単です。 [Fig.21の型紙]
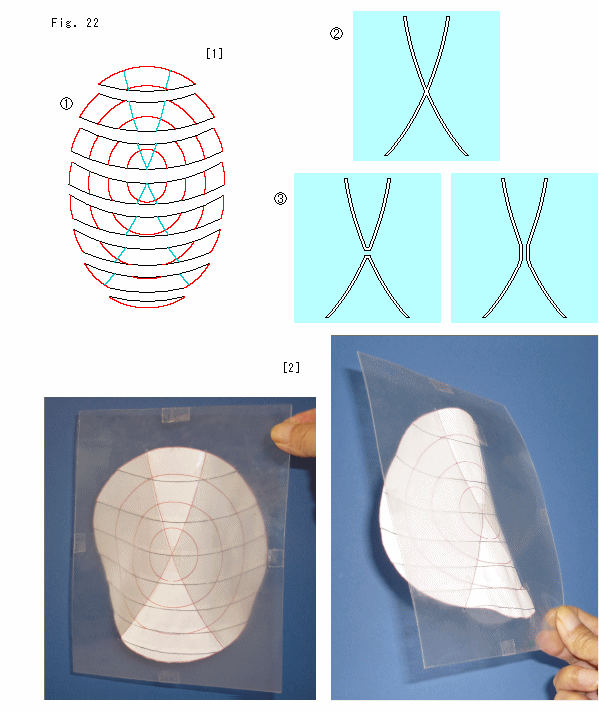
右下のFig.22をご覧ください。
接平面で切るFig.20の一番右の列については、Fig.13の鞍形で見てみます。
[1]: は鞍形を作るアニュラスです。 緑色の曲線が接平面が通っているところです。 は、この鞍形と接平面との関わりを見るためのものです。 透かして見れるシートをＸ字形の溝にくり抜きます。 のような中央部の左右か上下が細く続いたものでもかまいません。 この溝へ出来た鞍形を差込みます。
[2]: すると、写真のようになります。 接平面のシートは[1]のの2枚を重ねてつかっています。 シートはプラスチックです。 きっちりした平面ではありませんが、状態はよくつかめます。 むろん、鞍形のほうを切って、それでシートを挟んでもかまいません。（写真の鞍形の接平面との共有曲線は赤色です。） [Fig.22の型紙]
ところで、Fig.21のように擬球を切った断面は楕円ではありません。 いわゆる卵形です。 それでは、どのような卵形になっているのでしょうか。
円錐は裾が広がっているので、それを斜めに切った断面は卵形になる気がします。 しかし実際には、よく知られているように楕円になります。 それなら、円錐よりも裾が広がっていく擬球のようなものを切れば、卵形が得られるはずです。 まず、円錐と円筒を見てみます。
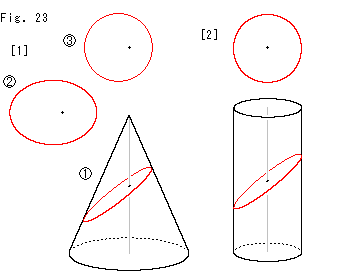
Fig.23をご覧ください。
[1]: 円錐をのように切って断面を正面に向けると、の楕円になっています。 真上から円錐の軸方向に見ると、のようになっていて、円です。 黒いスポットは、見下ろしたときの円錐の軸で、円の中心ではありません。
[2]: 楕円の短径を半径とする円筒を[1]と同じ傾きの平面で切ると、まったく同じ楕円が得られます。 それを真上から見ると円になり、円筒の軸と円の中心が一致します。
ここで気付くことがあります。 円錐の頂点を上の方へ限りなく伸ばしていけば、円筒になるはずです。 つまり、円筒は頂点の高さが無限大の円錐だと考えられます。
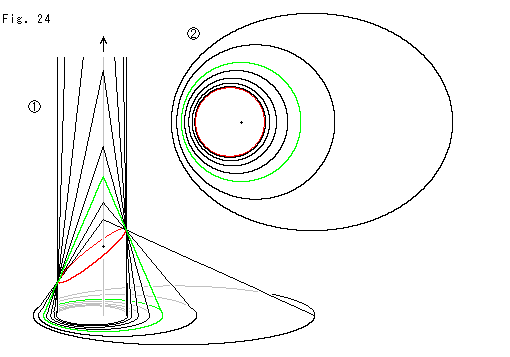
Fig.24をご覧ください。
水平に固定したテーブル上にFig.23の円錐を立てます。 円錐と赤い楕円を接触させたままで、円錐の頂点を下から上へとのように真っ直ぐに引っ張ります。 緑色のがFig.23の円錐です。 頂点がそれより低い円錐の底面上から見ると、で見るように楕円になっています。 頂点が緑色の円錐より上へ越えていくと、底面の形は円のままで、楕円の俯瞰と重なろうとします。 極限においては、重なって一致するに違いありません。 そのとき頂点は何処へ行ったのかと問われると困るのですが、にはユークリッド的にその位置を黒いスポットで表しています。
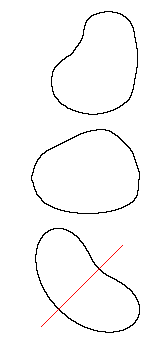
それでは、卵形に取り組んでみましよう。
卵形曲線には明確な定義がありません。 数学書を見ると、「閉曲線であって、内部の任意の2点をむすぶ線分がその閉曲線を切らないもの。 凸閉曲線ともいう。」と書かれています。 つまり、凹んでいないループならどんなものでもよいのです。 むろん、卵形とよぶからには、なめらかな曲線でなければなりません。 そして、ここでの卵形曲線はニワトリの玉子のようなものを指すことにします。 すると、2次曲線には対称軸が2本以上ありますが、私たちの卵形曲線では1本の対称軸が必要で1本にかぎられることになります。 右図のような窪みがあったり、非対称なものはダメです。 対称軸が1本あっても凹んでいるのはいけません。
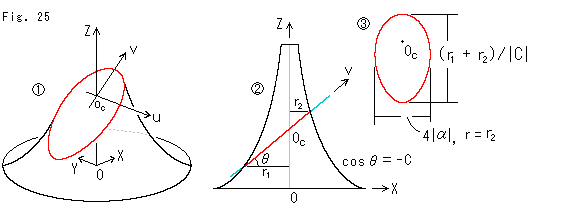
Fig.25をご覧ください。
これは、Fig.21のものです。
: 擬球はXYZ座標で描かれていますが、赤い卵形を見るために、擬球を切断した平面上に新しく2次元のUV座標系をとります。 UV座標系の原点OcはZ軸上にあります。 XZ平面とVZ平面は重なっており、YZ平面とUZ平面が重なっています。
: 平面を画面に垂直にしたところです。 平面
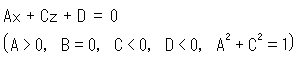
に拠って
, 
, 
が定まります。
: 卵形を真正面においたところです。 卵形のふくらみは、擬球の半径rが小さくなっていく上の方で逆に大きくなっています。 擬球は裾の方が広がっているのだから、下側で膨らんだ卵形になると思ったのに、そうはなりませんでした。 どうしてでしょうか。
私たちの卵形曲線の計算は、擬球の半径rをパラメータとして
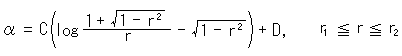
と略記したものを用いて、
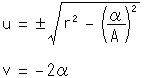
としたものです。
しかし、こんな式を見ただけでは、どんな卵形か直ぐにはわかりません。 そこで、卵形は楕円を変形すればよいと考えて
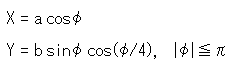
と式を立てました。 そして a = 0.58, b = 0.392 にすると、右図のように視覚的にぴったり重なる卵形ができました。 赤い卵形は擬球の半径rをパラメータに使ったもので、横にねかせています。 黒い卵形が上式によったものです。 それぞれの黒いスポットは原点で、これだけが違っています。
でも、どうも、まぐれ当たりのようですね。 平面の傾きを変えると、この手はたちまち崩れてしまいます。 とはいえ、擬球を平面で切るということに関しては、双曲幾何と何らかのものがあるような気がしなくもありません。
卵形については、インターネットのTDCCLAB.SATELITE やEgg Curves にいろいろな式が出ています。
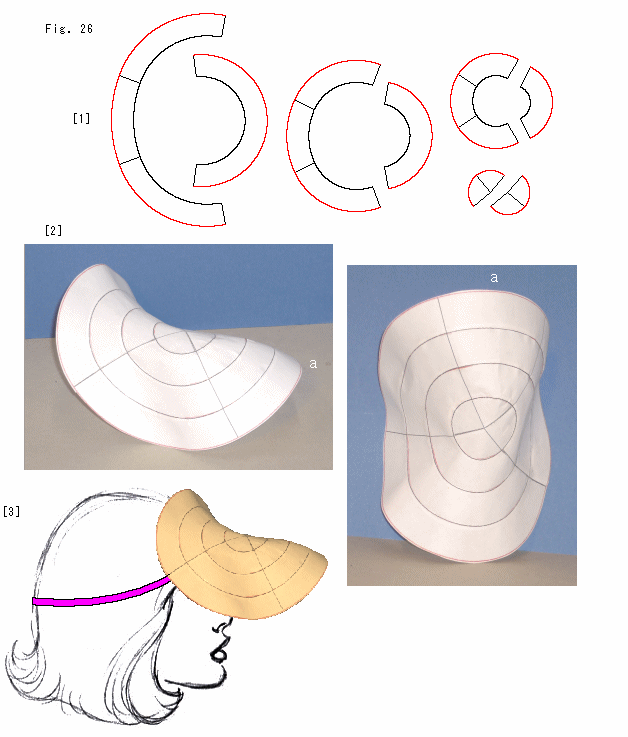
Fig.26をご覧ください。
狂った紙細工です。
[1]: このアニュラスから何が作られると思いますか。 実は、計算をまちがったシロモノです。
[2]: そうとは気づかずに、紙細工をしたものです。 出来上がってみると、なんと双曲的な曲面と楕円的な曲面がなめらかに継ながっているではありませんか！ aは、曲面の向きがわかるように付けた印しです。
曲面を表す数式としては、右図のような上が擬球の部分で下が球になったもので考えればよいでしよう。
[3]: たわむれに、インターネットに住む彼女の日よけ帽子にしてみました。
[Fig.26の型紙]
こんなものができたので、曲率を異にする曲面を擬球に継なぐことを意図的やってみましょう。 それができれば、ユークリッド空間内に居ながらにして、双曲的世界や楕円的世界へ移ることができます。 むろん無事生還できます。
右のFig.27をご覧ください。
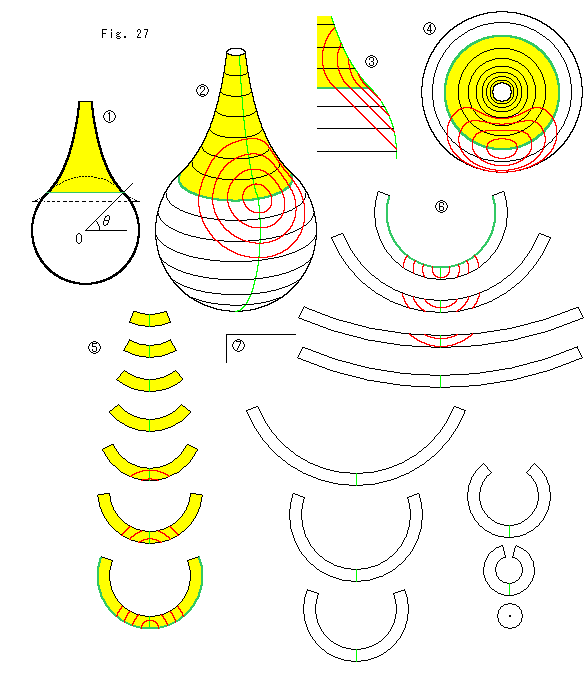
: 黄色い擬球の裾を切って単位球Oに接続させます。 緑色の線がその境界です。 単位球を用いると、境界線は球Oの緯度がちょうど45になるところにきます。 そして、球Oと擬球はなめらかに継ながります。
: アニュラスで作った完成品です。 黒い線はアニュラスの継ぎ目です。 その間隔は、擬球上も球O上も同じです。 縦の緑色の線は、様子がわかるようにと描き入れたもので、工作の便にも役立ちます。 赤い曲線は、境界線上に中心をおいた同心円です。 同心円の各円は等間隔です。 その間隔は、擬球上では擬球の測地線に、球O上では球の測地線に沿って長さを測っています。 同心円も境界線でなめらかに継ながっています。
: 真っ直ぐに立てて、すこし拡大して真横から同心円の付近見たものです。 球O上では直線状になって見えます。 しかし、擬球上の同心円とはなめらかに継ながっています。
: 真上から見たものです。
: 裾を切った擬球部分のアニュラスです。
: 球Oの擬球との境界から赤道までのアニュラスです。 そこに同心円の下半分が入っています。
: 球Oの赤道から下のアニュラスです。
[Fig.27の型紙]
さて、曲率が-1である擬球と+1である球面を継ないだ滑らかな(?)曲面が得られました。 しかし、曲率が -1 から突然 +1 に変わっているのに、その境界で曲面がなめらとは、なにかしら奇妙に感じられます。 なによりも「滑らか」の定義をちゃんと知らねばなりません。
面ではない平面曲線の場合でも、異なる曲率のものを日常的な意味での滑らかさで継なぐことは簡単にできます。 いままで、気にしたことはなかったのですが、ものの曲がり具合をもっと巧く表す方法があるのではないでしょうか？
それを考えるのはちょっと後にして、他の例を見てみましよう。 何かヒントが得られるかも知れません。 しばらく「滑らか」ということばを日常的な意味でつかいます。
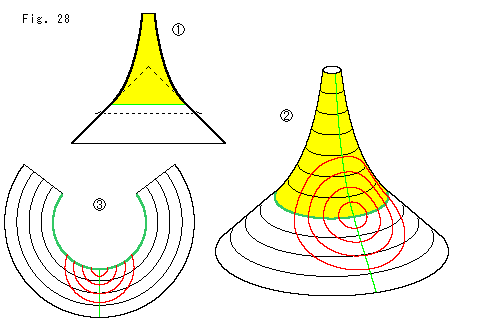
Fig.28をご覧ください。
: 擬球の裾を切ってに円錐に接続させます。 境界線はFig.27と同じです。 同心円がなめらかに継ながっています。
: アニュラスで作った完成品です。
: 境界線から下の円錐のアニュラスです。 1枚の紙です。 その上の同心円は当然、ふつうの同心円と変わりありません。 擬球部分のアニュラスはFig.27のと同じです。 [Fig.28の型紙]
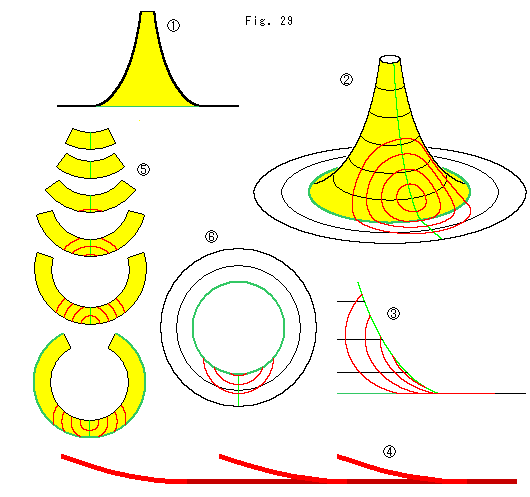
Fig.29をご覧ください。
: こんどは擬球の裾を切り捨てません。 そして、その縁に平面を接続します。 平面は高さゼロの円錐ともいえますね。
: アニュラスで作った完成品です。 同心円が折れているようにも見えますが、そうではありません。
: 真っ直ぐに立てて真横から見ると、あれっ？ やはり折れているのかな。
: もうすこし拡大して、平面へ移ったところを色濃くしてみました。 そしてよく見ると、同心円の各円がなめらかに平面の方へと伸びているのが、はっきりとわかります。
: 擬球部分のアニュラスです。
: 平面部分のアニュラスです。 1枚でできています。
[Fig.29の型紙]
こうして、曲率が-1である擬球から曲率が+1や0の曲面へなめらかに移ることができるのを手と目で確かめました。
つぎは、曲率が-1から連続的に変化する曲面を擬球に継なぐことを考えます。
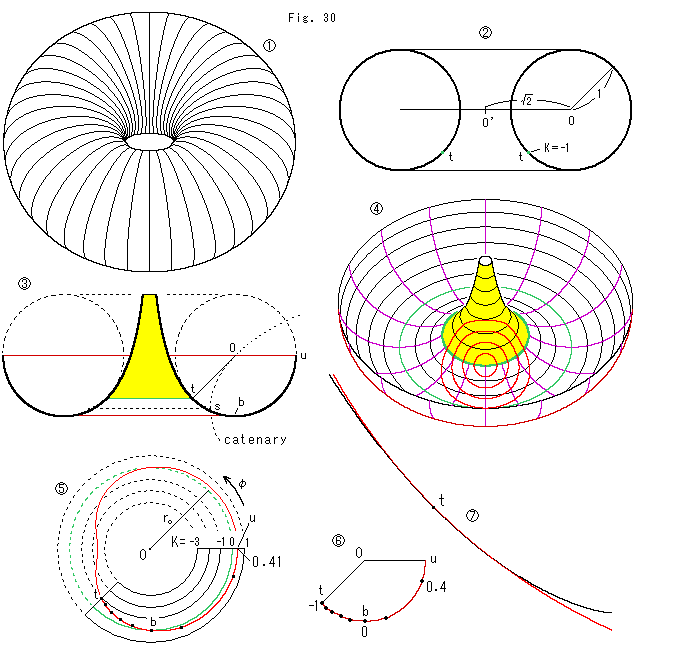
Fig.30をご覧ください。
: トーラスは、その上をどう移動しても曲率の変化は連続的で、正にも負にもなります。 これを利用してみます。 トーラスの輪の内側の面は曲率が負ですから、擬球をその内側で接するようにします。 接するところは、Fig.27で球と接続していた同じところ（ = 45）を選びます。 よく肥えたトーラスになりました。
: トーラスの断面です。 擬球との接点tでトーラスの曲率Kが-1になるようにしてあります。 このとき、トーラのスチューブの半径はちょうど1で、輪の半径OO'は
になっています。
: このトーラスを擬球に嵌めたときの断面です。 点sは擬球の切り捨てた裾の先端（もとの擬球の開口部の縁）です。 点bは天底です。 利用するトーラスは、チューブのt-b-uの範囲です。 点線のカーブは、チューブの中心と点sを通っているカテナリー(catenary)とよばれている曲線です。 擬球の外側に接する円の中心は、円がどこにあってもこのカテナリー上にあります。
: アニュラスで作った完成品です。 ずいぶん広がっています。 トーラスの外周の半径は、擬球との境界線の半径の 2+ 倍になっています。
: トーラスの曲率Kの変化を極座標r
で表したものです。 実線のところが私たちのトーラスの部分です。 適当なところに K=0 の動径
をとって、緑色で描いています。 黒いスポットは点tから曲率Kを0.2ずつの間隔できざんだところです。 チューブを1周すると曲率Kは
の範囲で変化します。 曲率Kが+1になるところはありません。
: トーラスのチューブの断面で曲率Kの様子を見たものです。
: 断面では擬球の切り捨てた裾とトーラスがかなりの範囲で重なっているように見えます。 どうなっているのか、接点tの近くを10倍に拡大してみました。 黒い曲線が擬球で、赤い曲線がトーラスです。 トーラスは接点tから上の方もあるとして描いてあります。
これで、曲率もなめらかに変化する曲面を擬球に継なぐことができました。 [Fig.30の型紙]
トーラス上へ延びている同心円は、トーラス上の測地線に沿った距離で半径をとり描いたものです。 しかし実は、その測地線の形状は推測で定めたのです。 証明は私どもには未だできていないのですが、どう考えたかを示しておきます。
トーラスの面積と体積は、そのチューブと同じ半径rと中心線の長さ
をもった円筒と同じです。
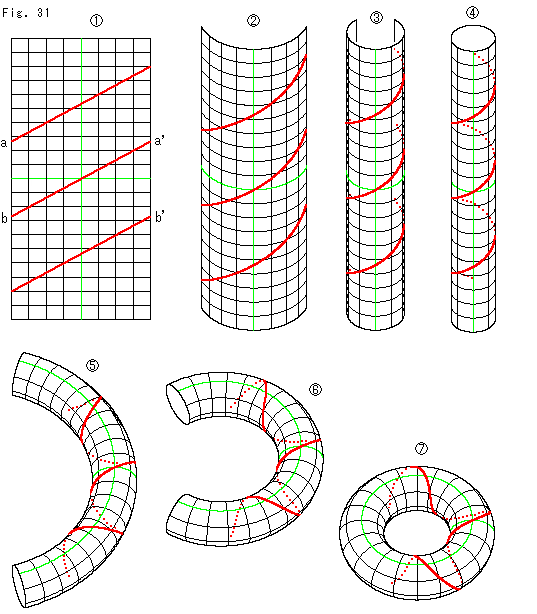
Fig.31をご覧ください。
平坦な短冊にのように平行な直線を引きます。 a,a'とb,b'はそれぞれ同じ高さです。 その短冊を,のように巻いて円筒にします。 そして、,のように曲げていき、両端を継なぐとトーラス
になります。 トーラスに巻きついた螺旋ができています。
始めに短冊上の赤い直線を伸び縮みしないでよく滑る紐に代えておくと、トーラス上の螺旋はどうなるでしょうか。 螺旋が測地線だといおうとするのですから、その長さを測っておかねばなりません。
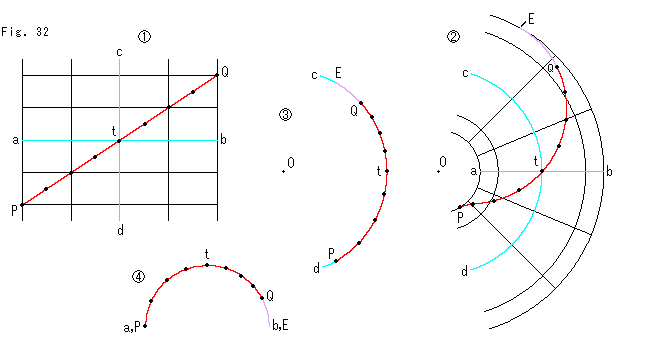
Fig.32をご覧ください。
: 短冊上の直線(紐)です。 トーラスにしたときに上から見える範囲だけを描いてあります。 点Oはトーラスの中心です。
: その中点tだけを固定しておいてトーラスにしたものを真上から見たところです。 黒いスポット間の距離はと同じです。 端点Qがトーラスの外縁Eまで行かずに途中で止まっています。 もう一つの端点Pも内縁から少しはずれているはずですが、図ではしかと見えません。
: トーラス上の赤い曲線を真上から見たままで、円弧cd上へ点Oを中心とする中心射影したものです。 中心Oからトーラス上の赤い曲線を眺めると、パノラマ風にこうなっているわけです。
: トーラスを水平にして螺旋の高低を見たものです。 螺旋を半円a-t-b上へ回転射影したものです。 ,とあわせて螺旋の形状を見て取ってください。
このことからわかるように、上のFig.31に描かれている螺旋上の各点は、円筒を曲げて行くときも円筒上の対応点に終始固定されていたのです。 つまり、トーラス上の螺旋はもとの円筒上の螺旋が引き伸ばされたものです。
トーラスに擬球を継いだFig.30の同心円は、こんな引き伸ばしのない長さで測地線上を測って描きました。
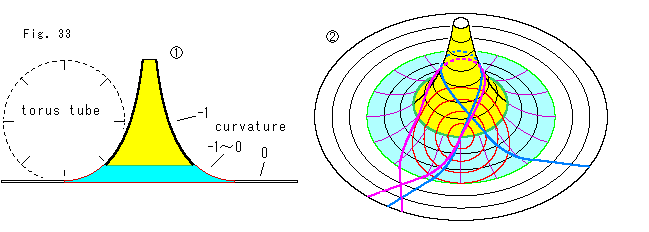
Fig.33をご覧ください。
もう一つだけ描いてみます。
: 擬球と平面の間にト―ラスのチューブ(torus tube)の1/8を置きます。 水色のところが、そのト―ラスの部分です。 すると、曲率は-1からゆるやかに0となり、曲率0の平面に移ることができます。
: アニュラスで作った完成品です。 同心円がト―ラスのところでとどまっているので、ピンクと青の2本の直線を太く引きました。 それぞれの直線は各面の測地線を這っているので、平面上から出発した直線は、擬球をぐるりと回ってもとの平面に戻っています。 ピンク色のコースなら、平面上の出発点へ戻れます。 別世界へ行ったからですね。
出発点へ戻れるというと、楕円幾何の球面モデルを思い出します。 しかし、ここには球面はまったくありません。 平面から擬球を眺めると、擬球という山があって、直線は最短登山コースだとも空想できます。
青い直線が擬球上で自分自身と交差しているように見えますが、そうではなくて、擬球の面がロール状に多層なっているのだと想ってください。 [Fig.33の型紙]
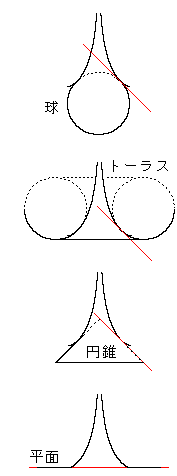
「滑らか」とはどういうことでしようか。 国語辞典を開くと、面に角張ったところがなくザラザラしていないことだと書いてあります。 数学の本では、
級の曲面（xとyで1回偏微分できる曲面）なら滑らかな曲面だと書いてあるのもあり、
級の曲面（xとyで2回偏微分できる曲面）なら滑らかな曲面だと書いてあるのもあります。 また、滑らかな曲面というからには、無限回微分できる
級のものでなければならないという数学者もいます。 私たちは、無限回微分できるものこそ精確無比だと感じます。
しかし、右図のように2つの曲面が接平面を共有するということだけで紙細工をしてきました。 そして、滑らかに見えます。 つまり最低限、級のものであれば足りると思えます。
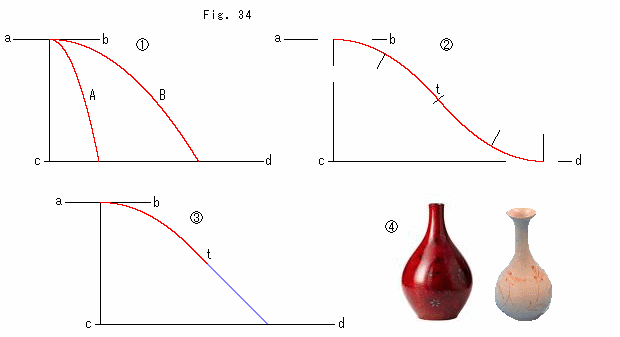
詳しく見てみましょう。 Fig.34をご覧ください。
平面曲線で見てみます。
: 水平な2直線 ab, cd を放物線でむすんだものです。 放物線AとBはどちらも上端の接線は直線abと一致しています。 しかし、放物線Aよりも放物線Bの方が「なだらか」です。 それはAの曲率がBの曲率より大きいからです。「なだらか」という用語は数学では、なぜか使われていません。
: なだらかな方の曲線Bをとって、その真ん中tから下を逆向きの放物線で継ないだものです。 このS字形の曲線に法線を立て、その長さを曲率にしています。 法線の向きは曲率円の中心方向です。 中点tでは右上へと左下への2本が立っています。 曲率ゼロではありません。 曲線をたどって点tを通るその瞬間、曲率の正負が代わります。 でも、そこはなだらかではありませんか。
: 点tでの曲線の傾きでもって、そこから下を直線にしてみたものです。 下端を除けば、どこも角張ってはいませんが。 けれども、なにかしらシャープな感じがしませんか。
: 花瓶です。 どれも滑らかで、なだらかではありませんか。 その母線(平面曲線)との曲線を見比べてください。
こう見てくると、どうも人間は、曲がっているものはずっと曲がっていてほしい。 そして、曲がる方向が逆になっても、なだらかであればよいという性癖をもっているのではないでしょうか。
それにしても、2つの放物線を継ないだものは、その継ぎ目では接線を共有していますが、そこでの微分には疑問がありますし、数学的には滑らかとはいえません。 しかし、なぜ滑らかに見えるのでしょうか。
異なる2つの曲線を継ないで1つの曲線にしたとき、それを1つの式で表すことができれば、継ぎ目で滑らかかどうかを明確にいえます。 でも、そんな1つの式を見出すことは容易ではありません。 無理な気もします。
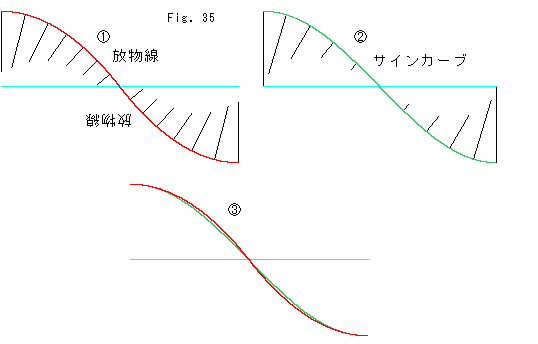
Fig.35をご覧ください。
: 放物線を逆さに継いだものに曲率の大きさにあわせた法線を並べたものです。 法線を立てておくと曲がり具合の程度がよくわかります。
: ふつうのサインカーブです。 サインカーブは、無限回微分できるので完全に滑らかです。
: サインカーブに赤いの曲線を重ねてみたところです。 かなり近似して見えますね。 この真に滑らかなものとよく似ていることから、私たちは継ぎ目をもつ曲線も滑らかであると認識するわけです。 そして、実用上なんら支障はありません。 ただし、継ぎ目のある曲線が「なだらか」であることが必要です。
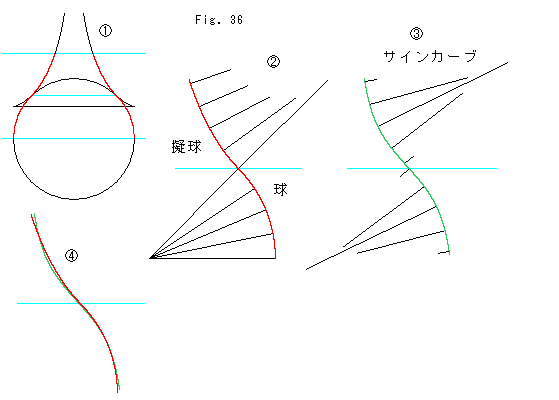
Fig.36をご覧ください。
上の考えにならって、擬球との関係を見てみます。 曲面としてでなく、平面曲線である母線をとって調べます。 私たちの考えている曲面はいずれも回転面ですから、それでたります。
: 擬球と球面を連結してなる曲面の母線です。 赤く染めた範囲の母線の近似曲線をつくります。 下側は球の赤道まで、上側はそれと同じ高さまでです。 中間の水色の線は接点を通っています。
: 擬球の曲率を表している法線は、平面曲線である母線のものです。 曲面の曲率は、むろん一定の -1 です。
: 基線を斜めにしたサインカーブです。 曲線の中ほどで曲率がゼロになって向きを逆にしています。 それはよいのですが、上の方でも下の方でもゼロになります。 このサインカーブは滑らかで、見た目にもなだらかですが、曲率はこんなにも波打っています。
: とにかく、2つの曲線とを重ねてみました。 ぴったりとはいきませんが、2曲線は似ています。
似てはいるものの、の法線がすなおでないのが気になりますね。
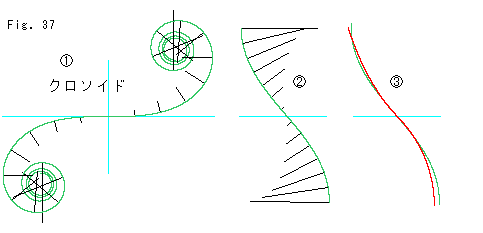
Fig.37をご覧ください。
上のFig.34のになじめそうな曲線をさがしていると、クロソイドというのがありました。
: これがクロソイドです。 その曲率は曲線の長さに正比例しています。 渦になって無限から無限へと延びている中間で曲率がなだらかにゼロになっています。
: その中ほどをとって、ちょっと拡大したものです。
: 向きを合わせて重ねたところです。 これも完全には重なりませんが、継ぎ目付近では十分足りています。
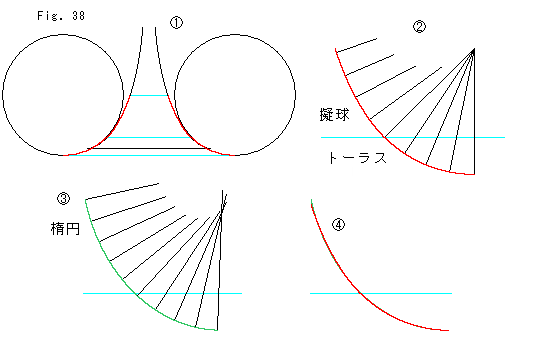
Fig.38をご覧ください。
こんどは擬球とトーラスです。
: 上側はこれまでと同じ範囲にして、下側はトーラスの天底までをとって、近似曲線を作ります。
: 擬球とトーラスを継ないで、法線を立てたところです。 曲率の変化はなだらかです。
: ふつうの楕円の部分です。 法線がのとよく似ています。
: 2つの曲線とを重ねたところです。 ぴったりですね。
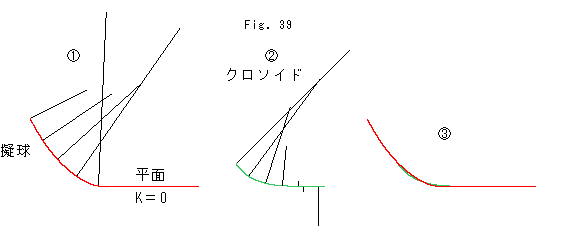
Fig.39をご覧ください。
: 擬球の底部にFig.33のように平面を継いだところです。 平面の曲率Kはゼロです。 ほぼ垂直に立っている法線の実際の長さ(=K)はものすごく大きいのです。
: 平面との境界の近似曲線としてクロソイドを利用します。 しかし、描いてある法線は1/1000に短縮したものです。 そして平面に似せようとするところでは、曲率がゼロになった後すぐに下側へ大きくのびていきます。 これは不自然ですね。
: ともかく、赤い曲線に重ねてみたところです。 おおむね好いところに見えます。 しかし、クロソイドに気がかりなところがありますね。
まてよ。 平面曲線である母線で見てきましたが、この場合は曲面のままで曲率を見たほうがよいかも知れません。 調べてみましよう。
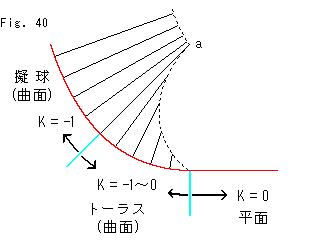
Fig.40をご覧ください。
曲率が -1 から 0 へとジャンプせずに移っています。 しかし、曲率を表している法線の先端を点線でなぞってみると、そのaのところが折れ線のようになっています。 どうやら、曲率の微分とか、曲率の曲率といったものを考える必要があるようですね。 また、トーラスのところでは曲率が一定ではないので、どんな幾何が利くのか私たちにはわかりません。
それに、擬球の方からトーラスを経て下ってくると曲がりがなくなって、先にもいったように何かしら馴染みにくい硬さを感じさせます。
さて、滑らかな曲線(母線)からなる回転曲面は、母線どうしが回転軸を切らないかぎり、滑らかです。 この考えで、「私たちの継ぎ目のある曲線は、滑らかな曲線と近似しているのだから、それでできた曲面は滑らかだといってもよい」としたいとすすめてきました。 しかし、どの程度の近似なら許すのかを考えておかねばなりません。 ともかく、数学的には滑らか（級）でないことは確かですが、それでいて滑らかに見えるわけがわかりました。
いい方をかえてみると、こうなります。 私たちの2つの母線は継ながれて連続しています。 その継ぎ目は
級の滑らかさがあるといえます。 そして、それで足ります。
双曲平面と楕円平面とユークリッド平面を自由に行き来できるオモチャを作ろうとしてきたわけですが、滑らかであろうとなかろうと、私たちの紙細工上では異なる世界を自由に行き来できます。 そして、境界線上で立ち止まってしまうことさえしなければ、三平面を遊戯的にも数学的にも十分楽しめます。
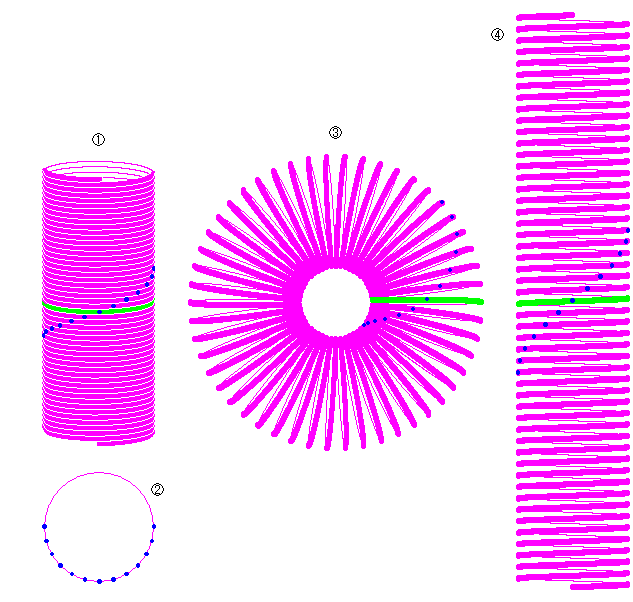
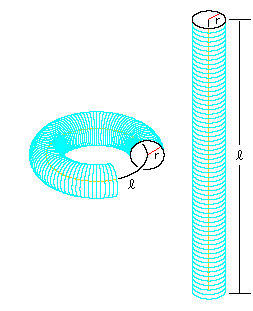
この章を閉じようとしたときに、100円ショップでスプリングコイルのおもちゃを見つけました。 右図をご覧ください。
がそれです。 青いスポットは、紙の上に引いた直線を移して描いたものです。
は、青いスポットを上から見たところです。
は、このコイルの両端を継ないだところで、トーラス状になります。 そこに並んでいる青いスポットは測地線上にあるといえないでしょうか。 そんな想いにかられたのは、Fig.31のように円筒を曲げてトーラスにしても、面積と中心線の長さは変わらないからです。
は、そのトーラスのチューブの中心線の長さに合わせてを上下に引っ張ったところです。 上の方のFig.31と見比べてください。（Fig.32とではありません。）
残念ながら、の青いスポット列は測地線上にはないと、九大の山田光太郎先生にいわれました。 そうすると、Fig.33の水色の領域内の直線も同心円も間違っていることになります。
いつか、きっとトーラス上のまともな測地線を描いて見せます。