双曲的非ユークリッドの世界(平面)のモデルの1つに上半平面というのがあります。 ポアンカレやクラインの円板のように双曲平面を一望に見せるものではありませんが、計算がしやすいとか、ホロサイクルや擬球との関係を見たり、とくに無限を考える上で有用です。 上半平面は記号で、よく
と表現されます。 ここでは、上半平面という平面が、どのように伸縮されたものであるのか、そこでは直線や距離がどうなっているのかを見ます。
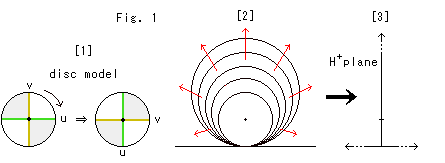
Fig.1をご覧ください。
ポアンカレの円板モデルには馴染みがあるので、まずは、その円板を変形して上半平面をつくってみます。
[1]: 円板モデルを右へ90
回転します。
[2]: そして、中心と下端を固定して、図のように無限に広げます。
[3]: すると、下側は水平な直線になり、そのほかは無限の彼方へ行ってしまいます。 こうして、上半平面ができ上がります。
(上半平面をポアンカレ円板から作る方法は他にもいくつかありますが、あとの方で見ます｡)
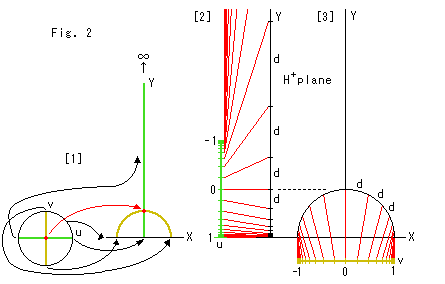
Fig.2をご覧ください。
ポアンカレの円板モデルと上半平面との対応関係です。 円板の縦横の軸をuv軸、上半平面の縦横の軸をXY軸と表わすことにします。
[1]: u軸は、正の側(右端, u = 1)をX軸上につけて、Y軸(y>0)に移ります。 u軸の負の側(左端, u = -1)は、上半平面の無限に上の方へ移ります。 v軸は、X軸にではなく、X軸上の半円になります。 上半平面では、すべての双曲的直線はX軸上の半円かX軸の上に立つ直線になります。 それにつれて、円板モデルの原点(中心)は、赤い矢印のようにうつります。 X軸になるのは、円板モデルの円周(無限遠直線)です。
[2]: u軸をわざと縦に描いて、双曲距離を0.5ずつに刻んでY軸との対応を赤い線でむすんでみたものです。 Y軸上のd(=双曲距離0.5)は対数目盛りになっています。 (対数目盛りにゼロはありません｡)
[3]: v軸をわざと横にねかせて、対応点をむすんでいます。 これも双曲距離0.5で刻んでいます。 双曲的直線である半円の左右の目盛りは、対数目盛りに似ていますが、そうではありません。
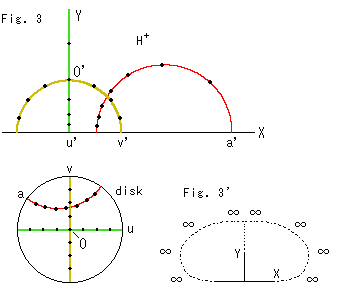
Fig.3をご覧ください。
同じ色の線が対応しています。 赤い曲線はどの軸に乗らない双曲的直線です。 黒いスポットは、ポアンカレ円板上でユークリッド的に等間隔にとった点の対応点です。 この対応点が半円上で左右対称になるのは、Y軸を対称軸とする半円になる場合かぎられます。 端点a,u,vは、それぞれ端点a',u',v'へ移っています。
Fig.3'をご覧ください。
ポアンカレ円板の左端(u = -1)は上半平面の上方へ行ってしまうといいましたが、かならずしもそうは断言できません。 円板の左端もその円周上にあるのですから、X軸へ移るはずです。 しかし、それでは辻つまが合いません。 実は、すでにこの問題は巧く回避されています。
上半平面は、円板モデルと同様に、すべての方向に開かれています。 X軸はふつうの双曲的直線ではありません。 全体の様子をこのFig.3'のように想像してもかまいませんが、次のようにくくった方がわかりやすいでしよう。
ポアンカレ円板は境界(円周)を完全に描くことができる開円板であって、それを別の格好の開平面にしたものが上半平面である。 上半平面の境界は、ほころびたものではなくて、その一部しか描かれていないだけであると。
そして、円板の内部から左端に辿りつくことは絶対にできないのですから、その左端の行き先を追うことは意味がないともいえます。 私たちの視界内では、X軸は半径無限大の円周の底部であり、Y軸はX軸上にある半径無限大の半円の裾です。
上半平面のX軸も無限遠直線ですから、それに沿った距離を定めることはできません。 ですから、X軸には目盛りはないのです。 軸に目盛りをほどこせるのはY軸だけです。 だからといって、上半平面上(y>0)でX軸方向の距離がいえないというのでは、もちろんありません。
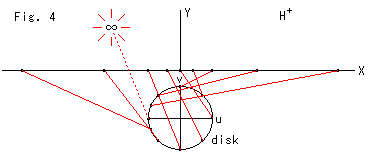
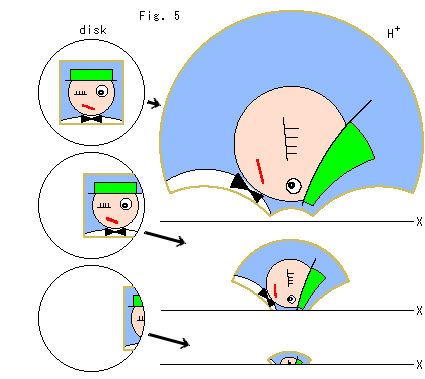
Fig.4をご覧ください。
ポアンカレ円板の円周上の点が上半平面のX軸上のどこへ移るのかを見てみたものです。 見やすくするために、円板を上半平面の真下へおきました。 赤い線が対応点をむすんでいます。 それが捩れているのは、円板を90回転させていないからです。 上半平面のX軸には目盛りをほどこすことはできませんが、同じ無限遠であるポアンカレ円板の円周との 1:1 の対応が定まっています。 ただし、円板の左端だけは例外です。 その例外的な対応(1:?)を花火のように描きました。
右のFig.5をご覧ください。
たわむれに描いたものですが、ポアンカレ円板と上半平面との関係がよく見て取れますね。 この絵とFig.1からの図を見比べてください。
上半平面そのものを見ていきましよう。
ポアンカレ円板と同様に、角についてはユークリッド角と同じですので、長さがについてです。 (計量のことは後でふれます｡)
上半平面上の双曲直線は、X軸に立つ垂線かX軸上の半円です。 なぜ、そのような形になるのということは、Fig.2などからいくぶん察しられますが、しかとはわかりません。 ポアンカレ円板モデルでは、なぜ直線が無限遠円周に直交する円弧かということにも、まだ答えを得ていません。 それらについては、おいおい当たっていくことにして、双曲距離がどのようになっているのかを見ていきましよう。
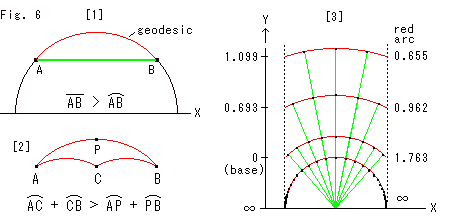
Fig.6をご覧ください。
赤い円弧に見えるのが双曲的直線す。 X軸に平行な双曲的直線はありません。
[1]: X軸に平行に見える緑色の線分は双曲的直線ではありません。 双曲的距離としては、赤い円弧ABの方が、緑色の線分ABよりも短い測地線(geodesic)です。 まさに「急がば回れ」です。
[2]: AからBまで行く場合、ルートA-C-BのほうがルートA-P-Bよりも長いのです。 双曲距離の足し算や引き算が成り立つのは、１本の双曲直線(垂線かX軸上の半円)上においてのことです。 Y軸がどこにあっても、これらのことは変わりありません。
[3]: 左側の目盛りは、X軸からユークリッド的等間隔にとった双曲距離です。 基準(base)点はX軸からユークリッド距離 y = 1 のところがです。 基準点から下の双曲距離を負にとってもかまいません。 右側の値は、赤い円弧(red arc)の双曲的長さです。 その長さ(距離)は、目にはあまり変わらなくても、X軸から離れるにしたがって小さくなっていきます。 黒いスポットは、円弧上で中点から左右に双曲的等間隔にとったところです。一番下の円弧は、X軸にのった半円で、その双曲的長さはむろん無限大です。 緑色の線は黒いスポットをむすんでみたものです。 それはX軸の1点に集中しています。 次に、これを見ます。
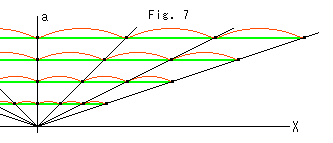
Fig.7をご覧ください。
直線aはX軸に垂直で、赤い"直線"はすべて同じ長さです。 緑色の"曲線"もすべて同じ長さです。 むろん、赤い線の方が緑色のより短いのです。 傾いた黒い直線はFig.6の[3]の緑色の線と同じものです。 それがX軸上の1点から放射状に出ていることは、X軸上では距離を定義できないということです。
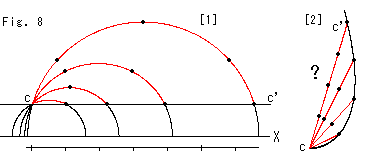
Fig.8をご覧ください。
[1]: 半円に見えるのは、共有点cを通る直線です。 その赤い部分の両端は、X軸にユークリッド的に平行な黒い線cc'上にあります。 赤い円弧上の黒いスポットは、一番小さい赤い円弧の双曲的長さを単位として円弧に沿った双曲的等間隔になっています。 つまり、点cから赤い双曲的直線に沿っていくと、視覚的直線cc'上の目的地へ早く到着します。 X軸の下に添えた目盛りと比べてください。 一番大きな赤い円弧で見ると、点cから円弧上を行けば黒いスポット4つをまたぐと直線cc'上の目的地に着きます。 同じ目的地へ行くのに、直線cc'上を辿っていくと、道程はおよそ1.7倍にもなります。
点cから同じ方向へ向かおうとするのに、出発する方向が距離によって異なっています。 黒い線cc'は、実際は直線ではなくて、曲がっているからです。
[2]: もしかしたら、双曲的非ユークリッドの世界の住人にはこのように見えているものかも知れません。
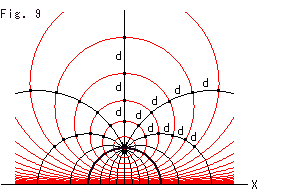
Fig.9をご覧ください。
双曲的同心円とその半径の直線です。 赤い同心円の双曲的間隔は一定のdに、黒い半径と半径の間の角は、
/8ずつにとってあります。 太い黒い半円は同心円の直径が連なったところです。
これから先、双曲空間におけるものとすぐにわかるときは、直線や距離の前にいちいち"双曲的"と書くのは、強調したい場合のほかは省きます。
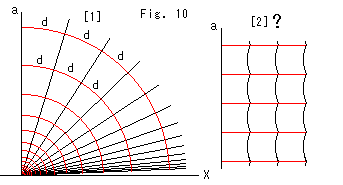
Fig.10をご覧ください。
[1]: 赤い線は直線です。 等間隔に描かれていますが同心円ではありません。 放射状にX軸に立っている黒い線は、垂線aに関しての等距離線です。 これらに挟まれている赤い直線は、すべて同じ長さdに切られています。 黒い等距離線は、垂線aだけが直線で、他は直線ではありません。 つまり、2本の赤い直線の間の傾いた黒い線に沿った距離は同じではありません。 ふつう、私たちが双曲幾何で距離というとき、それは双曲的直線(測地線)に沿って測ったものを意味します。 ユークリッド幾何と同じです。
[2]: 双曲的非ユークリッドの世界の住人には、[1]の様子はこう見えているのではないかと想像したものです。
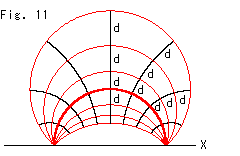
Fig.11をご覧ください。
欠けた円に見える赤い線は、赤い太い直線(半円)に関する等距離線です。 黒い線は赤い等距離線に直交した直線で、赤い太い半円上をユークリッド的等間隔にとっています。 等距離線の間隔は、すべて双曲距離dになっています。 赤の細い等距離線は、視覚的には円弧ですが、双曲的な円でも直線でもありません。
双曲的円は視覚的にも円として描かれますが、ポアンカレ円板と同様に、けっして境界(X軸)を切ることはありません。
下のFig.12をご覧ください。
4つの絵の下端はX軸です。 黒い曲線は赤い直線(半円)に関する等距離線で、両側をつねに同じ等距離dにとっています。 図を左から順に見ていってください。 赤い直線の右端aを固定して、左端を左の方へ動かしていったときの様子です。 一番左の図の左上の角
は、点aにおいて3つの曲線がなす角です。 この角は、赤い直線の左端がX軸上のどこにあっても変わりません。 図形はユークリッド的に相似拡大していくだけですから。 一番右の図は、赤い直線の左端が無限の彼方へ行ってしまった場合で、等距離線は円弧ではなく、見た目にも直線になっています。 等距離線と赤い直線は、無限遠で再会しているはずですが、定かではありません。
角を大きくしていき、90にしたときを想像してください。
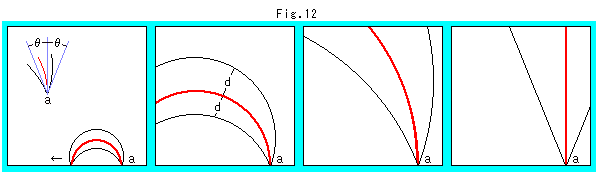
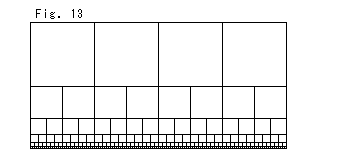
Fig.13をご覧ください。
上半平面をデジタル化したものです。 正方形のマス目の辺は、見た目に1つ上へ行くごとに2倍ずつ大きくなっていますが、双曲的には一定です。
Fig.14は、Fig.13のマス目を無理やりにそろえてみたものです。 モデルをこのように捉えたものが、実際の双曲平面に近いものです。
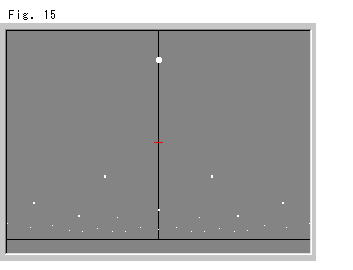
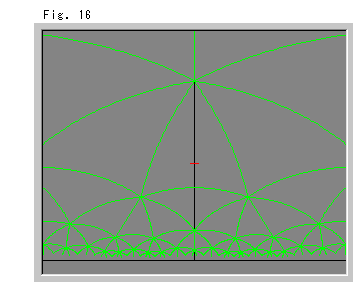
Fig.15をご覧ください。
等間隔スポット(隣り合うスポットの間隔が同じ)です。 スポットの大きさと間隔が、X軸から離れるほど大きく見えますが、X軸方向(Yは一定)では変わりありません。 Y軸上の赤い印-のところを基準点にとって描かれています。
右のFig.16をご覧ください。
Fig.15の隣り合うスポットを直線でむすんだものです。 どの三角形も内角2/7の合同な正三角形です。 つまり、タイル張りです。
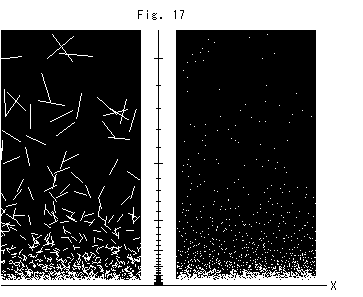
Fig.17をご覧ください。
上半平面に双曲線分とドットを散りばめたものです。 左側のは、どれも同じ長さの線分です。 真直ぐな線に見えますが、中心がX軸上にある円弧(半円の部分)です。 それらは上へいくほど、長くなり、まばらになって見えます。 右側のは、双曲スプレーです。 スプレーが上の方へいくほど薄くなっています。
線分もドットもX軸上では完全に稠密になっています。 疎密は、上下ではこのように変わりますが、左右(Yは一定)では変わりません。
さて、今後はときに応じて上半平面も使っていくことにします。