上半平面
とポアンカレ円板モデルの原点を通るホロサイクルとのかかわりから無限を考えてみましよう。
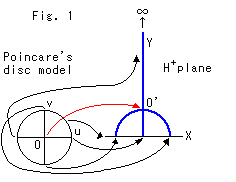
Fig.1は、前章からとったポアンカレの円板モデルと上半平面との対応関係です。
つぎのFig.2からFig.6までをシリーズに見てください。
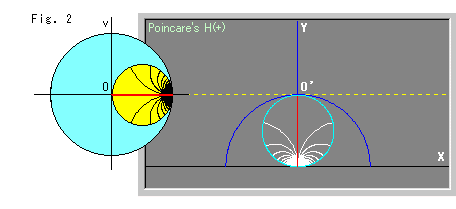
Fig.2をご覧ください。 左上の空色の円Oが、ポアンカレの円板モデルです。 その中の黄色の円が原点Oを通るホロサイクルです。 ホロサイクルの中の黒と赤の線は、円周上を円周に沿って等間隔にとった半径です。 このホロサイクルを右側の上半平面へ写していきます。 写されたホロサイクルの円周は空色で描かれており、その中の白と赤の線は半径で円板モデルのそれと対応しています。 上半平面上での半径は、すべてX軸上の半円の一部になっています。 黄色い点線は、点O'を通ってX軸にユークリッド的に平行に引いたもので、基準線です。
円板モデル上でホロサイクルを原点Oを中心にして左へ回していってみます。
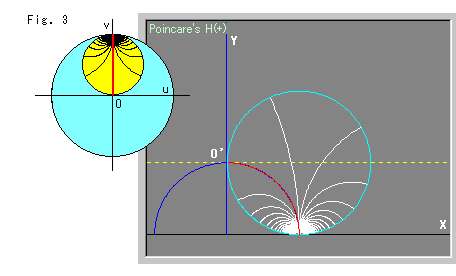
Fig.3は、ホロサイクルを90
回したところです。 上半平面上では、赤い半径がぴったりと青い半円の上に重なっています。 そして、ホロサイクルが見た目に少し大きくなっています。
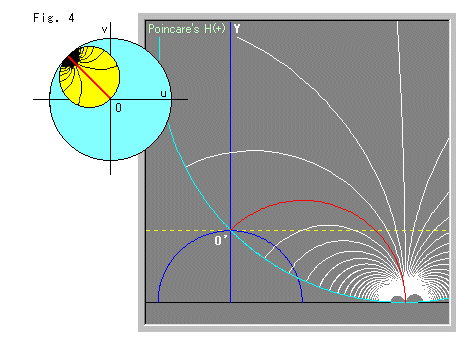
Fig.4では、ホロサイクルが 3/4 
回転していて、上半平面上では、だいぶん大きくなってきました。
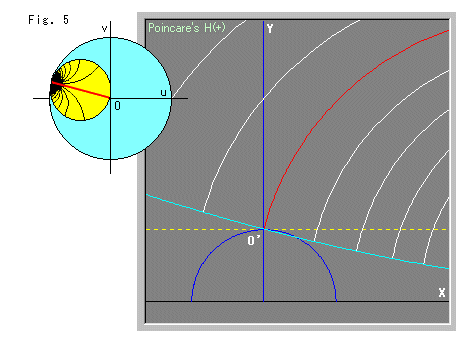
Fig.5では、ホロサイクルが 11/12 (165) の向きにあり、それは2に近い位置です。 そして、上半平面上では、とても大きくなっています。 大きくなったホロサイクルの円周の下端は見えませんけれども、X軸に接しているはずです。
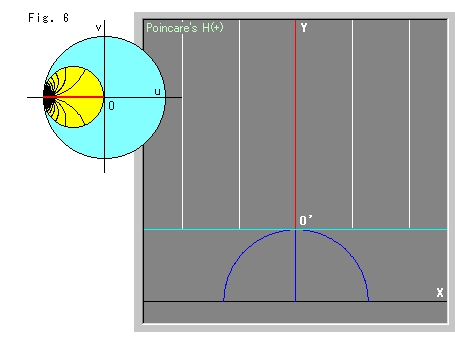
Fig.6をご覧ください。 円板モデル上のホロサイクルは、変わりなくおとなしくしていますが、上半平面上のホロサイクルは、破裂してしまいました！ その円周は直線に見え、半径は上の方の無限の彼方へと真っ直ぐに飛んで行ってしまっています。
いま、ホロサイクルは、Fig.1の反対側の位置にあります。 直立して並んでいる半径は、見た目にも等間隔です。
上半平面は、四方八方が開かれています。 下にあるX軸は無限の下方にあるものです。 上半平面モデルを長方形のようにイメージしてはなりません。
最初のFig.2のホロサイクルと、いま見ているFig.6のホロサイクルとを見比べます。 すると、円板モデル上では、v軸に関する鏡映になっていますが、上半平面上では、青い半円(v軸)を反転円とする反転という関係になっているのが分かります。 反転については、あとでふれます。
こんどは直接、X軸上で滑らせます。 滑らせるというのは、Fig.2〜Fig.6で見たようにホロサイクルの円周上の1点を点O'に固定し、円周の下端(ホロサイクルの双曲的中心)がX軸上こするようにして動かしてみることです。
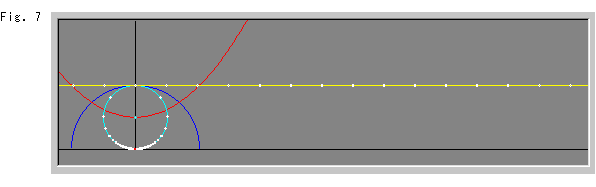
上のFig.7をご覧ください。 空色のホロサイクルの円周上に並んでいる白い点は、上端から円周に沿って双曲的等間隔にとったところです。 ホロサイクルの下端の赤いスポットは双曲的な中心で、つねにX軸上におかれます。 それぞれの白いスポットと赤いスポットの間の距離は、むろん無限大です。
黄色い直線は、空色のホロサイクルを反転させた方のホロサイクルの円周の下端付近です。 この直線状の円周の半径は、無限大になってしまっています。 その黄色い円周上に並んでいる白いスポットは、空色のホロサイクル上の白い点に対応しています。
赤い曲線は、空色のホロサイクルを滑らせたときの視覚的な中心の軌跡です。 黄色いホロサイクルのそれもこの軌跡の上を通ります。
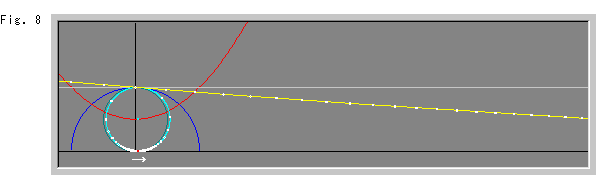
Fig.8は、空色のホロサイクルがほんの少し右へ動いたところです。 黄色い線をよく見てください。 もはや直線ではありません。 そして、その上の白いスポットが等間隔になっていません。 灰色の直線は、最初の黄色い線の跡です。 わずかに見える暗い緑の円は、最初の空色のホロサイクルの痕跡です。
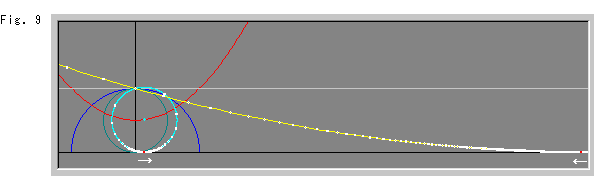
Fig.9では、黄色い線がX軸に接しているのが見えてきました。 その接点は空色のホロサイクルの赤いスポットに対応していて、黄色いホロサイクルの双曲的な中心ですので、同じ色の赤いスポットで印してあります。
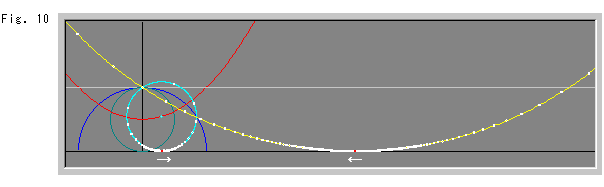
Fig.10を見ると、黄色い線が、明らかに円となってきました。
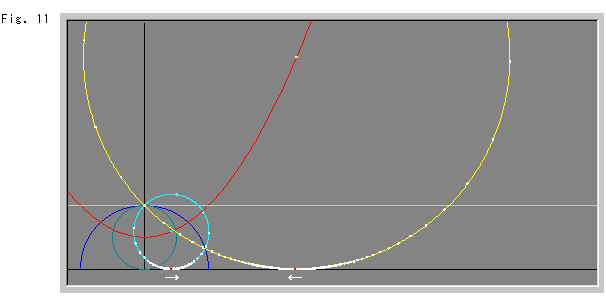
Fig.11は、黄色い円の視覚的な中心が、上半平面の開かれた上の方から降りてきたところです。
Fig.12になると、黄色い円の全体が姿を現しました。 まさしく円です。
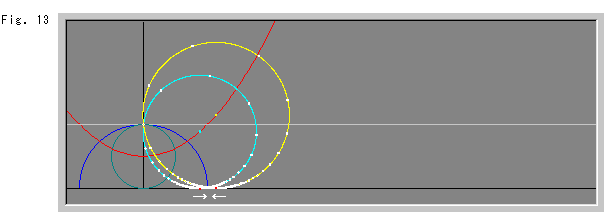
Fig.13では、空色のホロサイクルと黄色いホロサイクルの視覚的中心が接近してきました。 見てきたように、2つの円はつねに青い反転円上で交わっています。 それは、反転の性質から当然です。
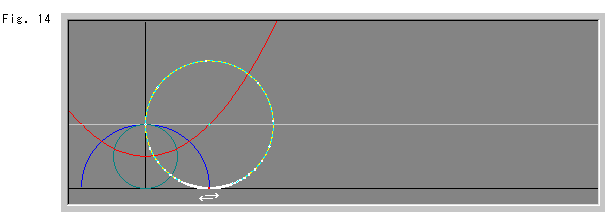
Fig.14では、2つのホロサイクルが重なっています。 これは反転がなされていないのと同じですが、反転円の内側と外側が交換されているのです。 そしていま、この二重のホロサイクルと反転円が同じ大きさになっています。
Fig.15になると、2つのホロサイクルは、赤いスポットをX軸上に引き摺りながら、たがいに通り過ぎていきます。 この後を見るには、ホロサイクルの色(空色と黄色)を交換し、矢印の向きを逆にして、Fig.15から逆にFig.7へとたどればよいわけです。
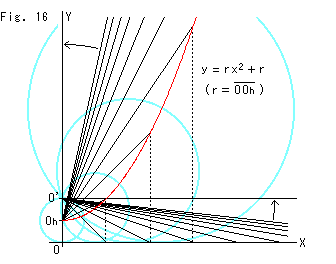
Fig.16は、Fig.15からFig.7へと逆にたどるときの、ホロサイクルの視覚的中心の軌跡を追尾したものです。 図中の式は、上半平面をふつうの平面だとして書いたものです。 つまり、双曲平面上の曲線としてでなく、ふつうのグラフだとすると、ホロサイクルの視覚的中心の軌跡は2次曲線だというわけです。
ホロサイクルの下端がX軸に接する点をふつうの等間隔に刻んだところと、ホロサイクルの最初の視覚的中心
を直線でむすびます。 また、X軸上の点に対応する赤い曲線上の点とホロサイクルの最初の上端O'を直線でむすびます。 ホロサイクルの下端がX軸上を右へ動いていくと、ホロサイクルの視覚的中心は、赤い曲線を登っていきます。 空色の円は、そのときのホロサイクルの様子です。
ホロサイクルの視覚的中心が赤い曲線上を限りなく登って行くと、どうなるでしようか？ 赤い曲線は、ふつうのスケールで2次曲線です。 2次曲線には漸近線はありませんが、その無限の先は点から見て真上になります。 ですから、ホロサイクルの視覚的中心も、真上の無限の彼方にあることになります。そのとき、ホロサイクルの視覚的半径は無限大になっているはずです。
一方、ホロサイクルの下端は、依然として右の彼方に行っているようですね。 しかし、実際は、どうなのでしようか？ Fig.1をもう一度見てください。 X軸は円板モデルの周に対応しています。 つまり、本当のX軸は、ふつうの直線ではなくて、無限の彼方の右にも左にも上にも通っているのです。
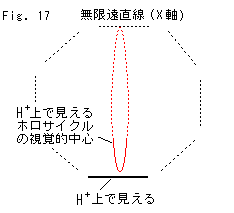
Fig.17は、その様子を想像したイラストです。 ホロサイクルの視覚的中心も下端(双曲的中心)も上方の無限遠になっています。 これがFig.7の状態です。
しかし、このイラストは勝手にイメージしたもので、裏付けは未だありません。
考えてきたことを復習してみましよう。
上半平面は、円板モデルと同様に、すべての方向に開かれていますから、ホロサイクルの視覚的中心も下端もけっして無限遠に達することはできません。 しかし、無限遠に達したと仮定すれば、Fig.7のようになると想像することは、不合理ではないと思われます。 「Fig.7はフィクションだ」というとき、それは、この考えに基づくものです。
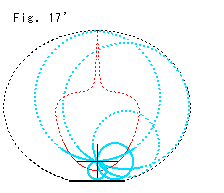
Fig.17'は、Fig.17にホロサイクルも含めて、こうかもしれない(It's might be.)と描いたものです。 ホロサイクルの視覚的中心の軌跡が妙な形になっていますが、あくまで放物線です。
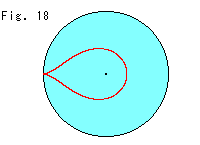
Fig.18は、Fig.16の赤い曲線を無限に伸ばして、ポアンカレの円板モデルに写してみたものです。 Fig.17'の想像画と似ていますね。 それは、上半平面も円板モデルも機能的に同じ双曲平面を表わしているのですから、当然です。 (上半平面上のホロサイクルの視覚的中心が、円板モデル上のホロサイクルの視覚的中心に対応しているのではありません｡） 円板の左端(無限遠)のところで本当にループになっているのかどうかは見て取れません。
Fig.7へ戻ってから先はどうなるのでしようか。 Fig.6の円板モデル上のホロサイクルを更に左へ回すと、上半平面では、対応するホロサイクルの全体が、左上の方から私たちの視界に入り降りてきます。
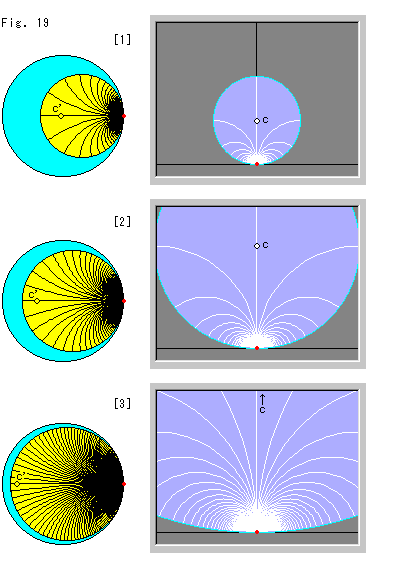
こんどは、上半平面上で、ホロサイクルの赤い下端(双曲的中心)を固定しておいて、視覚的中心を真上へ押し上げます。
Fig.19をご覧ください。 左側はポアンカレの円板モデルで、その中のホロサイクルが右側の上半平面の中のホロサイクルに対応しています。 円板モデル上のホロサイクルの中の小さなスポットc'は、上半平面上のホロサイクルの視覚的中心cに対応したところです。 半径は、ホロサイクルの円周に沿って、固定点と反対側の点を起点にした等間隔にとってあります。
ホロサイクルは、大きく描かれてあっても小さく描かれてあっても無限大です。 しかし、無限に大きなものの内部にある有限なものの大小をいうことはできます。
[1]は、ホロサイクルの視覚的中心cを上半平面上で上へ動かしたところです。 円板モデル上では、ホロサイクルが左へ膨らんで、大きくなって見えます。 その中で点c'が左へ動いています。
[2]は、さらに視覚的中心cを上へ動かしたところです。
[3]は、視覚的中心cをうんと押し上げたところです。 ただし、無限の果てまでではありません。 円板モデル上では、点c'が円板の縁の直ぐそばに見えます。
視覚的中心cが上方の無限遠へ行ってしまったら、どうなるでしようか。 X軸や円板モデルの円周に沿って距離を測ることはできません。 ホロサイクルは、上半平面の全体を占め、円板モデルと完全に重なってしまいます。 このとき、ホロサイクルの双曲的中心は定まりません。 それだけでなく、ホロサイクルとX軸との唯一の接点である赤いスポットの下端も、視覚的中心cとその対応点c'も意味を失います。 ホロサイクルは、赤いスポットの下端だけが開かれていたのが、いまは、ホロサイクルの円周全体が開かれているからです。 当然、等間隔の半径は描けません。
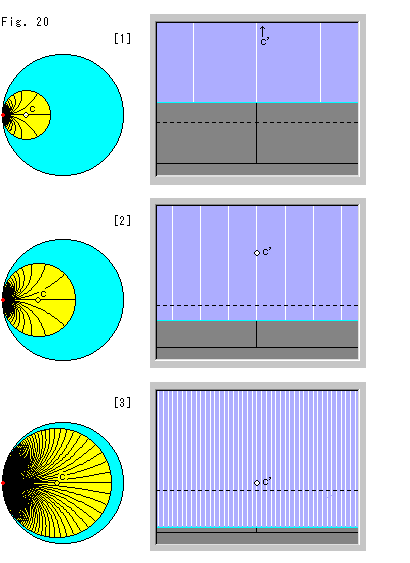
Fig.20をご覧ください。 Fig.19と同様にホロサイクルは、円板モデルと上半平面で、半径とともに対応しています。 円板モデルの左端は、上半平面の上方の無限遠に対応しています。 そこにホロサイクルの円周上の1点を固定します。 上半平面の図中に、この固定点は、私たちの描く上半平面に現れることはありません。 円板モデル上のホロサイクルの視覚的中心をc、それに対応する上半平面の点をc'と表わします(側にダッシュを付けています)。 円板モデル上のホロサイクルの視覚的中心cを右へ(上半平面では点c'を下へ)動かします。
上半平面上の黒い点線は、基準線(Y = 1)です。 半径の間隔は、Fig.19と同様に等距離にとってあります。
[1]は、円板モデル上のホロサイクルの視覚的中心cが右へ動き、上半平面の中で、対応するホロサイクルの下端が視界内に降りてきたところです。 上半平面では、視覚的中心cに対応する点c'は、まだ上の方にあります。 白い半径が等間隔に並んで真っ直ぐ上へ伸びているのが見られます。 その等間隔の巾は、上下で見た目に変わりありませんが、実際の双曲距離は上へ行くほど小さくなっています。 黄色いホロサイクルの黒い半径の実際の双曲的間隔も、円板モデルの縁にに近づくほど見た目よりも小さくなっています。 双曲物差しを思い出してください。
[2]は、円板モデル上のホロサイクルの視覚的中心cをさらに右へ動かしたところです。 半径の等間隔の巾が狭くなって見えますが、双曲的間隔としては、[1]と変わりません。
[3]は、円板モデル上のホロサイクルの視覚的中心cを円板モデルの中心に近づけたところです。 上半平面上では、点cの対応点c'が点線の基準線に接近しています。
円板モデル上のホロサイクルの視覚的中心cが円板モデルの中心に達したときは、Fig.19の[3]の後の状況と同じになり、ホロサイクルの双曲的中心は定まりません。
こう見てくると、円板モデルの円周は直線でもあり、上半平面のX軸は円でもあると、はっきりいえます。