空間の曲がり具合を表わすものに、計量と曲率があります。 ここでは、その計量を見ていきます。
ロバチェフスキーやボリヤイもすぐには世に受け入れられませんでした。 なぜでしようか？ 奇怪なことを言ったからでしようか？
彼らは、平行線公理の検討から入っていきました。 平行線は無限の彼方(私たちがけっして行けないところ)で交わるとか、角と距離とが依存しあうとか。 かなりの思考的妥協を強いられるものでした。 なによりも、彼らは、双曲幾何の三角法を証明しただけで、自分の創った(仮定した)幾何に矛盾がないことを証明したわけではありませんでした。
今日、数学者はモデルを使って研究しています。 対象は双曲幾何であっても、実際は、双曲三角法などを受け入れるほかは、ユークリッド幾何に拠っています。 そこで、よく「ユークリッド幾何に矛盾がなければ、双曲幾何にも矛盾はない」といわれます。 そして、「ユークリッド幾何の矛盾はいまだ見出されていないが、2000年の実績がある」とか、「ユークリッド幾何に矛盾がないことを証明することは不可能だ」ともいわれています。 それは、ゲーデルの不可能の証明というものに基づくそうですが、そんなものを私たちはまったく知りません。 いや、どうもスッキリしませんね。
私たちは、絶対的な真理とか完璧な論理を追究することには、興味もないし力もありません。 市民的な納得が得られればよいのです。 それにしても、あれこれと見てきましたが、なかなか明快とまではいきません。
リーマンの考えは、ロバチェフスキーらとはまったく違っていました。 双曲幾何に矛盾があるかないかは、検討の対象ではありませんでした。 彼は、空間を考察することから始めたのです。 地に足のついた考え方です。 あいまいな空想や仮定の上に展開したのではありませんでした。 リーマンは、平行線にかかわりなく、空間そのものとしてどんなものが考えられるかを探ったのです。 その空間の一つが双曲的非ユークリッドの世界だったというわけです。 リーマンによって、双曲的非ユークリッドの世界が怪物でもなく異端者でもなくなったといえます。
平面が曲がって曲面ができるように、曲がったとか歪んだといえる空間を考えることができます。 アインシュタインの相対性理論の話しにも出てきます。 私たちからすると、双曲的非ユークリッドの世界は、曲がった空間として捉えることができます。 それを示したのがリーマンです。
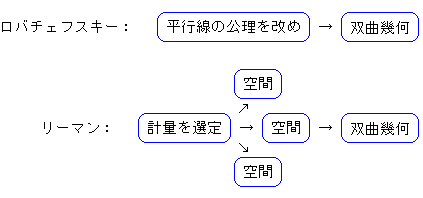
リーマンの考え方による解明の武器は、ガウスの微分幾何というものでした。 しかし私たちは、そんなものには踏み込まないで、例によって、果実だけを頂戴しましよう。
計量は顕微鏡的な物差しです。 日常生活でカップ一杯などいう計量とは、ちょっと違います。 ユークリッド平面(Euclidean plane)では、
と表わされます。 dsやdx,dyは、無限に小さい量で、dsは線素とよばれています。 
は、
ではなく、
のことです。 x,yについても同様です。 を面素ともよびます。 また、を表わす式は、微分幾何では第一基本形式とよんでいます。
この計量(1)は、ピタゴラスの定理を無限に小さなところに適用するものですね。 線素dsはミクロの世界のものですが、それが大きな空間の性質を表現しているのです。 微視的なものから全体の様子がつかめるとは妙な感じがしますけれども、そうなんです。 これは、積分することによって、はじめて具体的な長さになります。
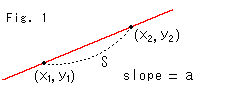
たとえば、こうです。 Fig.1の赤い直線はユークリッド空間の中にあります。 その直線上の点
から点
までのふつうの長さSを求めてみます。 直線の式は
です。 このままでピタゴラスの定理をつかえば、長さSはすぐに出せます。 しかし、式(1)によることにします。 式(2)の両辺を微分して得られる
を式(1)に代入します。 そして、整理すると
となります。 これを積分して、
とユークリッド平面での長さSが得られます。
ユークリッド平面でないときの計量(物差し)は、式(1)とは違ったものになります。 上半平面
での計量は
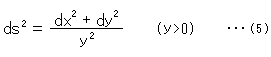
です。 こんどは分母にyがあるので、ちょっとややこしい。 この 1/y はユークリッド計量(1)につけられた重みといえるものです。 それは、ピタゴラスの定理からのづれの度合いです。 重みは、また、長さの密度とみることもできます。 この場合、重みづけはユークリッドの平行線公理の否定になっています。 曲がった空間は、重みが1でない空間です。
重みのはたらきを見ていきましよう。 y = ax + b とすると、式(5)は簡単に積分できて、2点(
,
),(
,
)間の双曲的距離Sは
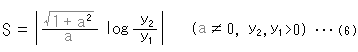
です。 xかyが一定なら、
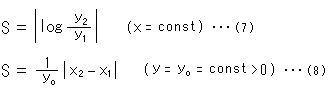
といったぐあいです。
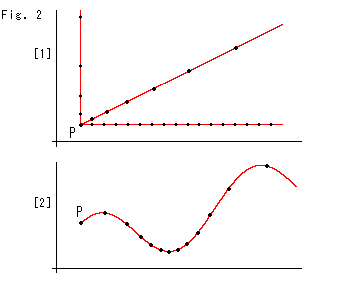
Fig.2をご覧ください。
上半平面上に描いてみます。
[1]: 赤い視覚的直線を点Pから3本引いて、点Pから双曲的等間隔のところに黒いスポットを印したものです。 式(6),(7),(8)をつかっています。 すべての黒いスポットの双曲的間隔は同じですが、X軸からの隔たりによって違って見えます。 視覚的に水平な直線上では等間隔の巾はどこでも同じです。 いうまでもなく、垂直な線だけが双曲的にも直線です。
[2]: 曲線に沿った双曲的等間隔の様子です。 X軸に近いほど間隔が縮んで見えています。
曲線の長さを精確に測るには、その曲線に沿う曲がった物差しが便利です。 式(5)は、いわば、曲がった空間に合う物差しを作るルールです。 そして式(6)などは、具体的に曲がったものを測る物差しです。“曲がった”というのは、見た目に真っ直ぐであっても、長さが均等に目盛られたふつうの物差しが使えないことも指します。
計量というものを知るために、それが具体的にどう効くのかを、いくつかのことで見ておきます。
上のFig.3をご覧ください。
上半平面を切り抜いて擬球をつくり、重みのはたらきを見てみます。
[1]: 上半平面から黄い範囲abcdを切り取りますす。 巾をX軸のところで2
にとって、垂直に切ります。 上端abでの双曲的な巾は2ではなく、その0.8157倍くらいになっています。 縦方向の長さは、ユークリッド距離で1のところを基準線Sにとって、上端で2になっています。 双曲的直線の例として3つの半円を描いておきます。
[2]: 黄色い四辺形abcdをX軸方向とY軸方向から絞って、実際の双曲的長さになるように変形すると富士山形のabcdになります。 それにつれて、3つの円弧が黒い曲線のようになります。 X軸方向とY軸方向だけに関しては、これで双曲的距離をユークリッド平面に移したことになるのですが、他の方向については不完全です。
ところで、円板モデルでは実際の双曲的な姿に近づけるために引き伸ばしました(Ch.16)。 ここでは、それと逆のことをしているように見えますね。 たしかに作業としては逆ですね。 しかし、X軸は基準線Sから無限遠のところにあるので、[1]と同様な長方形を基準線Sの下側につくるなら、引き伸ばしをすることになります。
[3]: この富士山の左右のadとbcをつないで擬球をつくります。 胴回りの長さはそのままでよいのですが、擬球の母線の長さが[2]の高さとちょうど一致するようにY軸方向にさらに圧縮します。
[4]: そうしてできた擬球です。
: 富士山[2]からつくったので、尻尾のほうがちぎれています。
: の側面です。
,
: こちら側へ,をすこし傾けたものです。
: 真上からを見たものです。 黒い曲線は[1]の円弧に対応するものですが、[1]の最大の円弧だけが閉じたループになっています。
このようにして私たちは、上半平面から擬球を手に入れることができました。 どちらもモデルですが、後者では曲面上の測地線を直線とみなすということだけが条件です。 擬球上での長さは、面に沿っていけば、ふつうの物差しで測ることができます。 それでは、重みはどうなっているのでしようか。
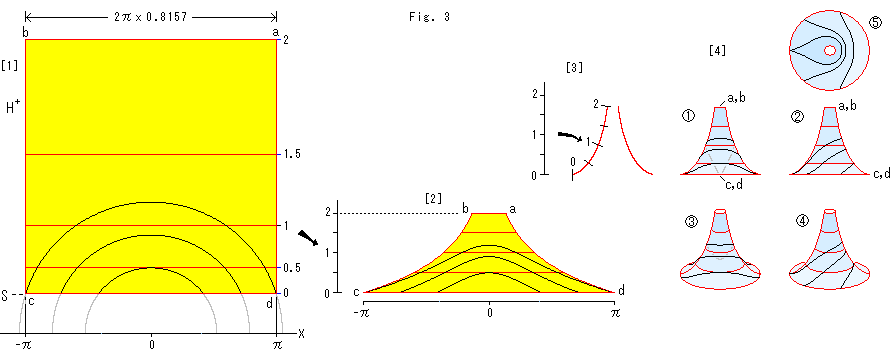
Fig.4をご覧ください。
擬球上の点(x,y,z)とr,
の関係です。 は擬球の開口部を斜めから覗いたものです。 はZ軸を、はX軸を画面に垂直にしたところです。
さて、擬球の式は
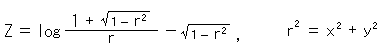
です。 その計量は、ユークリッド空間におけるものですから、式(1)にならって
と書けますが、このままでは重みの姿は見えません。 これに擬球であるx,y,zの関係を入れて、極座標(r,)になおすと
となります。 は2文字で表わされています。 このrを
と変数変換すると、
です。 あわせて、もuと書替えると、式(10)は
となります。 これは、上半平面の計量の式(5)とまったく同じ形ではありませんか！
そうです。 uv平面は、ほかならぬ上半平面です。 もっとも、上半平面の全体をカバーするには、uの 
といった制限をはずしておかねばなりません。 ただし擬球にもどすと、Ch.18で見たように、多層擬球になります。 ですから、上半平面と擬球面がきっちり対応するのは、やはり に限られます。
右図のは半径としてのvとrの関係で、はuv-平面としてのv軸を見たものです。
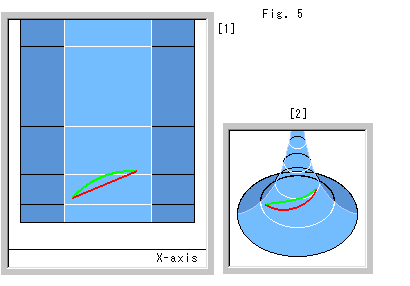
Fig.5をご覧ください。
擬球上の直線の様子はCh.18で見ましたが、それを上半平面との関係で見てみます。 擬球は、その曲面を面とみなし測地線を直線だとするのですから、擬球上では真直ぐなふつうの直線は1本もありません。
[1]: 上半平面上に見た目に真っ直ぐな赤い線分があります。 その両端を緑色の双曲的線分(円弧)がむすんでいます。
[2]: 対応する赤と緑の線分の擬球面上での様子です。 こんなふうに赤い線分は実際は曲がって凹んでいるわけです。 緑色の線分は、すこし曲がって見えますが、測地線です。 ([2]は、[1]に比べ約2倍の大きさに描いています｡)
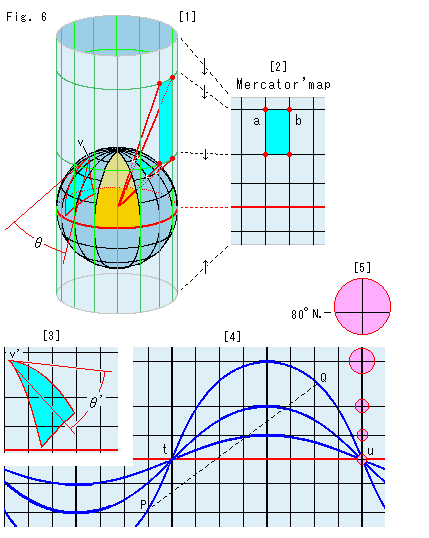
Fig.6をご覧ください。
世界地図でちょっと考えてみます。 メルカトールの世界地図が有名ですが、他にも沢山の種類があります。 同じ地球でも、地図ごとに図上での距離の測り方(計量)が違います。 これが、実体に変わりがなくても、モデルごとに計量が異なることに相当します。 (いろいろな世界地図が、Cartographical Map Projections などに公開されています｡）
[1]: Ch.4でもとりあげた円筒投影法です。 このままでは精確なメルカトール図にならないので、矢印のように上下から少し圧縮します。
[2]: メルカトールの地図(Mercater's map)です。 広げて見るのは[1]の円筒の外側です。 内側を見たのでは、地球の中に入って地表を見ていることになります。
経線(縦線, 子午線)と緯線(横線, 卯酉線(ぼうゆうせん))は、ともに/8 の間隔にとってあります。 それは、計量をデジタル化して目に見えるようにしたものですね。 上半平面では、Fig.3の青い線がこれに相応します。
この地図上の見た目の距離が実際の距離でないことは、だれでも知っています。 子午線間の距離は、赤道上で約2500Kmですが、上へ行くほど狭くなっていて、北緯67.5
)の点a,bでは、950Kmくらいしかありません。 緯線間の距離は、見た目には上へ行くほど大きくなっていきますが、緯度としては等間隔です。
角については、いわゆる等角写像になっています。 擬球上と上半平面との関係も等角写像になっています。 球面(地球)上の2曲線の交角が、地図上の対応する2曲線の交角と一致します。 角が一致するというのは、地図上で真っ直ぐな定規で測った方位角ではありません。
[3]: 水色の三角形は、球面上に直線(大円)で描かれた三角形(球面三角形)を地図上に写したものです。 頂点vが頂点v'に移っています。 頂点vの角と頂点v'の角'は一致しています。 他の頂点についても同様です。 球面三角形の内角の和は、より大ですから、この地図上の三角形の内角の和もより大です。 見た目に大きくなって歪んでいても、等角写像だからです。 メルカトール地図が重宝される最大の理由です。
[4]: 青い曲線は、よく見慣れた赤道上の2地点をむすぶ大圏コースです。 点tと点uは対心点(球の直径の両端)です。 サインカーブに似ていますが、そうではありません。 赤道のところで/8ずつ傾けています。 赤道も子午線も大圏コースです。 点tから点uまでの大圏コースに沿った距離は、コースによって見た目には大きく違いますが、実際は同じです。 点線PQのように(地図上で)真っ直ぐな線を航程線といいます。 これに沿って進めば、確実に目的地に到着できます。 大圏コースから外れているので時間のロスですが、これもメルカトール地図の大きな利点です。
[5]: 同じ面積が高緯度になるほど大きく見える様子です。 北緯80では、赤道のところのおよそ35倍にもなっています。 その大きなピンクの円では、中心が下にずれているのがはっきり見られます。
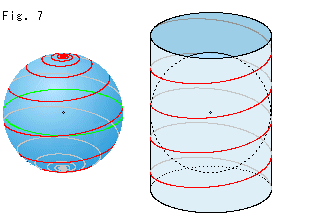
Fig.7をご覧ください。
メルカトール地図の上を斜めに真っ直ぐにどんどん進んで(航程線上を)行くと、地球をぐるぐる回って、北極か南極へと向かいます。 しかし、けっして極点にたどり着くことは、できません。 無限回らなければならないからです。 地図を円筒にしてコースを見ると、その様子がよくわかります。 メルカトール地図は、有限であった地球の表面を上下に無限の広がりをもったものにしているわけです。
赤道から上だけを見ていると、上半平面によく似ていますね。 世界地図の実体はまるい地球です。 いま仮に、それが目に見えないものであったとしても、地図さえあれば、実体を把握できます。 たしかに、そうです。 しかし、そうと知っていても、頭に電圧をかけないと見て取れません。 双曲平面の実体とモデルとの関係もこれと似ています。
計量の話しにもどします。
立体は、ふつう3つの文字x,y,zなどをつかって表わします。 半径1の球面(sphere)なら、
と書きます。 しかし表面だけを考えるなら、2つの文字でたります。 現に地球の面も世界地図も経度と緯度の2つだけで表わされています。 でも、世界地図にはいろいろな種類があるように、同じ立体でも、2つの文字で表わす方法は一定ではありません。 2つの文字で表わすということは、立体の面を平面にしてしまうことと考えてよいのです。 曲面の計量も2つの文字で表わされます。
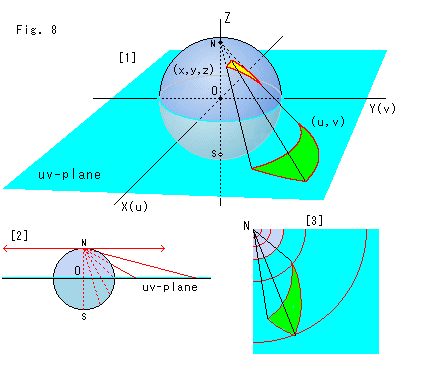
Fig.8をご覧ください。
これは立体射影とよばれているもので、球面(sphere)上の点(x,y,z)をuv平面に写す一つの方法です。 立体射影には、uv平面を球の下に敷いたものもありますが、ここでは球の赤道面におきます。 uv平面は天の赤道面に相当します。
球面上の点が、北極Nから出た射影線によってuv平面上に写されています。
[1]を見ると、球面三角形がuv平面上に射影されて大きくなり歪んでいます。 しかし、これも等角射像で、三角形の頂点の角は球面上のそれと一致しています。 球面上の三角形とuv平面上の三角形の色が違うのは、たがいに裏返しになっているからです。
[2]は、uv平面を水平にしてX(u)軸方向から見たものです。 赤い射影線を水平から30ずつ下へ傾けています。 (左側は省いています｡) 球の赤道を境にして、北半球上の点は外側のuv平面へ、南半球上の点は内側のuv-平面へ写ります。 射影線を下から上げていって水平(z = 1)になったときは、対応する点が右の方の無限遠にあるようですが、無限遠点には定まった場所はなかったのを思い出してください。 赤い矢印は、それを強いて描いたものです。 x,y,zの値にはプラスマイナス1以内という制限がありますが、u,vにはそんな制限はありません。
[3]は[2]の部分を上から見下ろしたものです。（[2],[3]は、[1]の1/2尺です｡）
簡便のために、球面の半径を1とします。 すると、このuv平面上の計量(線素ds)は、微分幾何の第一基本形式というものを使うと、
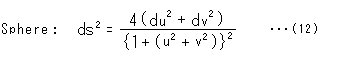
と表現されます。
このuv平面は球の性質をもった平面(plane with spherical character)です。 uv平面上での長さをこの計量で測れば、球面上での長さが得られるわけです。
式(12)をユークリッド平面の計量の式(1)と見比べて、
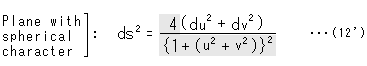
のように、変わっているところに影をつけてみました。 これを開平した
が重みです。
それでは曲がり具合を効かす重みを反対にして
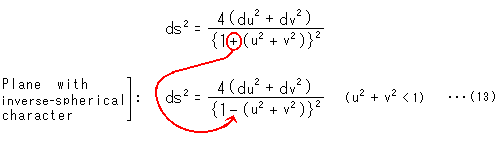
のようにプラスをマイナスにすればどうなるでしようか？ それは、反球面の性質をもった平面(plane with inverse-spherical character, antisphere)とでも呼べるものになります。 この計量をもったuv平面は、Fig.8の[1]のように無限に広がったものではなく、半径1の円の内部になります。（上の式で
になると、線素dsが負になってしまいます｡）
これは、まさにポアンカレ円板の計量です。 反球面の性質をもった平面に、この計量で測った最短コース(測地線)を直線とみなすという約束をつけておきます。 すると、反球面の性質をもった平面は、実際の双曲平面と同じもの、つまりモデルになるわけです。 そのモデルが、この場合はポアンカレ円板です。
上半平面の計量の式(5)での重み 1/y とポアンカレ円板の式(13)での重みは異なっています。 重みは、モデルであるところのuv平面（式(5)ではxy平面）につけられたもので、双曲的平面それ自体の曲がり具合を表わすものではないからです。
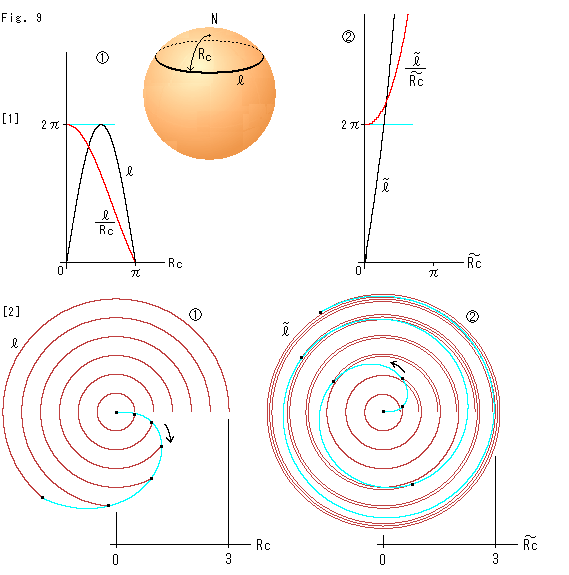
Fig.9をご覧ください。
上の式(13)を見ただけでは、いま一つピンときませんね。 反球面と名づけたモノを目で捉えましよう。
[1]: グラフで見てみます。
: グラフの黒い曲線は、球面上の円の周(緯線の長さ)
が球面半径(北極Nから緯線までの距離)Rcとともに変わっていく様子です。 円の周はいちど大きくなったあと、小さくなり最後にゼロになります。 赤い曲線は、刻々の円周をそのときの球面半径Rcで割ったものです。 ふつうの平面上では半径が変わっても、円周と半径との比は一定の2ですが、球面上ではこうなります。
そして注目すべきは、この性質は球面上のどこを起点にとっても変わらないということです。
それでは曲面上のあらゆる点で、面に沿った半径がどこまでも大きくなることができ、それとともに円周が際限なく大きくなるという、球とは逆の性質をもったモノはどうでしようか。 それはいうまでもなく、双曲的な平面です。 そんなモノをふつうに描くことはできませんね。
: でも、グラフでなら簡単です。 
と
は、ともに双曲的長さです。 このグラフは双曲モデルからと同じ考えでつくったものです。 双曲モデルとしてはどんなモデルでも、当然ですが、同じグラフになります。 そして球面と同様に、双曲平面としての原点Oもどこでもよいのです。
右図の<1>はポアンカレ円板で、<2>は上半平面です。 いずれもこれまでにも見たものですが、かってな点を双曲的作図の原点Oにとっていることに注目してください。 上半平面の緑色の垂線上の黒いスポットは、ポアンカレ円板の中心に対応する点です。 曲線は、双曲的等間隔の同心円と30間隔の放射線(双曲直線)です。
[2]: 半径に応じた円周のあるがままの長さを弧や渦に描きます。
: 球面半径Rcを等間隔に赤道までとって、ふつうの平面に描いたものです。 北極Nから赤道までまでの距離Rcを3としています。 円弧の長さは、半径Rcに応じたもとの円周の長さです。 水色の曲線は、Rcを連続的に変化させたときの円弧の先端の軌跡で、矢印はその伸びて行く方向です。
: 同じ要領で双曲円弧を描いたものです。 こんどは渦になっています。 双曲的長さそのままで作図しています。 水色の曲線が、とは逆に左回りに伸びていっています。
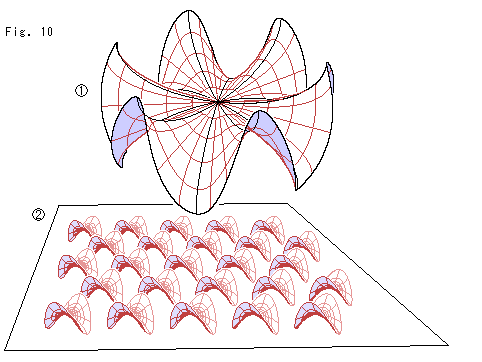
Fig.10をご覧ください。
上のFig.9の最後にある渦のが一重になるように円周方向に引き伸ばします。
: すると、前にも見たあの波打った曲面になります。 しかし、このような曲面は正しい双曲平面ではありません。 双曲幾何の本当の平面は、その上のすべての点の近傍がこのようになっているとうものです。 正確なのは、あのベルトラミーの擬球です。 けれども、この波状曲面は正確なものではありませんけれども、私たちのいう反球面の姿態をよく表しています。 ピタゴラスの定理が成り立たなくなる式(13)の重みをつけたから、こんなものが現れたのです。
: 双曲平面上のいたるところが鞍形状になっている様子をマンガ風にイラストしたものです。 ここでモデルというものが、どんなに素晴らしいものかということに、あらためて気づきます。 それは、こんなマンガの状況がふつうの平面上に正確に表されているものです。
これで2つの式(12)と(13)の違いが、かなり掴めました。 しかし、それは後者が双曲平面であることを知っていてのことでした。 式そのもの差異を見てみましょう。
式(12)は極座標で
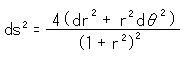
と書けます。 式(13)も同様にします。 そして、を一定（d = 0）にして、直線上だけで動かします。 すると、球(sphere)の式(12)と反球面(antisphere)の(13)は、それぞれ
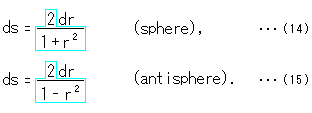
となります。 こうすると簡単に積分できます。 水色で囲んだところが重みWです。
原点Oからの長さSは
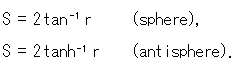
と得られます。 この2式は、ふつうのtanと双曲線関数のtanhで、hが付くかつかないかの違いだけです。
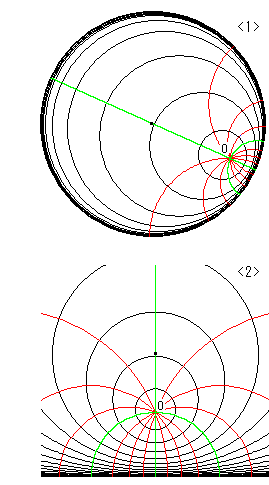
それでは、ポアンカレ円板(反球面の性質をもった平面)とふつうの球面とのちがいを見てみます。
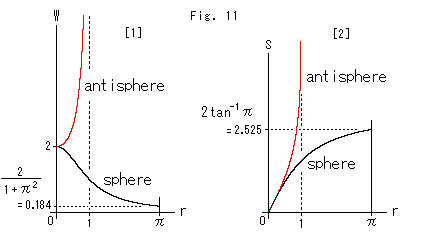
Fig.11をご覧ください。
黒い曲線が球(sphere)のもので、赤い曲線はポアンカレ円板(antisphere)の場合です。
[1]: 重みWの変化を見たものです。 球では、黒い曲線のようにrが大きくなるにつれて重みWが軽くなっていき、一定のところで止まります。 ポアンカレ円板では赤い曲線のように、逆に重みWが急激にきつくなって、際限なく大きくなっていきます。
[2]: 原点Oからの長さSについて見たものです。 黒い曲線も赤い曲線も上へと延びていて、対称的によく似ていますね。 しかし、球の黒い曲線は一定のところで止まっています。
これらのグラフも原点Oがどこにあっても変わらないことを忘れないでください。
ところで式(14),(15)を見ると、式(14)の分母のrを虚数
rに置き換えたものが式(15)の分母になっていることに気付きます。 しかし、これは双曲幾何は虚球面の幾何だといわれるところのものではありません。 なぜなら、分母だけをいらったからです。 これについては後でまた見てみます。
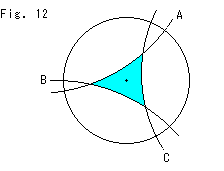
Fig.12をご覧ください。
よく双曲構造を与えるといわれているのは、どのようなことを指すのでしようか。 ふつうの紙の上に円とそれに直交する3つの円弧A,B,Cを描いて、水色のくぼんだ三角形をつくります。 円の内部には、計量(13)を使うという条件(環境)を与えられているとします。 すると、3つの円弧は直線とみなされます。 そして、水色の三角形は、もはや歪んでいなくて、計量(13)で“ふつうに”測られます。 その結果、三角形は、3辺が直線であるのに、その内角の和が2直角より小さくなります。 これは、いままでの話から当然ですが、ロバチェフスキーの平行線の公理から出発したのではありません。 勝手に計量を選んだのです。
結果が双曲幾何をもったものになることが分かっているので、このようにすることを双曲構造を与えるなどというのです。
ここで注目すべきは、実体がどうのということとは無関係に、どんなものにでも双曲構造を与えることができることです。(どんなものにでもといっても、ふつうは、なめらかな曲面を指しています｡)
実体は問題ではないというのも理解できなくはありません。 しかし、上の方で実体を指して反球面という言葉をつかいました。 それは、つぎのように考えてのことです。
たとえば、世界地図を眺めるとき、私たちは、上下の方は縮んでいて左右はつながっているんだというイメージ変換を頭の中で実行します。 ところが、そうして地図を見ても、地球儀を見るような感触を得ることはできません。 地球儀を手にしていれば、ことは簡単です。 実体である地球を把握することも困難ではありません。
双曲的非ユークリッドの世界のモデルは地図ですから、双曲的地球儀のようなモノがあれば、大いに役立ちます。 欲しいですね。 そんなモノをとことん追ってみましよう。 なにか出てくるかも知れません。
そんな思いですので、双曲平面を双曲平面とよんでおくだけでもよいのですが、具体的な実体を指した名前があれば、思考のたすけになります。 反球面は、そういった意味での私たち独自の造語です。
ロバチェフスキーらは、奇怪なものを発見したのです。 そのために、見出されたものが真なりや否やということになったのです。 リーマンの考え方にならって、私たちの方から奇怪なものを能動的に創ったときは、それが奇怪なのは当然です。 どこにも、不合理はありません。 その一つが、双曲幾何と一致するだけのことです。
ともかく、計量といったものに支えられたモデルの出現によって、双曲幾何が世人に受け入れられるようになりました。 そして、双曲的非ユークリッドの世界の神秘性を完全にではないにしても、実際的に拭い去られました。