あれこれと違ったモデルに出会いますね。 ひとつづきの相互関係を見ておくことにします。 しかし、上半平面から擬球を得たときのように、双曲空間の正体を覗くことは期待できません。 モデル間の移りあいを見るだけですから。 見てやろうの一環です。
射線を利用すると、双曲面モデル、ポアンカレ円板、クライン円板、上半平面、半球モデルの5つのつながりを一度に見ることができます。 ここでは、まず双曲面モデルとポアンカレ円板の関係を見て、それから他のモデルに触れていきます。
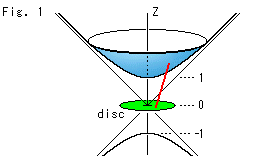
Fig.1をご覧ください。
ポアンカレ円板をuv座標で表わすと、その計量dsは先に見たように
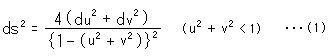
です。 これに対応するもととなる曲面は、回転面である直角二葉双曲面の片方
です。 これはCh.5でとりあげた双曲面モデルです。 球としての性質(計量)をもったuv平面の実体は球でが、双曲面はポアンカレ円板の実体ではありません。 対応がつくだけです。
双曲面の漸近面(円錐)の z = 0 のところにポアンカレ円板が水平にセットされます。 双曲面は無限に上へ伸びているのですが、見やすくするために図では途中で切っています。
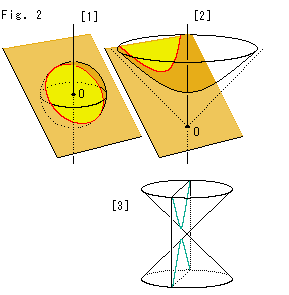
Fig.2をご覧ください。
[1]: 球をその原点O(中心)を通る平面で切ると、球面上の赤い直線(測地線)が得られます。
[2]: 双曲面も原点O(円錐の頂点)を通る平面で切ると、双曲面上の直線(測地線)が得られます。
球面と双曲面には、このような共通したところが沢山あります。 おいおいそれらを見ていくことになります。
[3]: 円錐をこのように平面で切っても双曲線はできますが、これと双曲面上の赤い双曲線とはまったく別物ですので、勘違いしないでください。
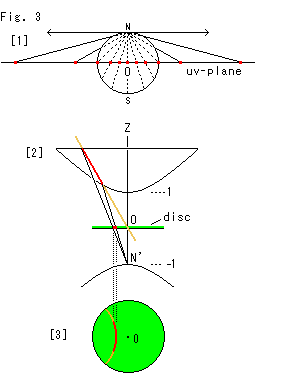
Fig.3をご覧ください。
[1]: 球面上の点をその北極Nから原点(中心)Oを通るuv平面(uv-plane)に射影している様子です。
[2]: 双曲面には球面のような北極がありません。 かわりに下側(z < 0)にあるもう一つの双曲面の頂点N'(z = -1)から射影線を引いています。 Fig.2の[2]を茶色の平面に平行な方向から見ています。 双曲面上の赤い線をポアンカレ円板に射影しているところです。
[3]: ポアンカレ円板を上から見たところで、双曲面上の双曲線が円弧になっています。 つまり、双曲面上では双曲線が双曲的直線です。
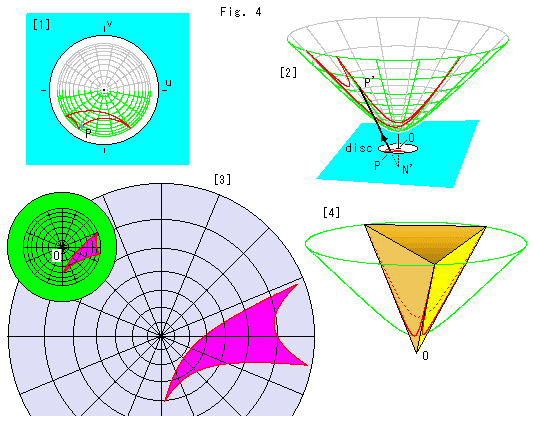
上のFig.4をご覧ください。
[1]: ポアンカレ円板に描いた双曲三角形です。
[2]: [1]の三角形を双曲面へ点N'からの射影で移したものです。 点Pが点P'になります。
[3]: 緑色の小さい円板はポアンカレ円板で、大きい紫色の円板は双曲面を真上から見下ろしたものです。 対応する矢車模様の格子をよく見ると、同心円の間隔が、ポアンカレ円板では外へ向かうほど小さくなっているのに対して、双曲面では逆に大きくなっているのが分かります。 これは、真上から見上から見てのことですから、実際にはもっと大きく、図の
倍近くなっています。
[4]: 双曲面上の双曲三角形は、原点Oを頂点とする三角錐に丁度はまりす。
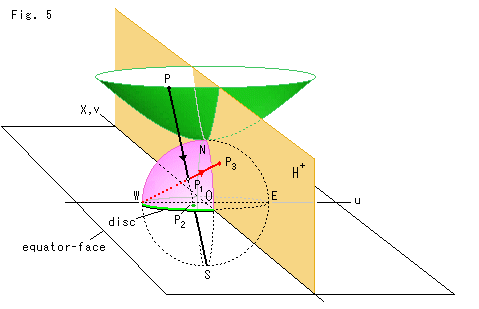
Fig.5をご覧ください。
4つのモデル（双曲面、半球面、ポアンカレ円板、上半平面）を一連につないでいます。
原点Oにポアンカレ円板を置いて、それに半球面をかぶせると、半球面モデルになります。 半球面モデルの天頂Nが双曲面の底になり、赤道がポアンカレ円板の円周になっています。
つぎに、双曲面と半球面を切る半平面を赤道面(equator-face)に図のように立てます。 その平面が上半平面
なります。 上半平面のX軸がポアンカレ円板のv軸に重なっています。
黒い矢線のように、双曲面上の点Pからから射影線を発射させるとします。 射影線は、(北)半球面とポアンカレ円板を貫通して南極Sに至ります。 射影線の通過点
,
が、点Pの対応点になります。 は球面上の点で、は円板上の点です。
つぎに、赤い矢線のように、ポアンカレ円板の西端 W(u = -1) から半球面上の点を通って射線を伸ばすと、上半平面に点Pの対応点
を得ます。
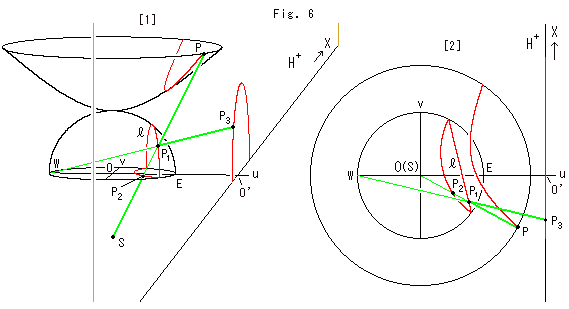
上のFig.6をご覧ください。
赤い曲線は同一の双曲的直線ですが、モデルごとに違った形や大きさで描かれています。 図は、それらの直線が射線でどうむすばれるかを見たものです。 上半平面は、u軸に沿って平行移動させて、点O'に原点をとっています。 上半平面をずらせると、他のモデルの原点Oとは一致しませんが、見やすくなるからです。
[1]: 双曲的直線は見た目には、双曲面上では双曲線、半球面上では垂直に立っている半円
、ポアンカレ円板上では円弧、上半平面上では半円といった具合になっています。 上半平面上の図形は、原点をOからO'へずらせた分だけ大きく描かれています。 しかし、上半平面上では、物差しの目盛りをその分だけ広げて長さを測ることにすれば、実質的な変化は生じません。
緑色の2本の射線が点でつながっています。 点Sと点Wと4つの点P,,,は、同一の平面上にあります。 ということは、その平面上に4点のうちの1つでもあれば、他の3点も同じ平面上にあるのです。 この平面はつねに赤道面に垂直です。 そして、1つの点を動かすと、他の3つの点が一斉に動きます。
[2]: 真上から[1]を見たものです。 点を通っている真直ぐな線は半球面上の半円です。 それは半球面を垂直な平面で切った切り口になっています。
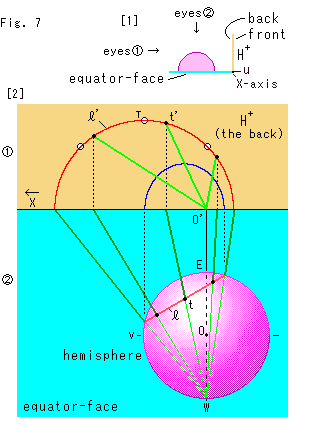
Fig.7をご覧ください。
図とうものは、私たちの理解をおおいにたすけます。 しかし、ときには図にだまされることがあります。 Fig.6では、点が半円の頂上にあるときは、点はいつも上半平面上の半円の頂上にあるように見えます。 ところが、実際はそうではないのです。
[1]: 見ようとするものの配置です。 ピンク色の半球面が水色の赤道面の上にあって、黄色い上半平面が右側に立っています。 私たちは、視線(our eys)
と
の方向から観察します。
[2]: 上の方のは上半平面で、視線で見ています。 下の方のは赤道面とその上の半球面です。
視線の上半平面では：
見ているのは上半平面の裏側で、X軸の正の向きが左側になっています。 緑色の線は点Wから出ている射線です。 赤い半円
は双曲的直線で、半円に対応しています。 半円上の3つの黒いスポットは、半円上の黒いスポットの点が移されたもので、点t'は点tに対応しています。 
印しは頂上Tと、そこから左右に45
にとったところの点です。 青い曲線は、半円を平行射影したもので、半円ではなく半だ円になっています。
視線の半球面上では：
赤い線は、双曲的直線で、赤道面に直立している半円です。 その上の3つの黒いスポットは、頂上tと、そこから45にとった2点です。 点Wからの射線が赤い直線のところで色に濃淡が変わっているのは、そこで射線が半球面を貫通して外へ出るのを表わしています。
射線によって半円が半円に移るわけですが、それらの頂上と頂上は対応していません。 半円の頂上tは、半円の頂上Tになるのではなく、そこからずれた点t'になるのです。 印しの点と黒いスポットの点が一致するのは、半円の面が上半平面と平行になるときだけです。 そのとき、4つの点P,,,がu軸を通る垂直な平面上にあります。
目で見てそれとわかる特徴的な点、たとえば三角形の頂点などだけに注目するときは、上のようなことに気をつかう必要はありません。 しかし、曲線や曲面がなめらかなところでの点と点の対応には注意してください。
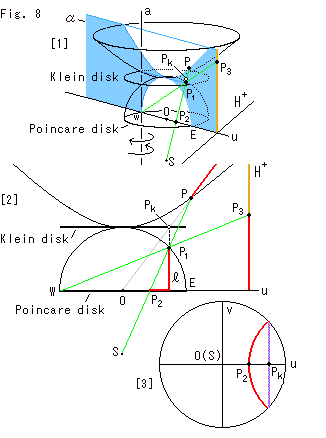
Fig.8をご覧ください。
双曲面と半球面にはさまれているクライン円板(Klein disk)も含めて、5つのモデルを3本の射線で一つに描きます。
[1]: 各モデル上の図形を省いて、5つの対応点(P,,,とクライン円板上の点
)だけを見ています。 平面
には5つの対応点が乗っています。 対応点が前後に動くと、それにつれて平面は、点Wを通る垂直な直線aを軸として回転します。 いま平面がちょうどu軸を通る位置にあります。
[2]: 平面を正面に置いて、上半平面と平行に見ています。 これで見やすくなりました。 赤い線はすべて双曲的直線ですが、どれも真直ぐな線に見えています。 原点Oから右上へのびている灰色の線は、クラインの円板を貫通する射線です。 これはまた、原点Oを通って双曲面を切る平面の断面も表わしています。 その平面と双曲面の交線が点Pを通る赤い曲線です。 そして、射線OPがクラインの円板を貫通する点は、点Pの対応点であって、その真下に点があります。 つまり、点から射線を下ろして半球面に当たったところが、点になるわけです。
平面がu軸上にないときは、図はすこし違ったものになりますが、対応点どうしの関係はかわりません。
[3]: 真上から見ると、ポアンカレ円板とクライン円板は重なっています。 点を通っている紫色の弦がクライン円板上の双曲的直線で、点を通っている赤い円弧がポアンカレ円板上の双曲的直線です。
一つのモデルから他のモデルへ移るのに、点や点で射線の乗り換えをしなければならない場合がありますが、これで5つのモデルがむすびつけられました。
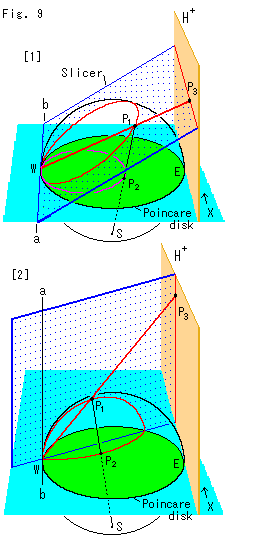
Fig.9をご覧ください。
半球面を切るスライサー(Slicer)と名付けた平面を前に使いました。 そのスライサーをつかって、上半平面上の曲線が見た目に水平や垂直になる特別な場合を見てみます。
[1]: ヒンジ軸abは、ポアンカレ円板に点W(u = -1)で接しています。 そのヒンジ軸abと平行に上半平面が立っています。 そしてスライサーは、半球面を切って円形の切り口をつくると同時に、上半平面を水平な直線に切ります。 点が半球面の切口の円に沿って動くと、点Wから出ている赤い射線によって点は水平に動きます。 また、南極Sから出ている黒い射線によってポアンカレ円板上の点は円を描きます。 このとき、半球面上の円もポアンカレ円板上の円も点Wを通っているように見えます。
上半平面上の水平な線は、X軸上に中心をもつ半円ではないので、ふつうの双曲的直線ではありません。 しかし、ホロサイクルですから、半径無限大の円とみることができます。 一方、半球面やポアンカレ円板上の双曲的直線の両端は、点Wでループになってつながっているように見えます。 そうすると、上半平面上の水平な線も点Wに相当するどこかでつながっいるように思えます。
[2]: ヒンジ軸abが点Wを縦に通るようにして、スライサーをポアンカレ円板に垂直に立てます。 このスライサーは、Fig.8の平面と同じです。 スライサーは、半球面を切って半円形の切り口をつくり、上半平面を垂直に切ります。 そして、点が半球面上の半円に沿って動くと、点は垂直に動きます。 一方、ポアンカレ円板上の点は円弧を描きます。 (クライン円板の場合の双曲的直線は、スライサーと円板の交線になります｡) このとき、半球面上の半円とポアンカレ円板上の円弧の一端が、ともに点Wを通っているように見えます。 これは、上半平面上で半直線として表わされていることに符合します。
半球面上や円板上の双曲的直線をA、それに対応する上半平面上の双曲的直線をBとすると、
Aの両端が点Wを通るように見えるときは、Bは水平な直線
Aの一端だけが点Wを通るように見えるときは、Bは垂直な直線
となっています。
それでは、点が点Wの方へ近づいていったときは、どうなるのでしようか？ これは、どのモデルも開空間あることを想い起こすことで解決します。 点も点もけっして点Wに達することはありません。 また、点はけっしてX軸に達することはありません。 ですから、赤い射線 W-- は、垂直や水平にいくらでも近づけますが、垂直にも水平にもなってしまうことはないのです。
ポアンカレ円板との関係をとりあげましたが、クライン円板でも点と点の動きは同じです。 クライン円板上では、ポアンカレ円板上の円がだ円に、円弧が直線に変わるだけです。
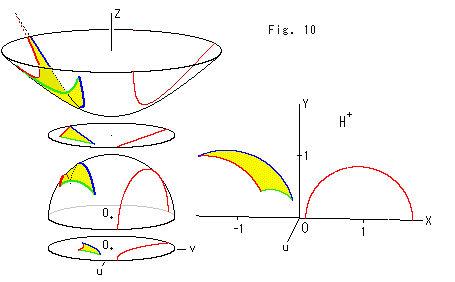
Fig.10をご覧ください。
1つの三角形と直線が形を変えて5つのモデルに描かれています。 直線はすべて双曲的な同じ場所に描かれています。 見やすくするために、各モデルを離していますが、上半平面以外はZ軸を共有しています。 上半平面は原点Oに立っていたものです。 そのY軸は、左側のZ軸と重なるものです。 上半平面を正面から見る方向に合わせてu軸をこちらの方へ向けています。
これで、5つのモデル間を行き来することが、自在にイメージできるようになりました。