第２部 双曲的非ユークリッドの世界

Ch.24 曲率 (1)

      計量は用いるモデルごとにちがうので、双曲的非ユークリッドの世界であることを特徴づけるには不便です。 計量とか重みというのは、わざとつけた感じがしますね。
曲率がわかれば、モデルがなんであっても、双曲的非ユークリッドの世界であるのかないのかを直ぐにいうことができます。 計量は式で表わされますが、曲率は一つの定数ですので、とても便利です。 ここでの曲率は、ガウスの曲率とよばれているものです。
      曲率とは、ものの曲がり具合です。 そして、いたるところが一定の曲率で、それがゼロならユークリッドの世界、正なら楕円的非ユークリッドの世界、負なら双曲的非ユークリッドの世界だといわれています。 平面でも空間でもどんな次元でも、曲率だけで決まるのです。 曲率が0でない空間が、曲がった空間です。 計算の便のために、0でない曲率は、1 か -1 にとります。 (定曲率の値を変えることは、あとでやってみます｡)
曲率が一定なものは、何処でも歪み方が同じで、等質といわれています。 曲率が一定な空間では、長さも角も変えない(等長変換)で図形をどこへでもっていくことができます。

     「曲率が負であるものこそ双曲幾何をもっているのだ」と最初に指摘したのはベルトラミーです。 Ch.18で、ベルトラミーの擬球の上が双曲的非ユークリッドの世界(平面)になっているのを見ました。 擬球の曲率は -1となっているはずです。 ここでは、そのことを調べてみます。

      物理的には、ポアンカレやクラインの円板は円板であり、上半平面は平面です。 ですから、それらの曲率は、計量が与えられていることから計算しなければなりません。 ところが幸いにも、擬球の曲率は、ふつうの曲面として、そのままの形で計算できます。 といっても、計算は微分幾何によるいささか面倒なものです。 私なんか、計算途中で何をしているのか分からなくなったりします。 そこで、考えやすい接触円(osculating circle)や接触球(osculating ball)というものを使って、順を追ってすすめます。

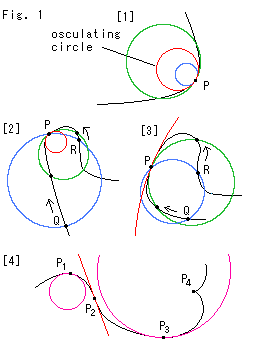
      Fig.1をご覧ください。
      [1]: 曲線に円を当てて接触円を定めようとしているところです。 接触点Pの近くでは、曲線は捻れていなくて滑らかだとします。 接触円は、曲線と(点でなく線で)接触する最大の円です。 つまり、曲線をさまざまな大きさの円弧が連なったものとみて、点Pでそんな円弧と最大限に重なる円が接触円です。 図では、中央の赤い円がそれで、丁度はまっています。 緑色の円は大きすぎ、青い円は小さすぎます。
      [2]: 点Pでの接触円をつかむ正確な方法です。 点Pを挟んで曲線上に2点Q,Rをとります。 3点P,Q,Rから1つの円がきまります。 点Qと点Rを点Pの方へ動かします。 いま、青色の円が緑色の円になっています。 つづけて点Q,Rを動かしていったとき、3点P,Q,Rで定まる円が、ある一定の円に限りなく近づくなら、その円が接触円になります。 赤い円が接触円です。
      [3]: [2]と同じ方法ですが、2点Q,Rを点Pの方へ動かすにつれて、3点P,Q,Rで定まる円が大きくなっていくときの様子です。
      [4]: 3点,,における接触円です。 点は変曲点ですので、“ある一定の円”が見出せません。 しかし、半径無限大の接触円も受け入れることにすれば、接線が接触円になります。 点では、黒い曲線と赤い接触円が交差しているように見えます。 しかし、“ある一定の円”が見出されるので、ちゃんと接触円が得られています。 点では、“ある一定の円”も定まった接線もありませんので、接触円はありません。

      接触円の半径(曲率半径)がrのところの曲率Kは、

です。 変曲点や直線になっているところでは、接触円の半径rが無限大になるので、曲率Kはゼロです。

      曲面のある点の近傍が球冠状とよばれる形になっていると、その点の曲面の曲率を接触球を使って得ることができます。 そのような点をヘソ点といいます。 接触球は、接触円と同様な考え方のもので、くぼみに(点や線でなく面で)接触する最大の球です。
      接触球が半径rのところでの曲面の曲率Kは、

です。 単位半径の球面の曲率Kは1です。 ふつうの平面は、接触球の半径が無限大になりますから、その曲率Kは0です。

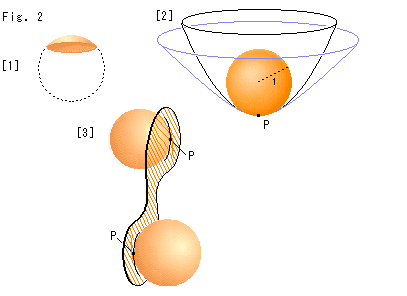
      Fig.2をご覧ください。
      [1]: 球面を平面で切った球冠です。 球冠上の点はすべてヘソ点です。
      [2]: 回転双曲面の中に回転放物面を入れ、その底に接触点Pをとって接触球をおいたものです。 図の場合、回転双曲面と回転放物面の両方に接触球が接しています。 接触球の半径は1ですから、2つの回転面の点Pにおける曲率Kはともに1です。 ちょっと見ると、双曲面の曲率の方が放物面の曲率より小さいように思えますが、そうではありません。 曲率は1点Pで見てのことですから。 この曲面は回転面ですので、その母線の曲率をFig.1のように求めて2乗しても同じです。
      [3]: 凹凸になっている曲面のくぼみに接触球をおいたものです。

      曲面のヘソ点でない点の曲率を求めます。
ヘソ点でないときは、2つの接触円をつかって曲率を得ることができます。 なめらかな曲面の点Pにおけるガウス曲率Kは、法線を通る平面で切ってできる曲線(曲面の断面)の最大曲率と最小曲率の積です。 それらを,とすると、

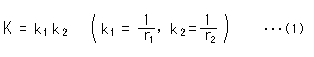
となります。 ,は、接触円,の半径です。
この式は、2つの接触円,が点Pから見て同じ側にある場合です。 ,が点Pを挟んで向かい合っているときは、右辺にマイナス "-" がつき、K < O となります。 法線を通って曲面を切る平面は、その上の曲線の曲率が最大なものと最小なものの2枚があるわけですが、それらは必ず直交します。

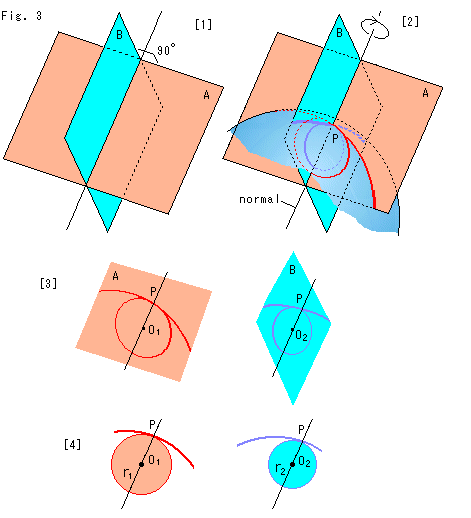
      Fig.3をご覧ください。
最大最小の曲率,を2つの接触円,で求めます。
      [1]: まず、1本の軸に2枚の平面A,Bを直交させて固定したものをつくります。
      [2]: その軸を法線(normal)として点Pに刺します。 すると、平面Aには曲面を切ってできる赤い曲線が得られます。 同様に、平面Bには青い曲線が得られます。 その2曲線のそれぞれに接触円を置きます。 そして、平面A,Bを図のように回転すると、赤と青の曲線は変化します。 それにつれて、2つの接触円の大きさも変化します。
回転中に、1つの接触円が無限大になったり、2つの接触円の大小が入れ替わったりすることがあってもかまいません。 回転をつづけてください。
      [3]: 平面A上の接触円を、平面B上の接触円をとします。 平面Aでは、最大になった接触円を赤い曲線とともに、平面Bでは、最小になった接触円を青い曲線とともに取り出しています。
      [4]は、[3]の各面をこちらに向けて描いたものです。 図のように赤い接触円の半径を、青い接触円の半径をとしています。 これらを上の式(1)に入れれば、曲面の曲率Kが得られるというわけです。

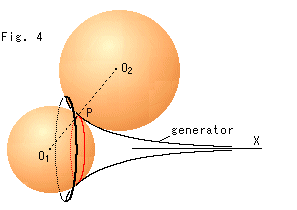
      Fig.4をご覧ください。
ベルトラミーの擬球の曲率を求めます。 擬球は回転面で、その面は鞍形状になっています。 点Pに内側と外側から球を当てたところですが、これらの球は面接触にはなりません。 内側の球が擬球と接しているところは、擬球のX軸に直交した赤い円です。 外側の球が接触しているのは、擬球の母線(generator)です。 ですから、どちら側の球も接触球ではありません。 しかし、このように1点に2つの球(半径)と(半径)を当てることができる場合の曲率は、式(1)にマイナスをつけてものになります。

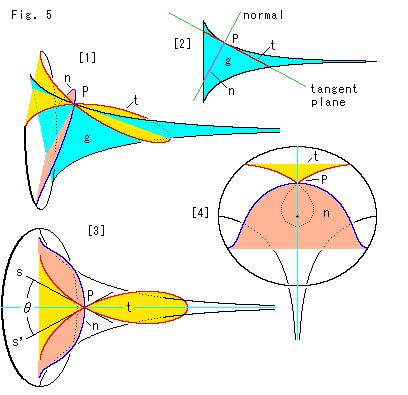
      Fig.5をご覧ください。
球でなく、接触円で考えてみます。 といっても、法線上に中心をとった円が線接触できる範囲は限られています。
      [1]: 面g,n,tは、点Pを通る3つの平面で擬球を切った切口です。 これらの面はたがいに直交しています。 切口の曲線も面と同じ記号で表わすことにします。 水色の面gは、向かい合った母線に囲まれています。 黄色い面tは、点Pを通る接平面です。 面gと茶色の面nの交線は、点Pを通る法線になっています。
      [2]: [1]を真横から見たものです。 右下がりの直線は、接平面(tangent plane)tです。 赤いところが切口tです。 右上がりの直線は、法線(normal)です。 青いところが切口nです。
      [3]: [1]を法線方向から見たものです。 直線s,s'は、切口tの点Pでの接線です。 法線上に中心をとって点Pに接する円は、角の範囲を逸れると、点接触になってしまいます。
      [4]: [1]を接線方向から見たものです。

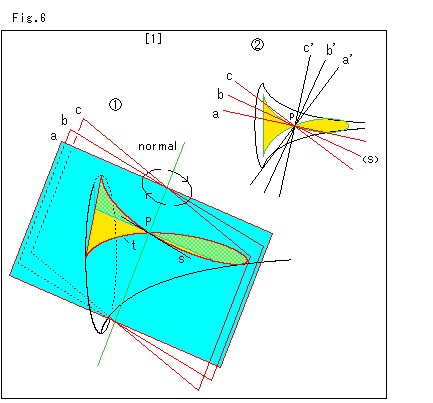
      Fig.6をご覧ください。
もうすこし詳しく見ていきましよう。

      [1]: 点Pを通る法線を共有する平面で擬球を切ります。
      の矢印のように、平面を回転して切っていきます。 平面aだけを水色に塗っています。 黄色いところは、点Pにおける疑球の接平面による切口です。 その縁が赤い曲線tです。 直線sは点Pにおける曲線tの接線です。 平面bが接線sに沿っていて、平面aと平面cがその前後になっています。
      は、法線方向から見たものです。 a',b',c'は、それぞれ平面a,b,cに直交した平面です。

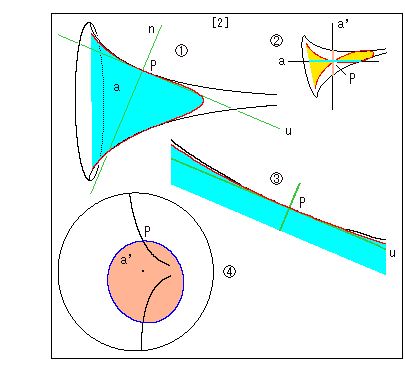
      [2]: 平面a,a'と疑球との関係です。
      は、平面aによる切口を正面に向けたものです。 切口だけを着色しています。 緑色の直線uとnは、それぞれ点Pにおける母線の接線と法線です。
      は、を法線方向から見たものです。 水色の部分が平面aによる切口で、うす茶色の部分が平面a'による切口です。
      は、の点P付近を拡大したものです。 切口の赤い曲線が、母線の曲がりぐあいとならんで凹んでいて、点Pの左右で接線uより上へ行っているのがわかります。 ですから、擬球の外側で平面a上に点Pにおける接触円を得ることができます。
      は、平面a'で切った切口を正面に向けたものです。 切口だけを茶色に染めています。 擬球の内側で平面a'上に点Pにおける接触円を得ることができます。 切口の内部の黒いスポットは、擬球の軸が貫通している点です。

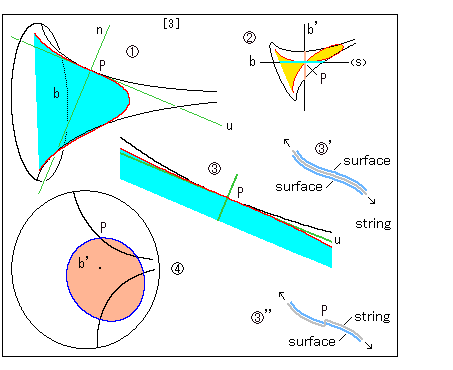
      [3]: 平面b,b'との関係です。 図は上と同じ要領で描かれています。
      を見ると、平面bが接線s ([1]の) を通っています。
      を見ると、赤い曲線が点Pの左側では接線uから上へ伸びており、右側では接線uから下へ伸びています。 つまり、点Pは赤い曲線の変曲点です。 この平面b上では、点Pにおける接触円を得ることはできません。
      これまでに、疑球上の2点をむすぶ直線(測地線)をパソコンで描きました。 ここでは、手にとれる疑球に糸(string)を張って、直線が疑球上をどのように這うかを見て、変曲点の特性を感じ取ることにします。 ところが、糸を疑球の面(surface)から浮き上がらないように張るには、ちょっとした工夫が必要です。 透明な材料で疑球の面をつくります。 本当の面には厚さはありませんが、無視しておきます。
  'は、面を間隙をもった層につくって、その間を通して糸を張ったものです。
  ''は、 糸が面の針穴を通るようにしたものです。 糸が、ある方向に張ったときに面から浮き上がることがなければ、その針穴は糸(直線)上の変曲点です。

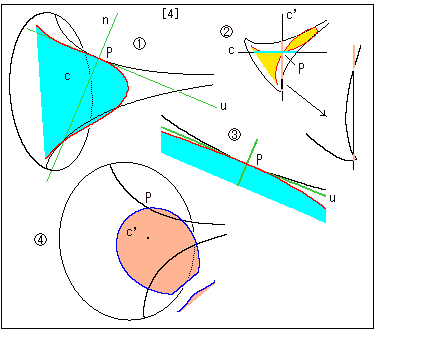
      [4]: 平面c,c'との関係です。 これも上と同じ要領で描かれています。
      の平面c'を点Pから擬球の開口部の方へと見ていくと、平面c'は擬球の外へいったん出て、ふたたび開口部をわずかに切っています。 矢印で示しているのは、その拡大部分です。
      では、赤い曲線が点Pの両側で接線uより下へ伸びたアーチ形になっています。 こうなると、擬球の外側では接触円をまったく得ることができません。
      では、平面c'による切口が途中でち切れています。

      こうして見てくると、擬球の外側の接触円が最小になるのは、母線を含む平面のものに限られることがわかります。 しかし、いまのところ、作図だけではそれ以上のことはつかめません。
そこで、擬球の外側の接触円は母線を含む平面上のものをとることにし、内側の接触円はそれと直交するものをとってみます。

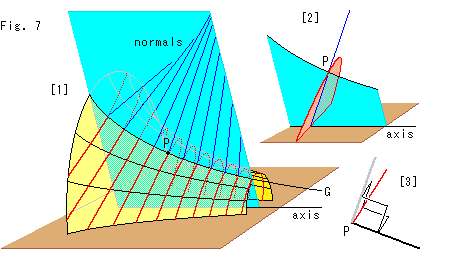
      Fig.7をご覧ください。
      [1]: 茶色い平面に擬球の軸(axis)を横にして置いています。 水色の平面が擬球の母線Gと軸を通っています。 この平面には母線Gの法線(normal)が乗っています。 (擬球の内部の法線は省いています｡)　赤い線は、母線Gと水色の平面の両方に直交した平面と擬球との交線です。
      [2]: [1]から点Pを通る2つの平面による疑球の切口だけを取り出したものです。
      [3]: 点Pにおける2つの切口の接線と法線は、このようにたがいに直交しています。

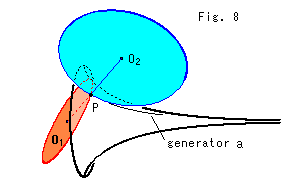
      Fig.8をご覧ください。
2つの接触円,を点Pに置いたところです。 直線 -P- が法線です。

      曲率をつかむには、2つの接触円との半径を知らねばなりません。
擬球の曲率Kはいたるところが一定値の -1 だと言われても、擬球の格好から見て、すぐには肯けませんね。 本当に、そうなっているでしようか。 どこでも？

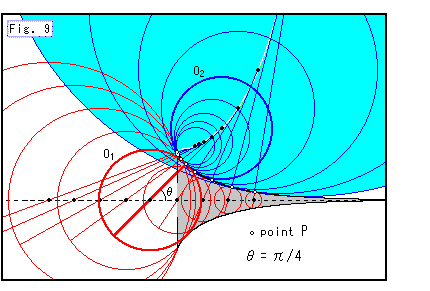
      Fig.9は、点Pの位置を変えていったときの、2つの接触円,の様子を真横から見たものです。
赤い円は擬球の内側の接触円をこちら側に向けて描いています。 どちらの円もFig.4の球の断面だと思ってもかまいません。
母線の曲がりは擬球のしっぽの方へ行くほど緩くなっています。 ですから、点Pをしっぽの方へとっていくと、外側の接触円は大きくなり、内側の接触円は逆に小さくなっていきます。
太く描いた接触円との1組は、ともに半径が丁度1で、法線が擬球の軸となす角が45になっています。
  点Pを開口部の方へ動かすと、外側の接触円は小さくなり、内側の接触円は逆に大きくなります。 しかし、開口部の先端では、どちらの接触円も定まりません。 極限値をとっても、接触円の半径は無限大となり、接触円の半径はゼロとなるので、式(1)をつかうために両者の曲率,を掛けると、

という、わけのわからないものになります。
      これとは逆に点Pがしっぽの方へ行ったときは安心です。 接触円の半径は限りなく小さくなりますが、けっしてゼロにはなりません。 接触円の半径は限りなく大きくなりますが、無限大にはなりません。 しっぽには先端というものがなくて、開かれているからです。
(外側の接触円の中心の白い軌跡はカテナリー(懸垂線)という曲線ですが、それについては後でとりあげます｡)

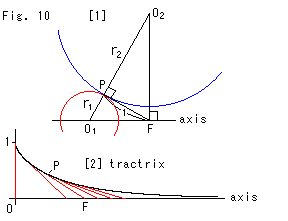
      Fig.10をご覧ください。
さて、疑球の曲率Kを求めます。 疑球を挟んでいる2つの接触円の個々の半径はわからなくても、半径の積がつかめれば足ります。 疑球の曲率は一定ですから、半径の積も一定にちがいありません。
      [1]: 接触円の中心から擬球の軸(axis)に下ろした垂線の足を点Fとして、三角形Fをつくります。 点P,Fをむすぶと、直角三角形FPと直角三角形FPができます。
そして、接触円,の半径をそれぞれ,とすると、

です。 これは、点Pが擬球上のどこにあっても成り立ちます。 この場合、曲面が2つの接触円とにはさまれていますから、擬球の曲率Kは、積の逆数にマイナスがついて、いたるところで K = -1 ということになります。
      [2]: 黒い曲線は擬球の母線(追跡曲線, tractrix)です。 この曲線上の点Pから擬球の軸まで赤い接線PFの長さは、点Pが母線上のどこにあっても一定の1です。 これから見ても、擬球の曲率Kはつねに -1 であることがわかります。 (擬球の曲率を見出すもう一つの巧い方法がありますが、後でふれます｡)

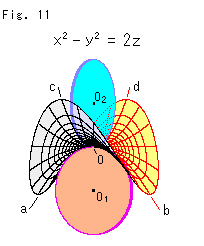
      上の考え方による接触円で曲率の測れる例を見ておきます。

      Fig.11をご覧ください。
鞍形の原点Oに接触円,をあてたところです。 Z軸が,O,を通っています。 谷間の曲線abはYZ平面(x = 0)上にあり、尾根の曲線cdはXZ平面(y = 0)上にあります。
  接触円の半径rですが、曲線abも曲線cdも原点を通るので、簡単に計算できます。 原点を通る曲線の原点における曲率半径rはニュートンの方法

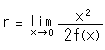
で得られます。 図の鞍形では上下の接触円,の半径はともに1ですので、この鞍形の原点Oにおける曲率Kは K = -1 です。
      擬球とはちがって、この鞍形の曲率Kは一定ではありません。 原点から離れていっても、曲面はずっと波打っていて、曲率は負です。 けれども、原点からすこしでも離れると、急速にゼロに近づきます。 鞍形の縁では、K = -0.1 になっています。

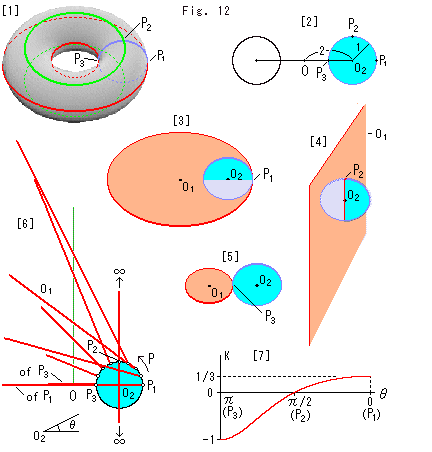
      Fig.12をご覧ください。
      [1]: ドーナツ形の曲面で、トーラスとよばれているものです。 青い円は、3つの点,,を通って、トーラスのチューブを垂直に切っています。 トーラスは地球ではありませんが、この円は子午線とよばれています。
点を通っている赤い円は一番外側の円です。 外側円とよんでおきます。
点を通っている緑色の円は、チューブの一番上の尾根に相当するところです。 その真下の点線の円はチューブの一番下の谷間をめぐっています。
点を通っているもう一つの赤い円は、一番内側の円です。 内側円とよんでおきます。
      [2]: トーラスを中心O(原点)で切った断面です。 トーラスのチューブの半径を1、チューブの中心を通る円の半径を2にとっています。 内側円の半径は1、外側円の半径は3です。 水色に染めてあるのは、チューブ内の接触円です。
      [3]: 点において、チューブの内側で直交している接触円,です。 赤い接触円は外側円です。 点における曲率Kは、K = 1/3 です。
      [4]: 点では、赤い接触円の半径は無限大です。 点における曲率Kは、K = 0 です。
      [5]: 点でトーラスの面を挟んでいる接触円,です。 赤い接触円は内側円です。 点における曲率Kは、K = -1 です。
      [6]: 水色の接触円を正面に置いて、接触点Pを点から点まで連続的に動かしたときの赤い接触円が変化する様子を見たものです。 接触円は断面(直径)が描かれています。 緑色の線は接触円の中心の軌跡です。 トーラスの中心Oを通る垂線になっています。 こんな直線になるとは、意外ですね。
      [7]: [6]のときの曲率Kが変化する様子です。 点 ( = 0)から出発すると、曲率Kは 1/3 からしだいに小さくなり、点でゼロ、 ( = )で -1 になっています。

      曲面の曲率を求めることとは逆に、曲率の方が変わったときは、曲面の形はどうなるでしようか？ 曲率が -1 であれば、なぜ双曲的なのでしようか？ 角と距離が依存し合うことと曲率は、どうつながっているのでしようか？ また、空間そのものの曲率を捉えるには、どうすればよいでしようか？ これらについても、おいおい当たっていくことにします。