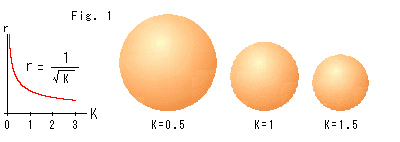
曲率が変わると、擬球の形はどうなるでしようか。 曲率がいたるところ一定なものは、大きさが変わっても、形はもとのままのはずです。 確かめてみます。
Fig.1は、球面の半径rと曲率Kの関係です。 曲率Kが小さくなれば、球面は急激に大きくなります。 当然ですね。
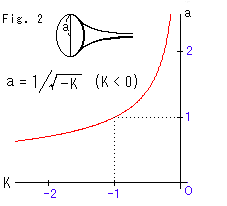
Fig.2のように、擬球に曲率Kを与えると、その開口部の半径aが定まります。 このとき、トラクトリクス(擬球の母線)は
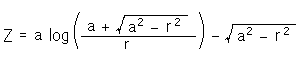
です。
この式だけを見ていると、大きさだけが変わるようには、ちょっと感じられませんね。
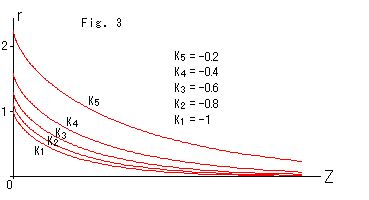
Fig.3は、曲率Kによってトラクトリクスが変わる様子です。 曲率Kをゼロの方へ近づけると、擬球は急激に大きくなります。 (これにともなって、擬球に対応した円板モデルの描画半径も急激に大きくなります。)
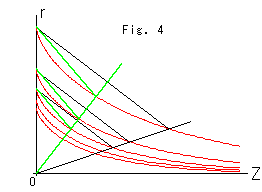
Fig.4は、トラクトリクスが、大きくなっても、形を変えないことを確かめたものです。 原点Oを通る任意の直線を引いて図のように交点を直線で結ぶと、相似三角形ができます。 これで曲線の形がすべて同じであることが分かります。 そして、擬球の形は曲率Kの如何によらず変わりません。
ユークリッドの世界では、曲率Kはゼロです。 擬球の曲率Kをゼロにまでしてしまうと、どうなるでしようか? 上の話からすると、擬球は、もとの形のままで無限に大きくなっているのでしようか。 そうです。 そうでありながら、擬球の面は平面になっているのです。 そして、それがユークリッド平面です!
そして、対応する円板モデルの半径は無限大となり、ユークリッド平面になります。
曲率Kをいくらゼロに近づけても、ゼロでないかぎりは、純然たる双曲的非ユークリッドの世界のままで、擬球の形も変わりません。 あるいは、擬球の大きさにつれて物差しの目盛りを大きくすれば、擬球の曲率Kはつねに -1 であるともいえます。 ですから、正規化にもどって、双曲的非ユークリッドの世界の曲率Kは K = -1 であると固定してもよいわけです。 具体的には、疑球のスカートの裾の半径rを長さの単位にとる約束をすることです。