微分幾何も接触円も使わずに、擬球の曲率を得る巧い手があります。
ガウス-ボンネの定理とよばれている
を利用すれば、面積Aとオイラー数
(カイ)から、曲率Kがすぐに出ます。 面積Aと曲率Kの積KAを全曲率といいます。 (オイラー数はオイラー標数と同じことです。)
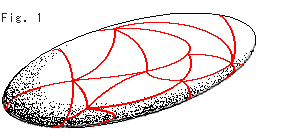
この公式は閉曲面(境界のない、球面やトーラスなど)に適用されるものです。 オイラー数を求めるには、まず曲面全体に三角形や四角形を敷き詰めます。 たとえば、Fig.1のように。 このようにすることを胞体分割とか三角形分割といいます。 そして、その頂点と辺と面の数をかぞえます。 頂点というのは、線分が集まった交点を指します。 その2頂点をむすんでいる線分を辺とよんでいます。 そんな線分で囲まれているところが面です。“分割”とよんでいるのは、三角形や四角形を敷き詰めた結果が分割したものになっているということです。
オイラー数を求めるには、曲面上に三角形や四角形を具体的に描く必要はありません。 頂点と辺と面の数さえわかれば、
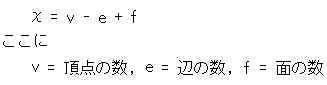
と算出されます。 この公式は、0次元(頂点)、1次元(辺)、2次元(面)と並んでいるので、すぐに覚えられます。
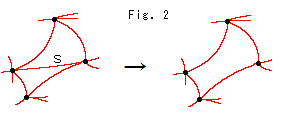
Fig.2をご覧ください。
図のようになところでは、辺sを省いてもかまいません。 辺を1つ取り去れば面の数も1つ減り、オイラー数に変わりはないからです。 (面だけを取ると穴があいてしまいます。) Fig.1の三角形は多すぎるのです。
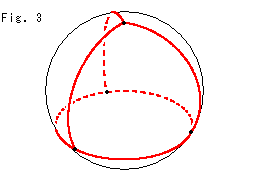
Fig.3のように、トポロジー的に球や四面体とみなせるものなら、4つの三角形で足ります。
オイラー数は
= 4 - 6 + 4 = 2
です。
球の半径をrとすると、その曲率Kは 1/
で、面積Aは 4
ですから、全曲率KAは球の大小に関係なく 4 です。 これを式(1)に当てはめると、オイラー数が2であることと一致します。
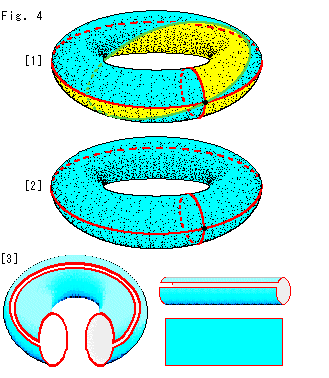
Fig.4をご覧ください。
トーラスではどうでしようか。
[1]: 三角形2枚で覆いつくすことができます。 この場合、オイラー数は 1 - 3 + 2 = 0 で、ゼロです。
[2]: 1辺を省いて、1つの面で覆ったものです。 図では緑色の辺を除きましたが、縦の赤い辺(小さい円)も穴をくぐっているので、それを取り去ってもかまいません。 オイラー数に変化はなく、 1 - 2 + 1 = 0 で、やはりゼロです。
[3]: [2]の面を赤い線に沿って切り開いて広げてみると、このように四角形でトーラスが包まれていたことがわかります。 そして、オイラー数は 0 - 1 + 1 = 0 と計算できます。
トーラスの全曲率は、すぐ後で見ます。 切ったり貼ったりすることについては、後の方の章でまた取り上げます。
さて、擬球の曲率Kは -1 で一定だとわかっています。 このKをガウス-ボンネの公式から求めてみましよう。 いや、まってください。 擬球には、境界がありますし、無限に伸びている尖った尻尾(カスプ)がついています。 そんなものには、ガウス-ボンネの公式は適用できません。
ところが幸いにも、巧妙な手があるのです。
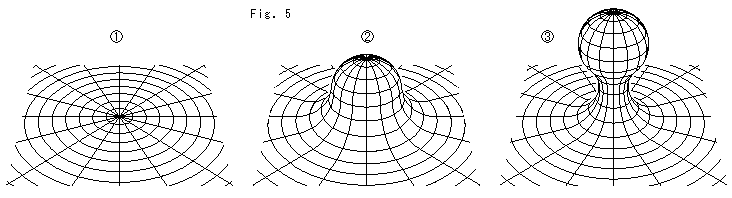
Fig.5をご覧ください。
無限に広い平らな台の上にやわらかい面を置きます。 そのままですと、平面
になっています。 
は、それを下から突き上げたものです。 
は、さらに突き上げたものです。 の形になっているものを押さえていくと、からの平面へともどります。
平面の曲率はいたるところでゼロですが、それが歪められたやの形のものでは、曲率は各点で異なっています。 そのような曲がった面の全曲率は積分で表されて、ガウス-ボンネの公式は
といったものになります。 しかし、心配いりません。 境界がない曲面の全曲率は、その曲面をどのように歪めても、はじめと変わらないということを利用すれば、複雑な積分をしなくてすむのです。 膨れたところをつくれば必ず凹んだところができます。 歪めるといっても、滑らかなものに限ります。 アイロンをかけて、皺をなくすようなことは論外です。 そうして新しくできた正曲率のところと負曲率のところは全体として相殺されます。 ですから、やは平面ではありませんが、その全曲率はゼロです。
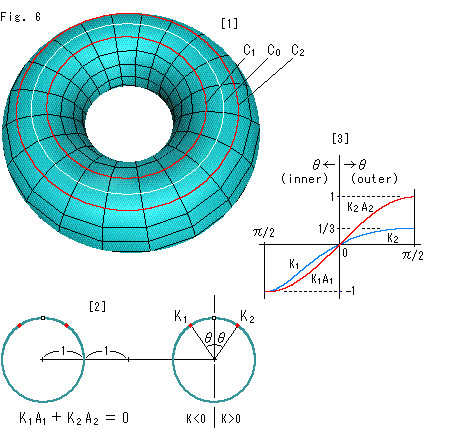
Fig.6をご覧ください。
正負の曲率が相殺される好例をトーラスで見てみます。 計算の便のために格好のよいトーラスをとりますが、不恰好でもリクツは同じです。
[1]: 白い円
はトーラスのチューブの一番上を通っています。 2つの赤い円
,
は、白い円から等距離のところにあります。 このような円が集まってトーラスをつくっていると考えます。
[2]: トーラスの断面です。 
,
は、それぞれ円,上の1点における曲率です。 曲率に円の長さ(1次元の面積)
を掛けたは、円上の全曲率です。 同様に、
は円上の全曲率です。 そして、
が成り立ちます。 この関係は、角
の大きさがどんなであっても変わりません。
[3]: 青い曲線は、トーラス上の1点における曲率,と角との関係です。 内側の端では -1、外側の端では 1/3 となっています。 赤い曲線は、円,上の全曲率 , と角の関係です。 (作図の都合で、赤い曲線は上下を定数2で割っています。) 赤い曲線はサインカーブになっていて、青い曲線とはちがって、左右の絶対値が同じです。
これらのことから、トーラスの(全体の)全曲率は、内側(負曲率)と外側(正曲率)がキャンセルしあって、ゼロであることがわかります。 トーラスは平面を変形したものではありません。 もとから曲がった面です。 けれども、全曲率はゼロなのです。 そして、式(1')の右辺からオイラー数もゼロであることが知れました。 積分も三角形分割もせずに済みました。
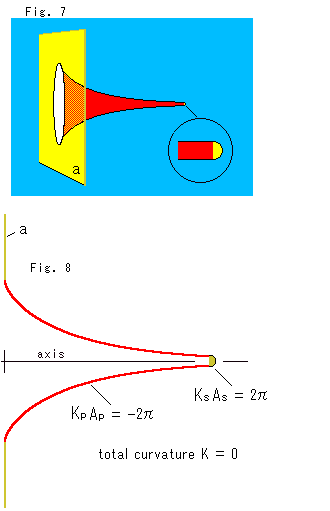
Fig.7をご覧ください。
それでは、擬球の曲率を求めましよう。 Fig.5を真似るのですが、むろん、疑球自体を変形するのではありません。
まず、赤い擬球が細くなって、半径が変化しないとみなせるウンと先の方で尻尾を切ります。 そして、図のように、切り口を黄色い半球で蓋をします。 まるで囲んであるのは拡大図です。 つぎに、擬球のスカートのところに開口部と同じ大きさの穴がある黄色い平面aを当てます。
半球(半径
)の曲率 
は 1/
で、面積 
は 2
ですから、黄色い半球の全曲率 は半球の大きさに関係なく 2 です。
切り落とされた尻尾の面積は、無限遠まで伸びていますけれど、極わずかです。 それで、擬球の面積
は、尻尾が無限遠まで伸びのたままの 2 だとします。 すると、擬球の曲率を
と表すと、その全曲率 は 2 と書けます。
Fig.8をご覧ください。
擬球の軸(axis)を通る平面で切ったFig.7の断面です。 全体の全曲率(total curvature)は、Fig.5の考えで、ゼロですから、
] + [半球の全曲率2] = 0
つまり、
+ 2 = 0
です。
したがって、擬球の曲率は = -1 と得られます。 そして、オイラー数も = -1 とつまめます。
ここで、ちょっと注意しておいてください。
この話しは、擬球の曲率がどこでも一定であると分かっていてのことです。 また、擬球の曲率を見出した過程では、式(1)そのものをつかわずに、それを支えている「正負の曲率は相殺される」ということだけに頼っています。 さらに、胞体分割をすることなく、オイラー数を得ています。
平面aは、その全曲率はゼロなので、計算上ではあってもなくたもよいのです。 しかし、Fig.5の考え方によって、事が成り立っているのがキーになっています。
もう一つ。 本当の擬球の尻尾の先は閉じていません。 キャップをかぶった擬球は本物ではありません。 それでいて、真の擬球の正確な曲率が得られたのです。
ところで、平面aのかわりに半球のようなものでふさぐことを考えてはなりません。 そんなことをすれば、尻尾の方の半球とあわせて、全体がトポロジー的に球と同じものになってしまいます。
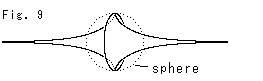
Fig.10は、2つの擬球と球を重ねたものです。 擬球2つ分の面積と体積は、点線の球(sphere)の面積4
と体積
に正確に一致しています。 なにか仕掛けがあるのかも知れません。