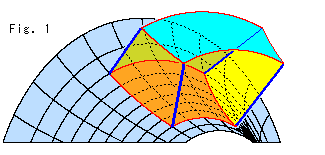
Fig.1は、ウンと大きな擬球をつくって、小屋を建ててみたものです。 柱が傾いているように見えますが、ちゃんと法線方向に立っています。 空色の屋根は双曲的水平(鞍形)です。 この小屋に住んでみるのは、まことに興にのったものといえるでしよう。 双曲的な格好のベッドやテーブル持ち込んで。 でも、各点での重力の方向も法線方向でないと困ります。
宇宙船に乗って地球を見下ろします。 そして、地上にもどると、眺めた丸い地球を見失います。 双曲的非ユークリッドの世界についても、図のような小屋に住んでしまうと、かえって世界が見えません。 一方、擬球やこれまでのモデルから双曲的非ユークリッドの世界を察するには、相当な空想力を費やさねばなりません。
双曲平面は四方八方が等質です。 けれども、擬球は偏った格好をしているので、つい、歪な空間の中のものに感じてしまいます。 これから作る紙細工は、四方八方がまったく同じです。 作られた面を平面だと思いさえすれば、100%実際の双曲平面です。 手で触れることができると同時に、その世界のどこにいるかを知ることができるものです。
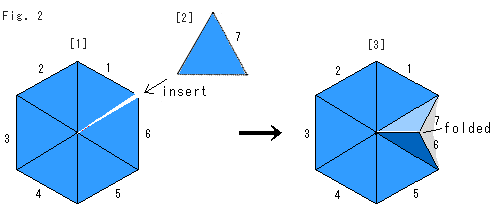
上のFig.2をご覧ください。 すこし厚つ手の紙を正三角形に切ります。 すくなくも50個以上切るとよいでしょう。 はじめに[1]のように、6個の三角形を切れ目を１つ残してテープでゆるくつなぎます。 その切れ目に[2]のもう1つの三角形を無理に差し込んでゆるくテープでとめると、つぎ目で折れます(folded)が、[3]のような七角形ができます。 テープ留めをゆるくするのは、どのつなぎ目も折れるようにして、ジグザグでも七角形にするためです。
Fig.3は、こうしてできた七角形の実物写真です。 ご覧のように、歪に波打っています。 奇数枚の三角形が1点を共有しているので、きれいなジグザグにはなっていません。
この歪んだ七角形の周囲に三角形をつぎ足していきます。 ただし、どの頂点にも、それを共有頂点として、7個の三角形が集まるようにします。 平面をつくっているのですから、輪にららないように注意してください。１個ずつつないで、できている平面の縁を広げていくようにするのです。
Fig.4は、三角形を少しつぎ足していった写真です。 この双曲平面は、ヘナヘナになっています。 三角形の裏側すら見えています。 ですけれども、どの頂点も特別ではありません。 どこも公平で、平面の中心を見出すことはできません。
紙細工はヘナヘナですが、それを平面とみて、一つ一つの三角形の上を小さな虫になって這っていきます。 Ch.4の絵と見比べてください。
阿原一志が、3つの角が54
,63,63の二等辺三角形を使った素晴らしいプログラム ハイプレインをつくっています(浮き輪の穴も作れます)。
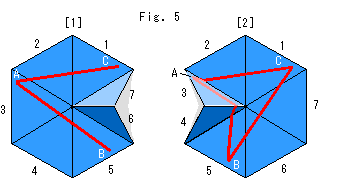
Fig.5をご覧下さい。 紙細工の双曲平面に三角形ABCを描きます。 図はFig.3の歪んだ七角形の上に描く例ですが、大きな三角形を描くときは、Fig.4のような十分大きい紙細工を先に作ってから行ってください。
[1]は、紙細工の三角形1〜5を平坦にして、赤い辺ABと辺ACを引いたところです。
[2]は、紙細工の三角形1,2と5〜7を平坦にして、残りの赤い辺BCを引いて三角形ABCにしたところです。
描いた三角形ABCの角と辺の長さは、[1],[2]のようにして、ふつうに測ります。 ご覧のように、測るまでもなく内角の和は
より小です。
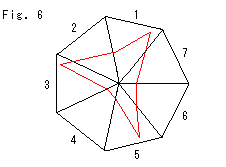
Fig.6は、歪んだ正七角形を無理やりに押さえつけて(あるいは、円周方向に圧縮して)、平坦な正七角形にしてみたものです。 赤い折れ線は、その上に描かれてあった三角形ABCです。 ポアンカレ円板上の三角形に見えるではありませんか。 当然、長さも角もFig.5とは一致しませんが、双曲的平面の定性的な性質がよくわかります。
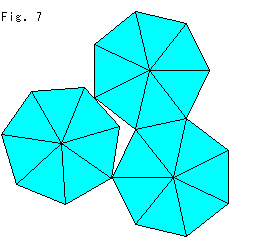
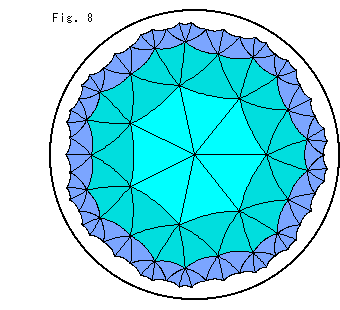
Fig.7のように、この平坦な正七角形で平面を敷き詰めようとしても、どうしても隙間ができてしまいます。 そのため、自由に図形を描くことができません。 しかし、すでに承知しているように、双曲平面でなら敷き詰め可能です。
右のFig.8は、ポアンカレ円板上の正三角形のタイル張り(参照 Ch.12)です。 111個の正三角形が描かれています。 ポアンカレ円板上のすべての正三角形は、おおよそ
辺 = 1.124 (双曲的長さ)
内角 = 2/7 = 0.8976 rad = 51.43
となっています。
三角形をリング状に色分けしています。 このような輪の原点から外側までの双曲距離は、大雑把に言って 1,2,3,,,になっています。
このタイル張りを思いながら、紙細工の上を辿って行けば、双曲平面をかなり実感できます。