だ円的非ユークリッドの世界に関しては、ユークリッドの世界と行き交う巧いツールがあります (参照 Ch.1)。 しかし、双曲的非ユークリッドの世界につては、そんなツールがありません。 むろん、ユークリッドの世界の点と双曲的非ユークリッドの世界の点を対応させることはできません。 とはいえ、二つの世界を対比できないかと工夫してみました。 三角形でそれを見てみます。
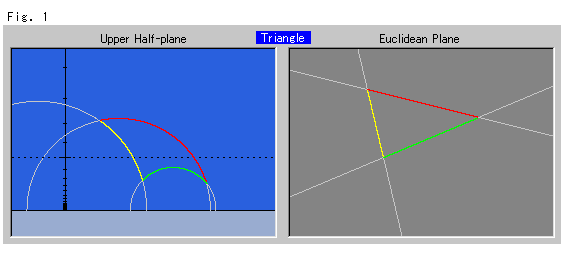
Fig.1をご覧ください。
左側の青い平面が上半平面
で、右側のうす黒い平面がはユークリッド平面です。 三角形の同色の辺を対応させて、上半平面上の双曲的長さとユークリッド平面上のユークリッド的長さを等しくしています。
灰色の線は、観察の便のために描いてあるだけです。 上半平面の黒い点線はY軸の目盛りの基準値を示しています。 そのY軸は、観察用のもので、どこにあってもかまいません。 同じ三角形でも、上半平面上では、上の方に描くと見た目に大きくなります。
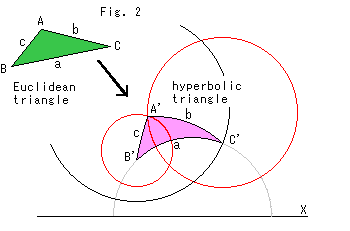
Fig.2は、ユークリッド平面上の三角形を上半平面上に作図で移す例です。
簡単のために、上半平面上の三角形を双曲三角形(hyperbolic triangle)、ユークリッド平面上の三角形をユークリッド三角形(Euclidean triangle)とよぶことにします。
緑色の三角形ABCがユークリッド三角形で、ピンク色の三角形A'B'C'が双曲三角形です。 その変換は、長さだけを両世界で等しくして、角はそれぞれの世界のルールにゆだねることにします。 どちらの世界でも、3辺を与えれば角の方は自動的にきまるからです。
三角形を移す要領は、ユークリッド平面上でコンパスをつかってするのと同じです。 違うのは、円の中心が上の方へずれることだけです。
まず、辺B'C'を乗せるX軸上の半円(双曲的直線)を適当に描き、その上の好みのところに頂点B'をとります。 そして、点B'を双曲的中心として、双曲的半径A'B'(= AB)の赤い双曲的円と双曲的半径B'C'の黒い円を描きます。 黒い円と半円との交点の1つをとり頂点C'にします。 つぎに、点C'を双曲的中心とする双曲的半径A'C'のもう一つの赤い円を描きます。 2つの赤い円の交点の1つを頂点A'にします。 3点A',B',C'を双曲的直線でむすぶと、上半平面上のピンク色の三角形A'B'C'になります。
逆に、双曲三角形をユークリッド三角形に移すときは、3辺の双曲的長さだけをそのままユークリッド的長さとして描けばよいのです。
こうして三角形を異なる世界へ移しあえるわけですが、三角形ABCと三角形A'B'C'を合同だとすぐにはいえません。 合同条件が定められていないからです。
下のFig.3は、ユークリッド三角形を上半平面に移すときに、移す頂点の位置を変えてみたものです。 移された双曲三角形は見た目に異なりますが、すべて合同です。 双曲三角形の内角はユークリッド三角形のそれより小さくなっているのですが、目立ちませんね。 それは、ユークリッド三角形が比較的に小さいからです。
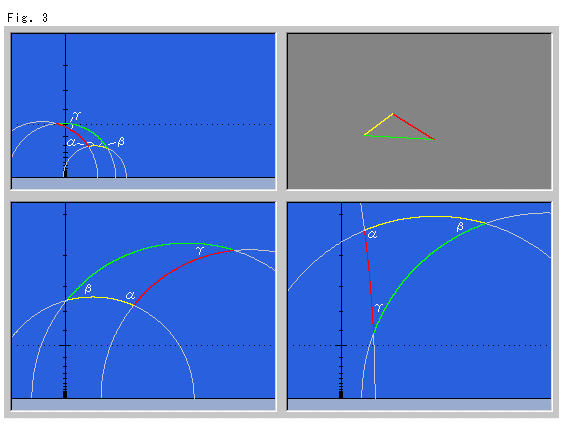
Fig.4では、ユークリッド三角形をすこし大きくして直角三角形にしました。 双曲三角形とユークリッド三角形の角の差異が、はっきり見て取れます。 たしかに、双曲三角形の内角は、小さくなっています。
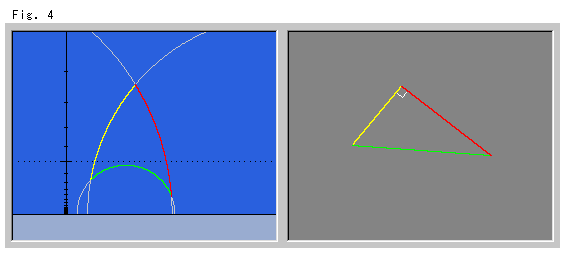
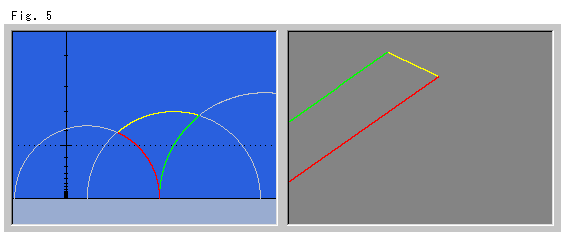
つぎのFig.5は、三角形の頂点の1つが無限遠のときです。 ユークリッド平面では、無限遠の頂点をもつ赤と緑の半直線が平行に描かれています。 こんなものは、三角形とはいえません。 それが双曲的非ユークリッドの世界では、三角形になるのです。 その頂点の1つがX軸に達しており、そこでの内角は当然ゼロでいます。 そして他の2つの内角の和が、180
より小さいことが一見してわかります。
こんどは、平行線です。
双曲的非ユークリッドの世界では、基線に関して、その上にない1点を通る平行線は2本あり、平行線と等距離線は別物です。 そこで、描画のために次のようにすることにします。 簡単のために、上半平面上の平行線を双曲平行線、ユークリッド平面上の平行線をユークリッド平行線とよんでおきます。
双曲平行線からユークリッド平行線へ：
2本の双曲平行線の交点から基線までの距離を、ユークリッド平行線間の距離
とする。 ユークリッド平面で、その距離を基線のどちら側にとるかはオプシ
ョンとする。
ユークリッド平行線から双曲平行線へ：
まず、上半平面上に、ユークリッド平面上の平行線間の距離を等距離とする
等距離線を描く。 その等距離線上の1点をオプショナルに選んで、2本の双曲
平行線を通す。 (その1点で2本の双曲平行線と等距離線が交わります｡)
いずれの場合も、ユークリッド平行線の傾きは自由にとることができ、双曲平行線との関連はありません。
下のFig.6は、先に双曲平行線を描いた場合です。 黄色い線が基線です。 白線は、観察の便に添えただけのものです。 上半平面では、白線の一端は赤と緑の双曲平行線の交点にあり、他端は黄色い基線に垂直になっています。 この白線の長さが、ユークリッド平行線間の距離になっています。 赤と緑のまだら色のユークリッド平行線は、赤と緑の2本の双曲平行線を重ねて写したものです。
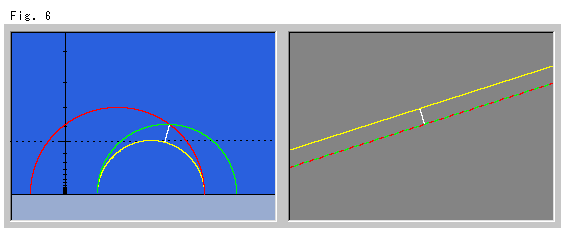
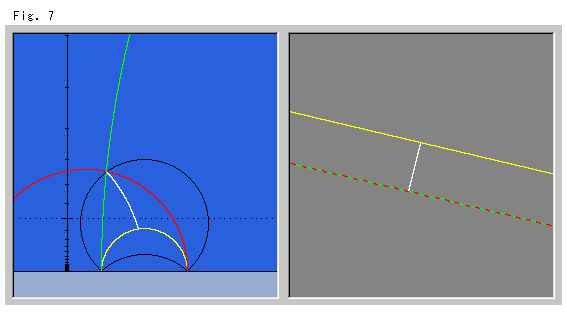
Fig.7は、先にユークリッド平行線を描いた場合です。 赤と緑のまだらのユークリッド平行線が、2本の双曲平行線に別れて写されています。 上半平面上の黒い円弧は、黄色い双曲直線を基線にとった等距離線です。 2本の等距離線の一方をX軸に関して折り返すと、1つの円になります。 もちろん、下側の等距離線を選んで、双曲平行線が通る共有点をとってもかまいません。
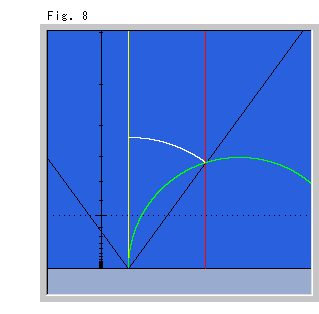
右のFig.8も、先にユークリッド平行線を描いて双曲平行線を得たものですが、上半平面上の黄色い基線を垂直に選んだものです。（ユークリッド平面の図は省いています｡） 等距離線が、円弧ではなく、2本の黒いV字形の直線になっています。 それは、等距離線が無限に伸びたからです。
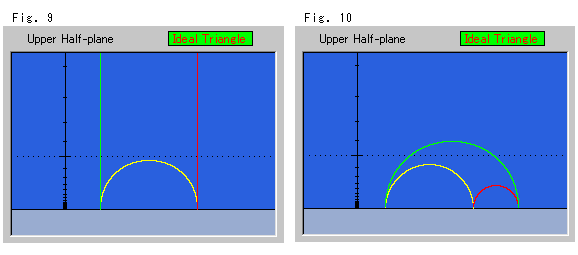
下のFig.9とFig.10は、赤と緑の双曲平行線の交点が無限遠に遠のいて、黄色い基線を含めて理想三角形になってしまっている場合です。 3本の双曲平行線は、平行でありながら同時に三角形です。 双曲平行線(三角形の辺)が見えてはいますが、ユークリッド平行線を描くためのFig.6〜Fig.8のような白線(有限距離)をとらえることができません。 ですから、理想三角形とユークリッド平面との間には、どんなビジュアルな関係も得られません。
このようにして、例外やオプショナルなことがありますけれど、ユークリッドの世界と双曲的非ユークリッドの世界を私たちの目で比べることができました。