双曲幾何ではピタゴラスの定理が成り立たないので、解析幾何の手法がまったく使えません。 これは不便なことですね。
正しくないことは承知のうえで、解析幾何をまねて双曲平面の上に2次曲線を描いてみます。 どのように狂ったものになるでしようか。 それを見てみましよう。
双曲モデル上に描かれる曲線は、まがいものですので、擬○○曲線といったふうに“擬”を付けてよぶことにします。 双曲モデル上でも、以下でユークリッド幾何での焦点、準線、漸近線などに相当するとして扱うものは同じことばでよんでおきます。
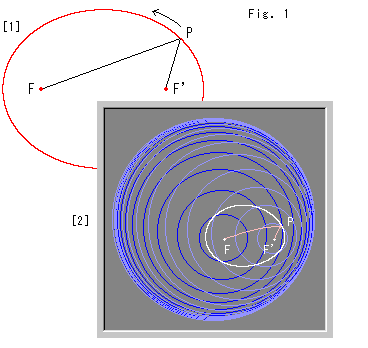
Fig.1をご覧ください。
[1]: ユークリッド平面上に楕円を描く方法の一つです。 点Pから焦点F,F'までの距離の和S
(1)
が一定であるようにして点Pを動かすと、赤い楕円を得ます。
[2]: 白い曲線は、ポアンカレ円板上で式(1)を満たす擬楕円です。 つまり、[1]とまったく同じ要領で描かれています。 2つの焦点間の距離FF'と焦点距離の和Sを[1]と同じ双曲的大きさにとっていますが、描く位置や円板の大きさによって、もちろん違った大きさに見えます。 すこしタマゴ形ですね。 こい青色の同心円は焦点Fを中心とし、うす青色の同心円は焦点F'を中心としています。
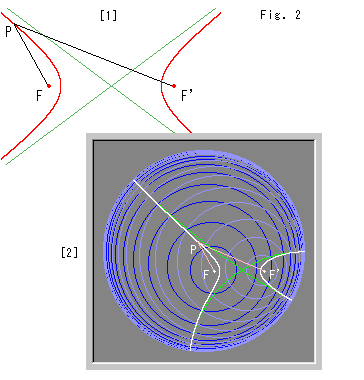
Fig.2をご覧ください。
[1]: ユークリッド平面上の双曲線です。 Fig.1と同様に、点Pと2つの焦点F,F'をとっています。 こんどは双曲線ですから、焦点距離の差Dを
PF - PF' (2)
と、一定に保っていまます。
[2]: 白い曲線は、ポアンカレ円板上で式(2)を満たす擬双曲線です。 緑色の線は漸近線です。 青い円の半径と薄青い円の交点のうち半径の差がDであるものをたどって描かれています。 ずいぶん変わった格好になっていますね。 (ピンク色の双曲的直線PFやPF'がほとんど真直ぐに描かれているのは、円板の中心の近くを通っているからです｡)
Fig.2'は、2つの焦点F,F'間をFig.2より広げてみたものです。 白い曲線は擬双曲線ですが、これではとても双曲線とはよべませんね。 分枝が4つとも1つの焦点F'の方へ曲がって見えます。 それでも、依然として式(2)を満たしています。
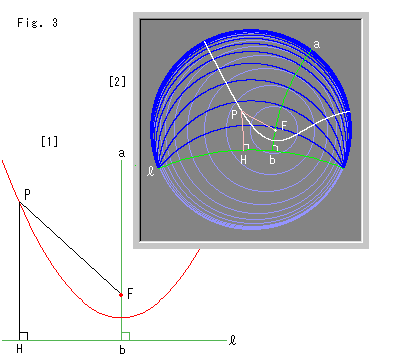
Fig.3をご覧ください。
[1]: ユークリッド平面上の放物線です。 直線abが軸で、直線
が準線です。 放物線の式として、準線からの距離PHと焦点Fからの距離PFが等しい関係
(3)
を用いています。
[2]: 白い曲線は、ポアンカレ円板上で式(3)を満たす擬放物線です。 こい青色の円弧は、準線に関する等距離線です。 うすい青色の円は、焦点Fを中心とする同心円です。
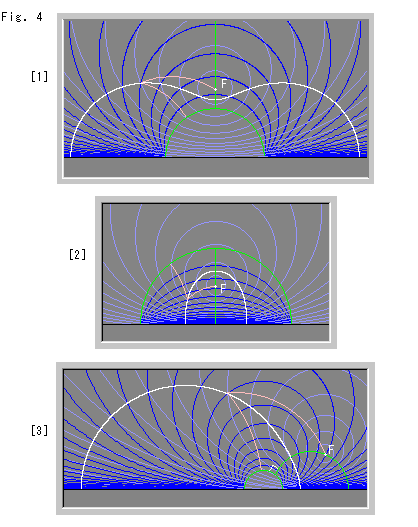
Fig.4をご覧ください。
こんどは、上半平面
をつかいます。 黒い水平な直線がそのX軸です。 白い曲線は、Fig.3の[2]と同じ要領で描いた擬放物線です。 どの擬放物線も、上へは行かずにX軸へ向かっています。 こい青色の円弧とうすい青色の円もFig.3と同様に描かれています。
[1]: 緑色の半円が準線で、その真上に焦点Fをとっています。 緑色の垂線が擬放物線の軸です。
[2]: 準線の半円の中心に擬放物線の軸を垂直に立て、焦点Fを図のようにとっています。
[3]: 焦点Fを右の方にずらせています。 擬放物線は半円を右上からすこし押さえたような形に描かれていますが、その両端はX軸に垂直です。
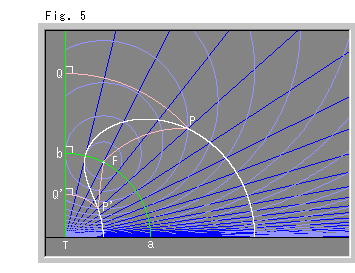
Fig.5をご覧ください。
上半平面上で準線を垂直にして擬放物線を描いてみました。 緑色の直線QTが準線で、緑色の円弧 a-F-b が擬放物線の軸です。 準線の足Tが3つの円弧 PQ, a-F-b, P'Q' の中心になっています。 むろん、PF = PQ, P'F = P'Q' を保っています。 図は点P,P'を PF = P'F にとった場合で、4つのピンクの円弧の長さは QP = PF = FP' = P'Q' となっていています。 描かれた結果は、擬放物線の先がやはりX軸に向かっています。
ランバートの四角形(Lambert's quadrangle)というものと擬2次曲線とのかかわりなどを見ていきます。 右のFig.6は、宇宙を飛んでいるロケットのようですね。 このロケットは、ランバートの四角形を利用して描いたものです。
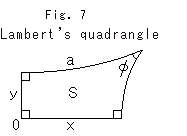
Fig.7がランバートの四角形です。 図はポアンカレ円板上に描いたもので、頂点の一つを原点Oにとっています。 双曲平面上では、角
と辺a,x,yや面積(area) Sとの関係は
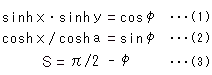
となっています。 長さも面積も双曲的な値です。 双曲線関数(sinhやcosh)については、Ch.29で取り上げます。 ここでは、1より大きくなることもあるsinやcosに似た関数だと思っておいてください。
式(3)を見ると、面積Sは角だけで定まります。 そのを一定に保ちながら、式(1)にしたがってx,yを動かしてみます。
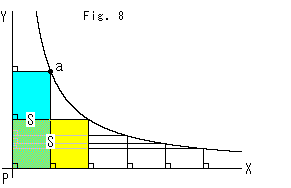
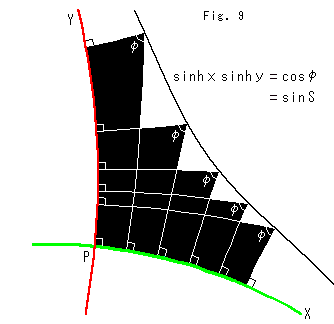
Fig.8は、ユークリッド平面上に描いた双曲線です。 よく知られているように、双曲線上の点aから2本の漸近線におろした垂線でできる四角形の面積Sは、点aが双曲線上のどこにあっても一定です。 ですから、1つの頂点を共有する同一面積の長方形を直行する漸近線に沿って敷いていけば、双曲線ができます。 これと同様なことを双曲平面上でやってみようというわけです。
Fig.9をご覧ください。
黒い曲線はポアンカレ円板上の擬双曲線です。 赤と緑の直線PX,PYは直交している漸近線です。 漸近線PXを双曲的等間隔にきざんで、その上にランバートの四角形を並べています。 角を一定に保っているので、ランバートの四角形の面積Sは、むろん一定になっています。
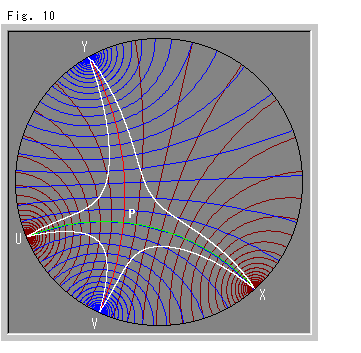
Fig.10は擬双曲線の4つの分枝を全部描き込んだものです。 青い直線(円弧)は、すべて赤い漸近線(円弧)に直交しています。 茶色の直線は、すべて緑色の漸近線に直交しています。 つまり、青と茶色の直線は漸近線を共通垂線とする超平行線の群れの2組です。 超平行線は、漸近線上を等間隔にとって描かれています。
記号U,V,X,Yは次のFig.11で照合します。（漸近線の1つを原点を通るようにしたのが、Fig.6のロケットです。）
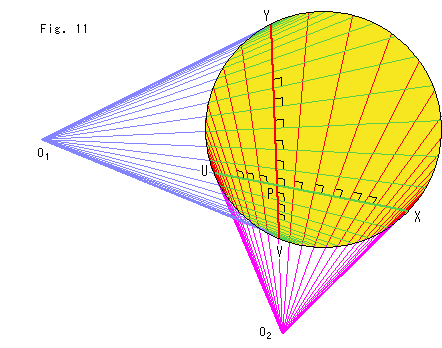
Fig.11は、超平行線がどう仕組まれているかを見るために、Fig.10と同じ超平行線をクラインの円板をつかって描いてみたものです。 直線
Yと直線Vは円板の接線です。 点から出ているすべての射線が弦VYを垂直に切っています。 同様に、点
から出ている射線のすべてが弦UXを垂直に切っています。
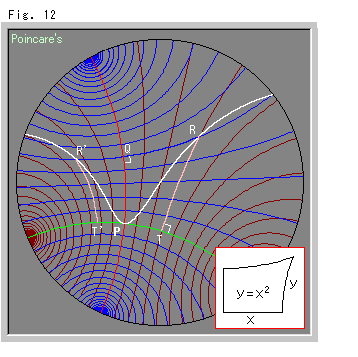
Fig.12をご覧ください。
こんどは、Fig.10と同じ超平行線をユークリッド平面上のXY格子線と見立てて描きます。 白い曲線は擬放物線で、
にしています。
左側でも同様です。 そして、四角形PQRTと四角形PQR'T'ともにランバートの四角形になっています。 しかし、青い超平行線に沿って測った左右の距離QRとQR'は一致していません。
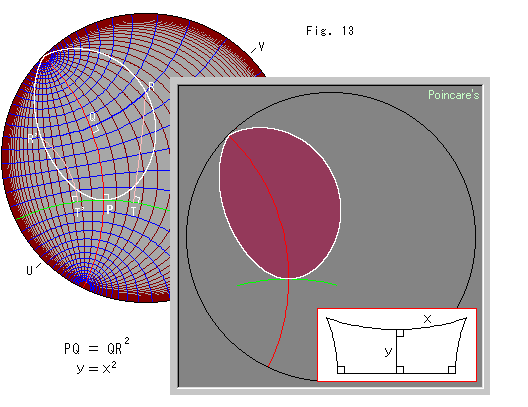
Fig.13をご覧ください。
これもポアンカレ円板上に描いた擬放物線です。 赤い円弧が擬放物線の軸です。 緑色の円弧は、頂点Pで軸に直交しています。 青い円弧はFig.12と同様な超平行線ですが、茶色い円弧は赤い軸に関する等距離線です。 このような超平行線と等距離線を、アンバランスですが強引に、ユークリッド平面上のXY格子線と見立てて描いています。 式はFig.12と似てはいますがちょっと違った
で、QR' = QR を保っています。
ご覧のように、擬放物線が秋の木の葉の縁に似たループになってしまいました。 ちなみに、2つのランバートの四角形が背中合わせなったRR'T'Tは、サッケリ―の四角形とよばれています。
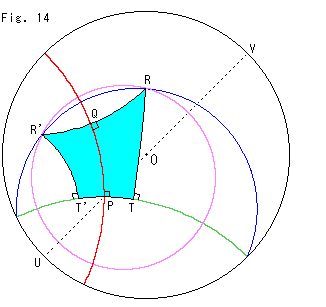
Fig.14をご覧ください。
実は、Fig.13の緑色の円弧と赤色の円弧は、直径UVに関して対称に描いてあります。 ですから、2つのランバートの四角形PQRTとPQR'T'は合同です。 それで、点Rと点R'は頂点Pを中心とする双曲的円周上にあります。 Fig.13の擬放物線上の点R,R'はこんな具合になっているわけです。
緑と赤の円弧がこのように対称でないときは、QR' = QR であっても、ランバートの四角形PQRTとPQR'T'は合同にはなりません。
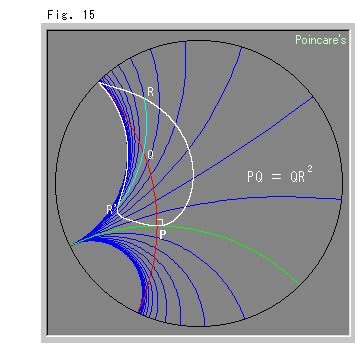
Fig.15をご覧ください。
この白い歪んだ曲線も擬放物線です。 青い円弧は、緑色の直線と平行な双曲的平行線で、擬放物線の赤い軸を等間隔(0.2)に切っています。 青い平行線に沿って左右に等しい距離(QR = QR')をとり、Fig.13と同様に にしたものです。 こんどは、擬放物線の先が尖っています。
擬放物線の軸を赤い円弧にしましたが、平行線の共有点を通るホロサイクルを使うと面白いかもしれません。 ホロサイクルはすべての平行線に直交するからです。
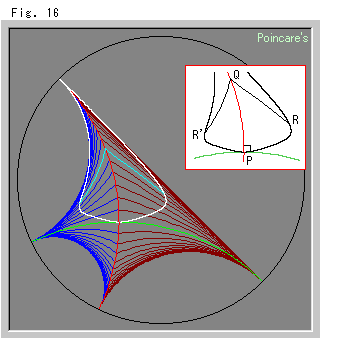
Fig.16をご覧ください。
上のFig.15の右側にも平行線が引けるので、それをとらえて描いたのがこの図です。 図の説明は省きます。
さまざまな擬○○曲線を描くことはいくらでもできますが、これくらいにしておきます。 ここでやったことは、くだらん遊びとも思えますが、双曲平面ではこうも事情が違うことがわかりました。
ところで、双曲幾何に関係したどんな本を見ても、図形としては円と直線のことしか書かれていません。 ほかに名前のつけられた曲線はないようです。 それでは私たちが、
「ある曲線が双曲平面上にあって、それはこういう性質をもっている」
といった話をしてみたいですね。
それには双曲幾何としての計量をもった解析幾何に似たものをつくればよいはずですが、まったく見当がつきません。 いまは課題にしておきます。