ロバチェフスキーらは、2000年以上にわたる平行線の神秘を解いたといわれていますが、なぜ2000年もかかったのでいようか? たしかに思想的な障壁が絶大だったのですが、それとは別にいわゆる機が熟していなかったかったからです。 それは、対数や微積分や双曲線関数などの数学的道具がなかったということです。
双曲線関数をつかった双曲三角法から、距離と角が依存しあうことが出てきます。 それでは、双曲線関数といったものがあると、なぜ、そのような結果を得ることができるのでしようか? 双曲幾何の三角法は、ロバチェフスキーら自身によって証明されています。 私たちが知りたいのは、証明といったものではありません。 ことが旨くいく謎は、双曲線関数そのものの何かにあると思えます。 疑問のもち方は、たとえば、円周率は3.14![]() で、そのことは証明されていますが、なぜ5とか6でないのか、なぜ大きい円でも小さい円でも同じなのか、といったようなことです。 そんな思いで、双曲線関数を見てみます。
で、そのことは証明されていますが、なぜ5とか6でないのか、なぜ大きい円でも小さい円でも同じなのか、といったようなことです。 そんな思いで、双曲線関数を見てみます。
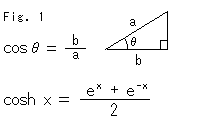
Fig.1は、ふつうのcosと双曲線関数のcosh(ハイパーボリック コサイン)の定義です。 cosとcoshはよく似ているといわれます。 たしかに、公式集を見ると、そうなっています。 でも、まったく異なった定義に見えるものが、どうして似た性質をもっているのでしようか? ふつうのcosは、図のように直角三角形の2辺a,b(長さ)の比とその間の角![]() の関係ですが、双曲線関数coshは何と何の関係でしようか? こんな定義だけを見てもさぱり分かりませんね。
の関係ですが、双曲線関数coshは何と何の関係でしようか? こんな定義だけを見てもさぱり分かりませんね。
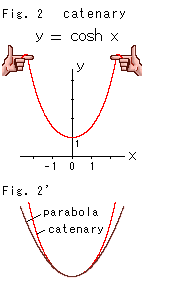
Fig.2は、coshの定義式をグラフにしてみたものです。 この赤い曲線は、カテナリー(catenary, 懸垂線)とよばれているもので、紐を両手にもったときのカーブです。 この曲線の式を求めるのに、昔の人はずいぶん苦労しました。 あのガリレオは、放物線だと思ったそうです。 ガリレオを信じてか、放物線であることを証明しようと格闘した人もいました。
当時はカテナリーの物理的な性質のおよそしか知られていませんでした。 微積分が発明されたのは1670年ころですが、自然対数の底eの記号はまだありませんでした。 1691年、遂にヨハンベルヌーイらによってカテナリーの式が得られました。 双曲線関数が誕生したのです!
Fig.2'で見ると、カテナリーと放物線(parabola)は似てはいますが同じではありません。 coshとcosを級数展開すると、
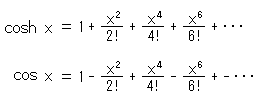
となっています。 放物線は、
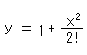
と書けるので、xが小さいところではcoshとほとんど同じです。 しかし、coshとcosは何か一脈通じるように見えますが、似てはいませんね。 双曲線関数が三角関数と似ていることは公式集を見ればなかば肯けますますが、その本質的なところを探っていきましよう。
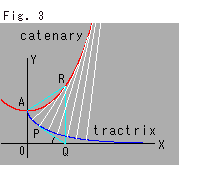
Fig.3をご覧ください。 カテナリーと擬球には、つながりがあります。 赤い曲線がカテナリーで、青い曲線が擬球の母線であるトラクトリクス(tractrix)です。 白い直線は、トラクトリクスに立てた法線です。 (図では、トラクトリクスに沿って等間隔ににとっています。) 法線の包絡線が、カテナリーなっています。 法線はカテナリーの接線です。 カテナリー上の点は、擬球の外側においた接触円の中心の軌跡にもなっています(参照 Ch.22)。 PQはトラクトリクスの接線です。 点A,P,Q,Rは、AR = RP, AO = PQ = 1 の関係になっていて、直線QRはX軸に垂直なっています。
ラクトリクスは
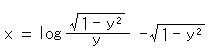
と表わされます。 また、三角関数で
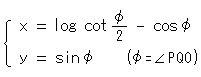
とも表わされます。 さらに、双曲線関数を使えば、tをパラメータとして

と書くこともできます。 ( )内はtanh(ハイパーボリック タンジェント)の定義です。
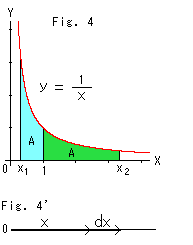
Fig.4をご覧ください。
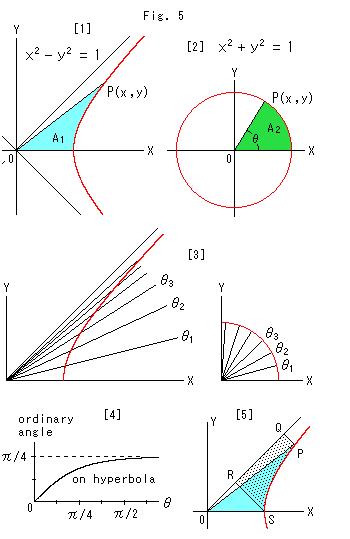
"双曲線"関数というのですから、双曲線について見てみます。 色をつけた2つの部分は同じ面積Aです。 1を境にしたのは、簡単のためです。 このとき、
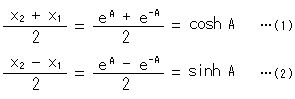
となっているのですが、そのわけを調べてみます。 (式(2)のsinh(ハイパーボリック サイン)は定義です。)
Fig.4'をご覧ください。 双曲線 y = 1/x の下の面積Sは、
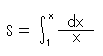
です。 この積分記号の中をよく見ると、長さxとその増分dxの比になっています。 それで、双曲線を長さの変化の割合として説明されています。 また、
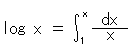
です。 注目されるのは、対数が、指数の逆としてではなく、ある量とその増分の比を積分したものとして定義されるということです。 そして、
ですから、双曲線 y = 1/x の下の面積Sは漸近線の長さxの対数になっていて、その長さxは![]() になっているわけです。 xを
になっているわけです。 xを![]() ,
,![]() として、和の平均をとったのが式(1)で、それと対照的なのが式(2)です。
として、和の平均をとったのが式(1)で、それと対照的なのが式(2)です。
と表わすことができ、空色の部分の面積![]() の2倍がパラメータt、つまり t = 2
の2倍がパラメータt、つまり t = 2![]() になっています。
になっています。
[2]の円では、半径1で、![]() を角として
を角として
と表わされ、半径が1ですから、緑色の部分の面積![]() の2倍が角
の2倍が角![]() 、つまり
、つまり ![]() = 2
= 2![]() になっています。 双曲線と円がこのように類似していることは、1750年ころに発見されたそうです。
になっています。 双曲線と円がこのように類似していることは、1750年ころに発見されたそうです。
t = ![]() にとれば、
にとれば、![]() =
= ![]() です。 しかし、双曲線の角POXが、円の角POX(=
です。 しかし、双曲線の角POXが、円の角POX(=![]() )と等しいのではありません。 そこで、双曲線の角POXをパラメータtで測る(目盛っておく)ことにして、パラメータtを円の中心角
)と等しいのではありません。 そこで、双曲線の角POXをパラメータtで測る(目盛っておく)ことにして、パラメータtを円の中心角![]() で表わします。 そして
で表わします。 そして![]() を、双曲線においては双曲角、それ以外の場合は円角とよんでいます。 円角がふつうの角です。
を、双曲線においては双曲角、それ以外の場合は円角とよんでいます。 円角がふつうの角です。
[3]は、こうしたときの双曲角と円角です。
[4]は、双曲線における双曲角![]() とふつうの角(ordinary angle)との関係です。 円では、円角
とふつうの角(ordinary angle)との関係です。 円では、円角![]() そのままが、ふつうの角です。
そのままが、ふつうの角です。
[5]の点々の部分PQRSは、Fig.4と同様に双曲線から漸近線へ垂線を下ろして囲んだところです。 その面積PQRSは、点Pが双曲線上のどこにあっても、水色の面積POSと一致しています。
上の2つの式を![]() で書いてならべておきます。
で書いてならべておきます。
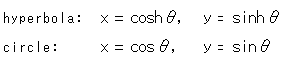
第1の式の![]() は、双曲角で、パラメ―タです。 第2の式の
は、双曲角で、パラメ―タです。 第2の式の![]() は、円角で、実際の角です。 同じ
は、円角で、実際の角です。 同じ![]() でも、双曲線関数にくっついているのは双曲角で、三角関数にくっついているのは円角です。
でも、双曲線関数にくっついているのは双曲角で、三角関数にくっついているのは円角です。
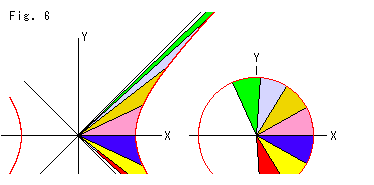
Fig.6は、![]() を0.5の等間隔にとって描いたものです。 同色の扇形が対応しており、どれも同じ面積です。
を0.5の等間隔にとって描いたものです。 同色の扇形が対応しており、どれも同じ面積です。 ![]() を大きくしていくと、双曲線の扇形は細長くなっていきますが、円の扇形は形を変えずに、一周ごとに重なっていきます。 しかし、円と同様に、曲線の内側と外側がどこか分かるような感じがしますね。
を大きくしていくと、双曲線の扇形は細長くなっていきますが、円の扇形は形を変えずに、一周ごとに重なっていきます。 しかし、円と同様に、曲線の内側と外側がどこか分かるような感じがしますね。
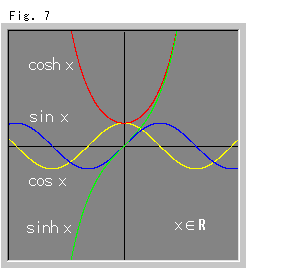
Fig.7は、xが実数の場合の三角関数と双曲線関数です。 三角関数は周期関数ですが、双曲線関数はそうではありません。 そして、たとえば、cosは1以下ですが、coshは1以上です。 ところが、実数xに虚数![]() をつけると、
をつけると、
と書くことができて、両者が完全に結びつきます。 どの式の右辺にも、![]() がありますが、右辺としては実数です。 そして、双曲線関数も周期関数(周期2
がありますが、右辺としては実数です。 そして、双曲線関数も周期関数(周期2![]()
![]() )であるといわれています。
)であるといわれています。
虚数は1400年代から使われていますが、今もちょっと神秘的ですね。 実際、![]() (
(![]() の
の![]() 乗)をすぐにイメージすることなど、たとえ関数論を知っていても容易ではありません。 しかし、虚数
乗)をすぐにイメージすることなど、たとえ関数論を知っていても容易ではありません。 しかし、虚数![]() は、単に、一つの計算ルールを指示しているものだとすることに同意するなら、イメージを追う気遣いは無用となります。
は、単に、一つの計算ルールを指示しているものだとすることに同意するなら、イメージを追う気遣いは無用となります。
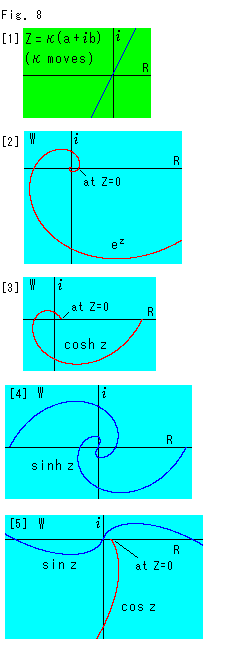
Fig.8は、角が複素数Zの双曲線関数を描いてみたものです。
[1]: z = a + ![]() b として、a = 1, b = 2 にとっています。
b として、a = 1, b = 2 にとっています。
[2]: ![]() は単調増加関数ですが、
は単調増加関数ですが、![]() はぐるぐる回っています。
はぐるぐる回っています。
[3]〜[5]は、双曲線関数の様子です。 たしかに、周期関数になっています。
双曲線関数にFig.4〜Fig.6のような機能をもたせている奴は、自然対数の底eですね。 そのeは、出発点である平行角の公式やロバチェフスキーの公理の話しに出ています(参照 Ch.7,8)。 そうすると、「平行線は真っ直ぐではなくカーブしているのだ」ということを受け入れたのが発端であったわけです。 もとに戻ってしまいました。
自然対数の底eは、ネイピヤーらによって1619年発見されたのですが、そのeを追究しようとすると、数学の大海を漂流してしまうことになるでしよう。 そこで、私たちは矛先を変えます。
虚数![]() を追ってみます。
を追ってみます。
カーブしているものといえば、指数や複素数のグラフは、みな曲がります。 複素数はベクトル(2つの数の組)ですから、変化すれば曲がるのがふつうです。
実数xの sin x や cos x は、虚数![]() を使って、
を使って、
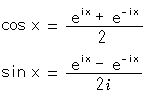
と表わせます。 右辺に![]() が入っていても、虚数に化けたわけではありません。 注目したいのは、三角関数が指数関数で表わされているということです。 いや、なにやら仕掛けの片鱗が見えたような気がしますね。 ちなみに、これら2式から、あの有名な
が入っていても、虚数に化けたわけではありません。 注目したいのは、三角関数が指数関数で表わされているということです。 いや、なにやら仕掛けの片鱗が見えたような気がしますね。 ちなみに、これら2式から、あの有名な ![]() が出てきます。
が出てきます。
指数関数と三角関数と双曲線関数を級数で表わしたものを見比べると、
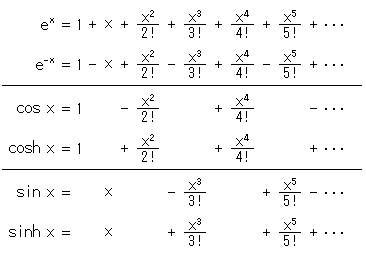
となっています。 三つの関数の類似性を、解析的ですけれどよく、よく物語っていますね。
つぎに、双曲三角法(平面)を見てみます。
三角形ABCの対辺をa,b,cとすると、双曲三角法の正弦定理は
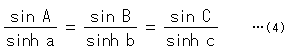
です。 これに式(3)を適用してみます。 すると、分母につく共通因数 -![]() は消えて、
は消えて、
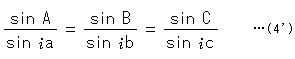
となります。 これは、球面三角法の正弦定理の辺a,b,cに![]() を付けただけの形です。
を付けただけの形です。
双曲三角法の余弦定理は3つありますが、その一つ
に式(3)を適用すると、
となります。 これは、球面三角法の余弦定理の辺a,b,cに![]() を付けただけの形です。他の2つの余弦定理についても同様で、文字がサイクリックに換わるだけです。
を付けただけの形です。他の2つの余弦定理についても同様で、文字がサイクリックに換わるだけです。
双曲三角法の3つの余弦定理を組み合わせると、さらに3つの基本定理が得られます。 そのーつは
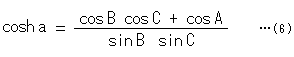
です。 この式こそ、あの驚くべき「三角形の角A,B,Cが与えられると、辺a,b,cが決まってしまう」というものです。
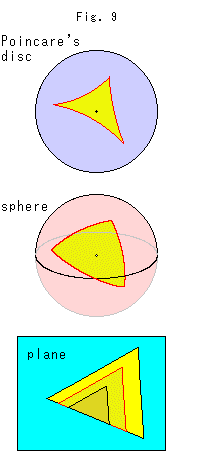
Fig.9は、ポアンカレ円板(Poincare's disc)上と球面(sphere)上と平面(plane)上に三角形を描いたものです。 平面上では、相似三角形をつくれますが、双曲平面上や球面上ではつくれません。
また、この式から、「三角形の内角の和が![]() より小である」ことや、「三角形の面積は
より小である」ことや、「三角形の面積は ![]() - A - B - C である」ことも出てきます。
- A - B - C である」ことも出てきます。
式(6)にも、式(3)を用いると、
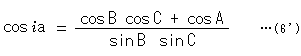
となります。 cosh b, cosh c についても同様です。 左辺の角![]() aから
aから![]() を取り去ると、球面三角法の公式
を取り去ると、球面三角法の公式
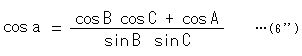
になります。 この球面三角法の場合も、「角A,B,Cで辺a,b,cが決まる」ことに変わりはありません。 そして、双曲幾何とは逆に、「三角形の内角の和が![]() より大である」ことと、「三角形の面積は A + B + C -
より大である」ことと、「三角形の面積は A + B + C - ![]() である」ことが成り立っています。 球面幾何と双曲幾何は、まったく対称的ですね。 なにも驚くべきことはないと思えてくるではありませんか!
である」ことが成り立っています。 球面幾何と双曲幾何は、まったく対称的ですね。 なにも驚くべきことはないと思えてくるではありませんか!
これらのことから、双曲幾何は、虚球面上の幾何だともいえそうです。 虚数半径の球を虚球とよんでいます。 実際、ロバチェフスキーも自分の幾何を「虚の幾何学」とも名付けました。 この“虚”には空想の意味も込められていたそうです。
でも、虚球面上の面積は負になるはずから、これまた合点がいきません。
また、こんなこともあります。
双曲幾何が発見される以前にランバートは、ユーリッドの平行線公理を否定すると、三角形ABCの面積Sは、tを長さの単位で決まる比例定数として
となることを見出しました。 そして、半径rの球面上の三角形ABCの面積Sが
であることと見比べて、彼は、新しい幾何は虚球面上のそれだと推測しました。 たしかに、そんな感じをうけますね。 ところが、惜しいことに、式(7)で t = 1 になるように単位の長さをえらべば、新しい幾何の長さの単位が決まってしまうことを矛盾だと考えてしまいました。 長さの単位なんて、自由に選べるものなのにと。
こんなのは、どうでしようか。
虚球面にもガウス曲率の公式が当てはまると仮定します。 すると、半径![]() の虚球面の曲率Kは、ちょうど K = -1 になります。 つまり、双曲平面を半径
の虚球面の曲率Kは、ちょうど K = -1 になります。 つまり、双曲平面を半径![]() の虚球面だとしてもよい勘定となります。
の虚球面だとしてもよい勘定となります。
あれこれ手探りしてみましたが、双曲幾何のメカニズムの源泉は指数関数、とくに![]() (zは複素数)にあるといえます。 直感的には曲がった空間です。 しかし、十分な視覚化が未だできていません。
(zは複素数)にあるといえます。 直感的には曲がった空間です。 しかし、十分な視覚化が未だできていません。