ユークリッド幾何は無限を避けています。 私たちは、計量や曲率について見てきましたが、そこでも無限が避けられていました。 それでは事がたりません。 ここでは、それに関わる反転について見てみます。 そして、無限について考えます。
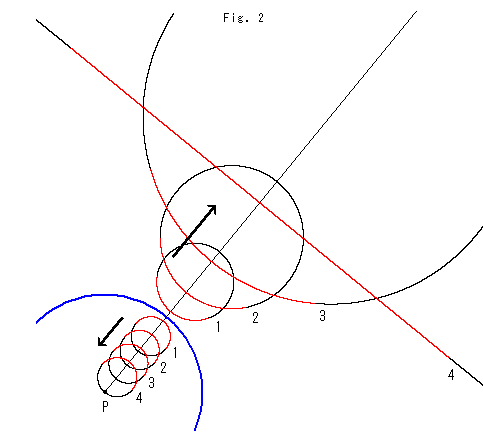
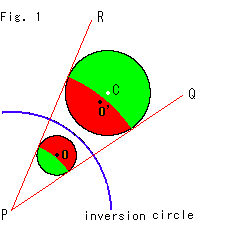
Fig.1は、点Pを中心とする青い反転円(inversion circle)に関して、小さい円Oを反転したものです。 大きい円が反転されてできたものです。 その中心は白い点Cです。 点O'は小さい円の中心Oが反転されたものです。 同じ色のところが対応しています。 色の境界線は反転円と同心の円弧で、直線PQ,PRとの接点を通っています。 小さい円の中心Oは赤い色の側になっているので、それに対応する点O'も赤い色の側にきます。 点O'は大きい円O'の中心ではありません。 つまり、円Oと円O'は、たがいに反転の関係になっていますが、一方の中心が他方の中心と対応してはいないのです。
Fig.2をご覧ください。
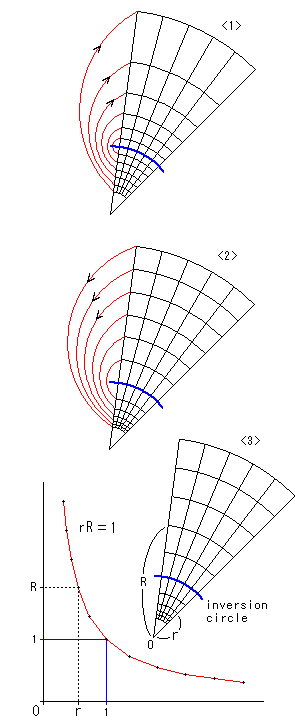
青い円は反転円です。 その内側の円を内円、外側の円を外円と仮によんでおきます。 同じ番号の内円と外円が、たがいに反転の関係になっています。 内円は、すべて同じ大きさで、半周を赤色に染めてあり、外円の同色部分が対応しています。
内円を反転円の中心Pの方へ動かすと、それに対応する外円は、大きくなりながら遠のいていきます。
内円4の円周は中心Pに達しています。 このとき、それを反転した外円4は半径無限大の円になっています。 そして、その一部分だけが図のように見ることができます。 それは、ふつうの円ではなくて直線です。
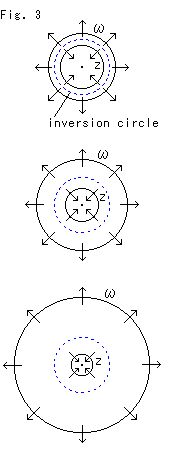
Fig.3をご覧ください。 青い点線の円は、半径1の反転円で、中心を原点にとっています。 円Zは反転円の内側にあり、円
は円Zを反転したものです。 円Zの円周上の点を複素数Z、円の円周上の点を複素数とします。 複素数を用いるここでの理由は、平面上の点を座標を含めて一つの文字で表わせる便利があるためです。 円Zを小さくしていくと、円は急激に大きくなっていきます。 円Zと円の関係は
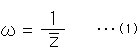
です。 分母をZでなく
(共役複素数)としているのは、円Z上の点Pと反転された円上の点P'が、反転円の中心(原点)から見て同じ方向になるようにとっているからです。 この反転の式(1)は、一次変換とよばれている変換式
で、a = d = 0, b = c = 1 にとったものです。 一次変換は各点での角を変えない、いわゆる等角写像です。 ですから、反転も等角写像になっています。
式(1)のZを0に限りなく近づけると、
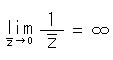
となります。 ここでの無限大
には正負を考えていません。 このとき、 = となるのですが、それを
=
と決めつけます。 つまり、
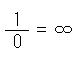
とします。 ふつうは、分母がゼロの分数は定義できないのですが、あえてこうします。 (気になるなら、極限で考えてください｡)
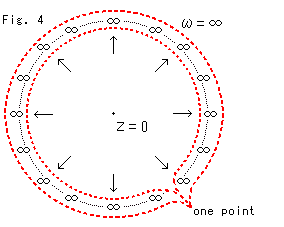
Fig.4は、Zが Z = 0 で1点になり、は無限の彼方の四方八方へ飛び散ってしまっているイラストです。 無限大になったは、無限の速さで飛び去りつづけています。 このままでは、Zとがつねに 1対1 であることにはなりません。 無限遠もふつうのところと区別せずに、同じように扱えると便利ですが、それには、どこでも 1対1 でないと困ります。 そこで、数学者たちは、飛び散ったの点を全部ひっくるめて1点とします。 無限の彼方を1点にしぼめるというのではありません。 このは、東西南北どこにでも現れて、それでいて1点です。 数学者って、こんな勝手なことをするんですよ。 しかし、原点からの距離が有限である点を反転したものは、やはり点です。 そして、Z = 0 のときのZも点ですから、そのときのは無限大でありかつ点だとする方が、リクツに合うようにも思えます。 なにしろ、無限遠では常識が通用しなくて、非常識が巾を利かすところですから。 ともかく確かに、1点だとすれば、Z = 0 も含めて、Zとはつねに 1 : 1 になります。これは逆に Z = のときは、 = 0 となって、1対1 が保たれるということです。 そこで、1点だとしたところの点に名前をつけて、無限遠点とよび、記号で表わされています。
この名前は、実のところ適切ではありません。 なぜなら、無限に遠いところの点と読めるからです。 無限に遠いところの点であってもよいのですが、この点は辻つま合わせをするだけのものです。 ほかで対象とする以外の点なら、フィクションであってもかまいません。
もう一つの不適切なことは、無限遠点の記号として、無限大と同じ“”が使われていることです。 無限遠点は点であり、無限大は大きさです。 は、無限に遠いところを指している場合もあります。 さらに、の正負を区別する(負なら-と書く)ときと、正負の概念を外している場合があります。 無限遠点は、正でもあり負でもあり、また、そのいずれでもないというシロモノです。 ですから、私たちは無限遠点を、ではなく、なるべく
で表わすことにします。 そして、その意味を固めていくことにします。
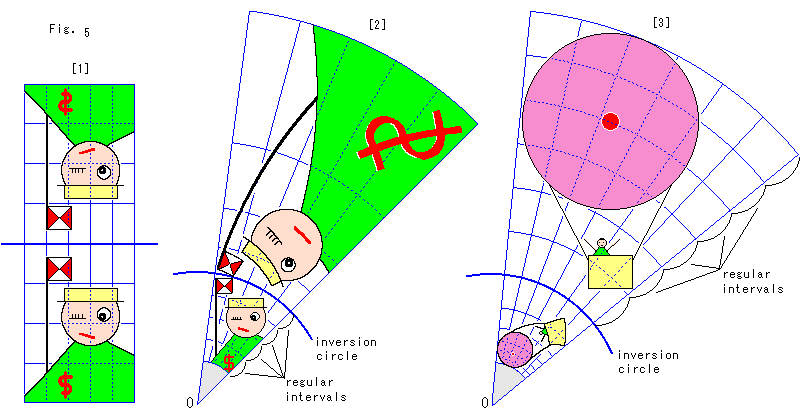
上のFig.5は、面白半分に描いたものです。
[1]: ふつうの線対称です。
[2]: 青い反転円(inversion circle)の内側に[1]と同じ絵を描いて外側へ反転させたものです。 格子は[1]と対応させていません。 格子の同心円は、先に反転円の内側に絵を描いたので、右図<1>のように青い反転円の内側で反転円の中心Oからの距離を等間隔(regular intervals)にとり、それを反転円の外側へ反転させて描いています。 内側と外側はたがいに反転になっているので、同心円の引き方に特別な意味はありません。
反転は等角写像です。 反転されて大きくなっている方をみると、旗竿が曲がっていますし、服がスカートのように裾の方で広がっています。 しかし、旗竿と洋服のへりがなす角は、まったく変わっていません。 つまり、形や大きさが変わっても、各点での角は保たれているのです。
たしかにそうです。 けれども、ちょっと不思議です。 [1]は対称の軸に関して、たんに折り返しものですね。 この[2]は折り返した[1]の一方を絞り他方を引き伸ばした、つまり歪めたものと考えられます。 そうすると、歪めているのに、どうして角が変わらないのでしょうか？ 角が保存されるという事実を認めることは容易ですが、この不思議を解きたいものですね。
また、各点での物差しや分度器を格子にあわせて歪め、それで測った絵は少しも歪んだことにはなりません。 これは当然で、不思議とは感じません。 一方が不思議で他方がそうでないのは、どうしてでしようか。 しかし、いまは先をいそぎましよう。
[3]: こんどは、青い反転円の外側にふつうに絵を描いて内側へ反転させました。 それで格子の同心円は、右図<2>のように反転円の外側で中心Oからの距離を等間隔にとり、それを反転円の内側へ反転させています。 円は、反転円の中心を通らないかぎり、反転しても円ですが、その中心はずれます。
右図<3>は、特定の範囲の同心円を等間隔に引くようなことはしないで、反転の様になるように描いたものです。 赤い双曲線 rR = 1 上を等間隔にとったrとRを半径とする同心円からなっています。 簡単のために反転円の半径を1にとっていますが、反転円の大きさを変えても、同じ格子パターンになります。
Fig.6は、反転によって(直線も含めて)曲線がどう変わるかを描いたものです。
青い円が反転円で、同色のものがたがいに反転になっています。 ただし、反転円の中心Oを通る黄色の直線は、その上の点は移動しますけれども、直線としては変わりません。 太く描いてあるところは、部分どうしで対応しているところです。 黒い曲線は、正方形とそれを反転したものです。 むろん、反転円の円周上の点は不動です。
点Pが反転円の中心Oへ向かって進んでいます。 このとき、その反転された点P'は左下の遠くへ行っているはずです。 同様に、点Qも反転円の中心Oへ向かって進んでいます。 その反転された点Q'は右下の遠くへ行っているはずです。
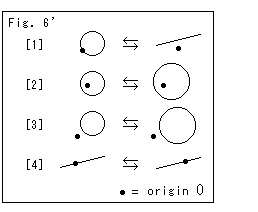
Fig.6'の囲みに反転の定理をイラストしました。
黒いスポットは反転円の中心です。 反転円によって円や直線は、
[1]: 反転円の中心を、通る円と通らない直線が相互に移りあう。
[2]と[3]: 反転円の中心を、通らない円と通らない円が相互に移りあう。
[4]: 反転円の中心を通る直線は、変わらない(不動直線)。
となっています。
これは、私たちの目で見ることのできる範囲ではＯＫです。 しかし、Fig.6の点Pや点Qが原点に近づいて行くとき、それらの対応点である点P'や点Q'は、どうなのでしようか。 点Pが原点Oに到着するまでは、点Pと点P'は、ずっと1:1です。 いま点Pは、原点Oに到着して、静止しているとします。 そとき点P'は、無限の彼方で、無限のスピードで遠のいている(動いている)にちがいありません。 それでも、１：１は破れません。 同じ状況が、点Q'にも生じます。 点Pと点Qは同じ1点である原点Oにいますが、点P'と点Q'は異なる方向にいます。 それにもかかわらず、Fig.4では、点P'も点Q'もひっくるめて同じ1個の無限遠点だとしています。 本当に、それでよいのでしようか？
反転がどういうメカニズムで行われのかはわかりました。 しかし、反転を実感するには足りません。 そこで、モデル円板と上半平面
が反転によって移りあうことに目をつけて、その様子を見てみることにします。 それは、円と半平面の対応ということに注目すれば、モデル円板と上半平面に限ってのことではありません。 円はどんな円でもかまいません。 以下では、上半平面を指しての話しでないところでは、たんに半平面とよんでおくことにします。
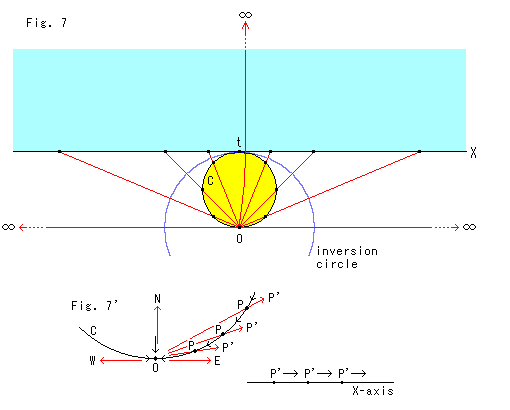
Fig.7をご覧ください。
青い大きい円が、点O中心とする反転円です。 その中に黄色の円Cがおかれています。 円Cは、反転円の中心Oを通り、反転円に内接しています。
円Cは反転によって、その円周は水色の半平面のX軸になります。 赤い線は、その対応を示しています。 そして、円Cの内部は無限に広がった半平面全体になります。 反転円の上端tで内接しているところの点は、反転されても動きません。
Fig.7'をご覧ください。
円Cの円周上の点Pが点Oであるとき、その点Pは反転によって何処へ移るのでしようか。 Fig.4のように爆発していながら、それでいて1点であるとすることで本当によいのでしようか？
少し離れたところから点Oに近づくという極限で考えてみます。 右の方から円Cに沿って点Oへと点Pを動かします。 すると、反転された点P'は、斜めの赤い矢印のようにX軸上へ移って、X軸上を右へ右へと移動して行きます。 円C上の点Pが点Oに達したときは、反転された点P'はX軸上の右の方の無限の彼方Eへ飛ばされているはずです。
左の方から円Cに沿って点Oへと点Pを動かして点Oに達したときは、これとは逆で、点P'はX軸上の左の方の無限の彼方Wへ飛ばされているはずです。
円Cの内部の上の方から垂直に点Oに達したときは、反転された点P'は上の方の無限の彼方Nへと飛んでいるはずです。 X軸が上の方の無限に遠いところでループになっていると思えば、やはり点P'はX軸上にあることになります。
いずれにしても、点Oにおける反転は、そこに達するときの方向にによって、その逆の方向に反転されるのだと捉えることができるということです。 しかし実際には円C上の点は内部を含めてかってに動くことはありません。 それでは、最初から点Oのところにじっとしていた点は、どうなるのでしようか。 やはり、有限のところにはいないで、住所不定の曲者の無限遠点に化けていると考えるほかありませんね。
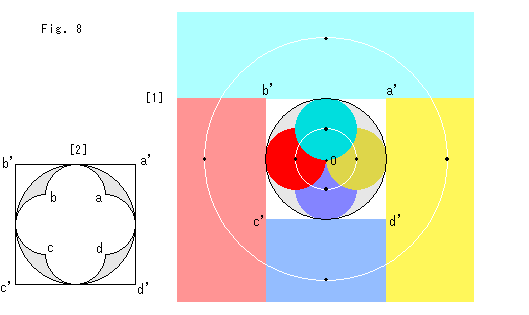
Fig.8をご覧ください。
面として反転円の内側と外側がどのような関係になっているかを見るために色分けしてみます。
[1]: 反転円の内部を濃い色にして、同種の色の領域が対応していることを表わしています。 反転円の内側の4つの円は、反転円に内接し、反転円の中心Oを通っています。 反転円を囲んでいる正方形a'b'c'd'の四隅の白いところは、それぞれのすぐ内側の灰色の領域に対応しています。 黒いスポットは、反転円の内側の4つの円の中心とそれらの対応点です。 小さい白い円は、4つの円の中心を通る円です。 その反転されたものが大きい白い円です。
[2]: 正方形a'b'c'd'と対応する4つの円の部分です。 なにかこう思わせぶりな感じがしますが、ちゃんと反転のルールにかなっています。
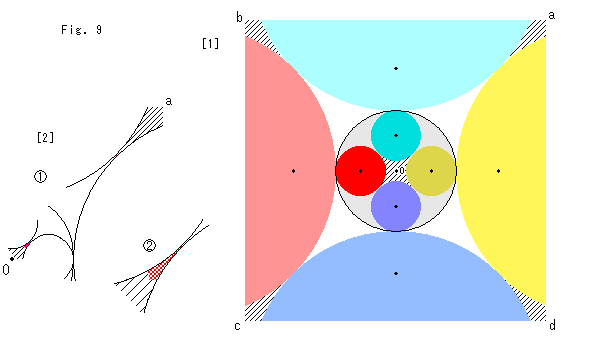
Fig.9をご覧ください。
反転円に内接する4つの円を重ねずに並べてみました。
[1]: 4つの円はいずれも反転円の中心Oを通りませんから、それらを反転したものはやはり円になっています。 しかし、4つの円の中心(黒いスポット)が反転されたところは、ユークリッド的な中心ではなくて、反転円の方へ片寄っています。 色による対応はFig.8と同様です。
[2]: [1]の大きな四隅a,b,c,dの斜線の領域は反転円内の斜線部分に対応したところですが、その四隅に実際に描かれてあるのは反転円内の極一部に対応したところです。 
の赤く見える範囲がそれです。 
は、そこを拡大したものです。
Fig.10をご覧ください。
反転円の中にその中心Oを通る内接円Cをセットして、こんどは、その内接円Cの中にFig.4と同様に4つの円を並べました。 反転円の内部の灰色のところは、反転円の中心Oを通る直線
と反転円に接する直線
の間のモザイクのところに移ります。 青い円以外の円C上のものは、直線と
の間に移ります。 縞模様のところは、垂線パターンは垂線パターンに、斜線パターンは斜線パターンに対応しています。 直線に接している反転円内の青い円は直線から上の半平面に移ります。
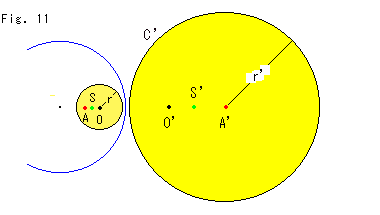
Fig.11をご覧ください。
反転した円の中心ともとの円の中心がどう移り合っているかを見ておきます。 反転円によって、円Cの黒い中心Oは円C'の黒い中心Oに移ります。 円C'の赤い中心A'は円Cの赤い点Aが対応しています。 点Sと点S'は、反転しても相似的な同じ位置を変えない点です。 相似的に同じというのは、OS / r = A'S' / r' であることを指しています。
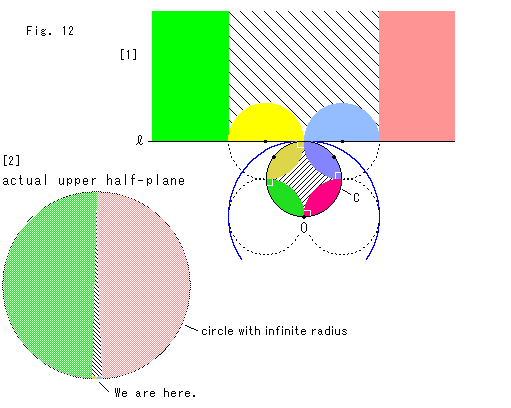
Fig.12をご覧ください。
反転円の中心Oを通る内接円Cをセットして、その円周に直交する4つの円を描きます。
[1]: 円Cと4つの円に囲まれた4つの
形の領域の反転の様子です。
この円Cをポアンカレ円板とすると、その内部の円弧は双曲的直線です。 そして、直線
から上の半平面は上半平面であり、直線が上半平面のX軸ということになります。 円C上を見ると、緑と赤の点Oのところが共有点になっています。 そうすると、上半平面にある緑と赤の領域は無限の上の方で共有点をもっているにちがいありません。 そして、その共有点は1個だと考えるほかありません。 さらに、円Cの円周は閉じたループですから、直線は直線ではなくて、半径無限大の円の一部だと考えられます。
[2]: それを想ったイラストです。 無限大は描き得るものではないのですが、あえて想像しました。 それは、実際の半平面(actual Upper half plane)は半径無限大の円(circle with infinite radius)でできているとしたものです。 図の下端に私たちはいます(We are here.)。
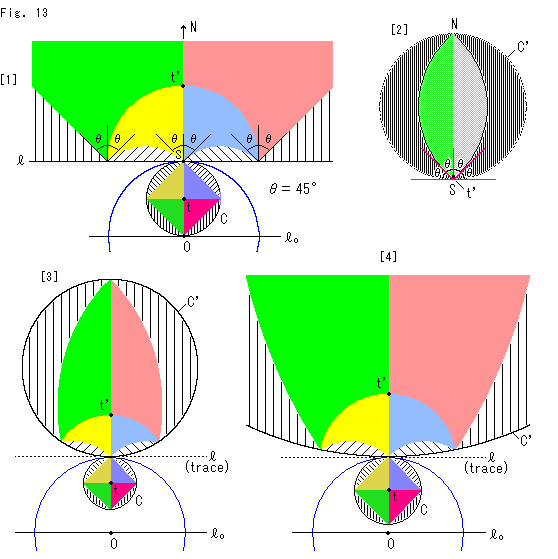
Fig.13をご覧ください。
形を図のように
形に変えてみました。
[1]: 反転での各領域の対応は、ご覧のとおりです。 点tは円Cの中心で、点t'はその対応点です。 点Sは、直線と反転円と円Cの共有点です。 直線は反転の中心Oを通り、直線と平行です。 角
は、どれも45
になっています。 そして、特徴的なのは、Fig.12と比べて、反転されて無限に広がった赤と緑の領域の端が直線と45になっているということです。
[2]: 上にならって実際の上半平面をイラストしたものです。 円C'は直線を半径無限大の円周の一部と考えたもので、もとは円Cです。 私たちがいる下端Sと同様に上端Nを描きました。 しかし、これで正しいでしょうか？
[3]: それを知るために、円Cを小さくして反転の中心Oから離してみました。 反転は等角写像ですので、45のところは45、90のところは90のままで変化はありません。 点線はもとの直線の跡(trace)です。 そして、点線から上に円C'が形成されています。
[4]: 円Cをちょっと大きくしたところです。 見た目にも[1]に近づいています。 円Cを連続的に大きくしていって、反転の中心Oを通るようにすると、[2]になります。 したがって、[2]は正しいといえるはずです。
しかし、円C'を半径無限大の円だとするには、円C'上の計量を定めなければなりません。 それは上半平面の計量
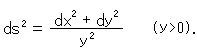
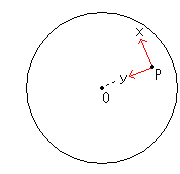
と本質的に変わりないにちがいありません。 円C'上の点Pがどこにあっても、右図のようにX,Y方向をとって、この計量を適用すればよいと思えます。 けれども、具体的にそれを算出することは、いまの私たちには手に負えません。
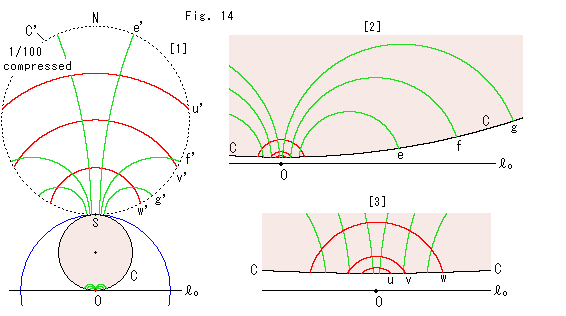
Fig.14をご覧ください。
作図的には、反転円の半径を2にしておいて、ポアンカレ円板としての円Cの半径を0.996くらいにとると、反転円に接する円Cが反転の中心Oを通っているように見えます。 それは誤魔化しですけれど、その円Cを反転すると、閉じたループである円C'が得られます。
[1]: 円C'を1/00に圧縮して(compressed)描いたものです。 反転されたものの大部分は円C'上の点Sのごく近くに片寄るので、円C上の点Oの近くに双曲直線を引いて反転させました。
[2]: 点Oの近くを拡大したものです。 ちょっと見ると、[1]の円C'上の反転されている曲線は円C上の曲線を相似拡大されているように見えますが、そうではありません。 曲線に付けられた記号で見比べてください。 円Cと直線の間のギャップは、作図の誤魔化しが露見したものです。 そのままに眺めてください。
[3]: 赤い曲線の様子を見るために、点Oの近くをさらに拡大したものです。
描いてはみたものの、これで半径無限大の円内を推測するには裏づけがとぼしいですね。
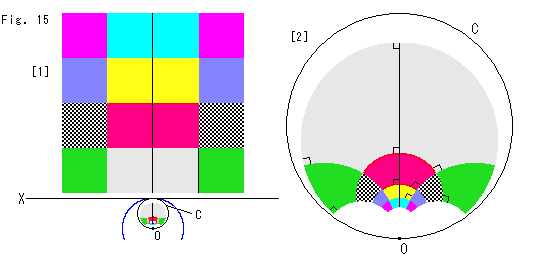
Fig.15をご覧ください。
上半平面に直交格子を描いて、反転してみます。
[1]: 直交格子はX軸からすこし浮かせて描かれています。 そのため、反転された格子は反転の中心Oを通る円Cの内部に入っています。
[2]: 円Cを拡大して見やすくしたものです。 反転は等角写像ですので、どの領域の隅も直交しています。
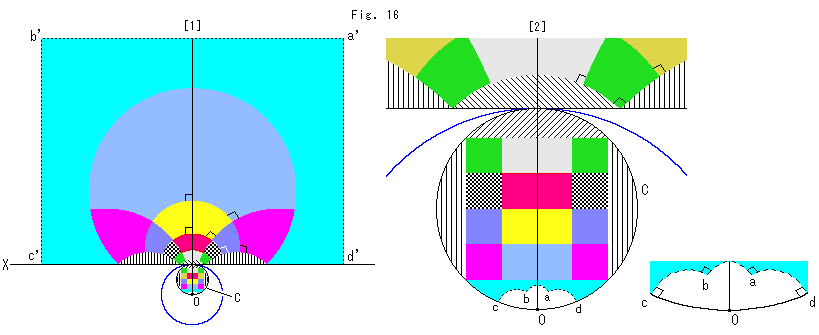
上のFig.16をご覧ください。
こんどは、円Cにぴったりはまる直交格子を描いてみました。
[1]: それを反転させたものは、たがいに直交する円弧からなっています。
[2]: 円CとそれがX軸と接している付近を拡大したものです。 縞模様や水色のところは格子の外側です。 円Cの内部に空き領域があるのは、反転円の中心Oに近い白いところだけです。 点線で区切った水色の領域は、[1]の直線Xから上の水色の長方形の外側に対応しています。 水色と白色の境界は4つの円弧からなっていて、a,b,c,dがa',b',c',d'に移っています。 右下に描いてあるように、白いところのどの隅も直角です。
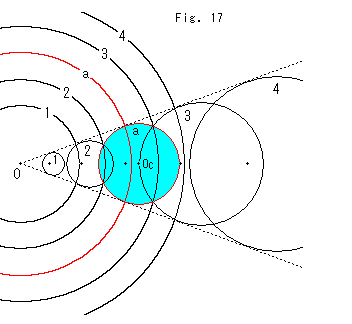
Fig.17をご覧ください。
反転円の大きさが違うとどうなるでしようか。 水色の円を異なる大きさの反転円で反転します。 反転円は中心をOにとった等間隔の同心円です。 赤い反転円aの大きさは、それで水色の円Cを反転させると、ちょうど元の円に重なるように選んだものです。 この赤い反転円aは円Cの中心Ocを通っていません。 そして、円としてはもとの円とぴったり一致しますが、反転された中心はずれています。 円Cを反転円1で反転させると円1になり、反転円2で反転させると円2になります。 また、円Cを反転円3で反転させると円3になり、反転円4で反転させると円4になります。 各円内の黒いスポットは円Cの中心Ocが反転されたところで、すべて反転円の中心Oの方へ偏っています。
反転円が元の円C切っているときは、その反転円と元の円と反転された円の三者が交わっています。 反転された円の大きさは、反転円の内側へ反転されたものも外側へ反転されたものも、点線のように反転円の大きさに比例しています。 この点線は円aと反転円の中心Oだけで定まり、反転円の大きさには依存しません。
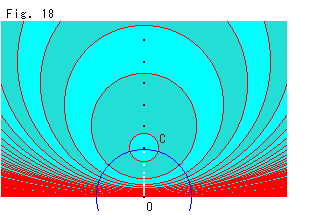
Fig.18をご覧ください。
円が反転円の1つの半径を切りながら大きくなっていくと、その反転された円はどうなるでしようか。 反転円の半径を切る円ならどんな円でもよいのですが、反転しても円として動かない円だと見やすいので、それで描きます。 そのような円を不動円とよんでおきます。
青い反転円の外側の近くに中心をとって、不動円の1つ円Cを描きます。 不動円の中心は、反転円の内側にとることはできません。 また、不動円の半径は選んだ中心によって定まります。 反転円の中心Oと円Cの中心を通る直線上で、反転円の外側に円Cの中心から等間隔に点をとります。 図は、そのようにとった点を中心とする不動円を描いていったものです。 黒い点は、反転したそれぞれの円の中心ですが、対応するもとの点は白い点です。 円としては不動でも、その中心は動いています。 Fig.11をもう一度見てください。 まったく動かない点は、反転円の円周上だけです。 黒い点を上の方へとっていくと、白い点は反転円の中心Oへ収斂していきます。
これを見ると、不動円は無限に大きくなっても、反転円の中心Oを内部にもつことはできません。 不動円の中心は、上の方の無限の彼方へ行っているはずです。 そして、反転円の外側ではなく、不動円の中心Oを通る直線を境界とする半平面全体になっています。 その半平面は、反転しても反転円の内部と外部の点が入れ替わるだけで、やはり半平面です。 これは、不動円とは関係なしに、半平面を反転したものは、個々の点を別にすれば、同じ半平面になるということです。 円の内側の色を交互に濃淡にして見やすくしていますが、濃淡いずれの円が半平面になっているかをいうことは、もちろんできません。
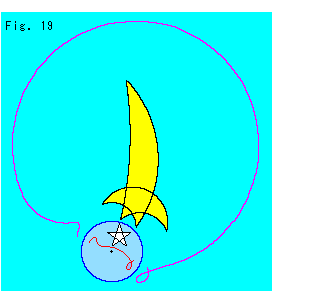
Fig.19をご覧ください。
勝手な線を青い反転円の中に描いて反転してみたものです。 これで、ちゃんと反転のルールにかなっています。 星が巨大なバナナになってしまいました。 もとの星に直すには、同じ反転円でもう一度反転するほかありません。 鏡映や線対称では、2回すると平行移動したのと同じことになります。 しかし反転では、1点か円周以外の図形を別の場所にもとの姿で移すことは、どうしてもできません。
これで、反転とはどいうことをいっているのかが、実感として大分はっきりしてきました。 いずれも理屈からすれば当たり前のことばかしでした。 しかし、Fig.6'までを見ただけでは掴めませんでしたね。 でも、反転円の中心は爆発するとか、「すべては1点なり」などと神秘がかった話しのところだけは、まだスッキリしません。
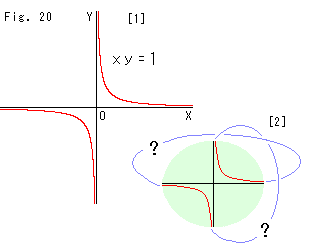
反転円の内部と外部の関係は、Fig.5のところでも見たように、双曲線で表されます。 それで、双曲線そのものを見てから反転をもう一度考えてみます。 双曲線の端はどうなっているのでしようか。
Fig.20をご覧ください。
[1]: この赤い双曲線を追って空想すると、上を向いた曲線は無限に昇っていき、神秘界を通って、再び下の方から現れる。 そして、左へターンし、進んでいく、、、。 そして、またも現れる。 こんどは右からだ。
[2]は、夢見た人の航跡です。 神秘なゾーンは無限遠点の巣だったのではないでしようか。
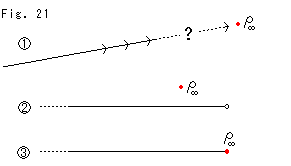
Fig.21をご覧ください。
まずもって、直線は本当に無限にまで伸びているのでしょうか？
は、それに疑問があるイラストです。 ユークリッドは、「線の端は点である」、｢線分はいくらでも伸ばせる」といっています。 彼は、“無限に”とはいわずに“いくらでも”といっています。 数学的には、直線は限りなく伸びていて端がないといわれています。（数学基礎論では無定義語です） のように無限遠点といものが在るとしても、数直線上とは限らないで超然としています。 数の仲間とはいい難いものです。 無いかもしれないし、無数にあるかも知れません。 そして、必要に応じてセットできるものです。 たとえば、
のように数直線の先端に無限遠点があるとして万事好都合なら、それでよいのです。 まことに得体の知れないものですが、とても有用です。 数直線のかわりに平面をとっても、まったく同様に考えます。BR>
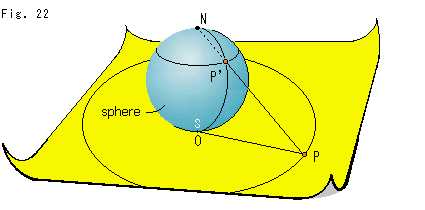
Fig.22は、一つのトリックです。
紙面(平面)の上に原点Oとって、そこへ球面(sphere)の南極Sを置きます。 そうして、紙面上の点Pと球面の北極Nをむすんだ直線が球面と交わるところを点P'として、点Pと点P'を対応させます。 点Pが原点Oから遠のけば、紙面をそれだけ広げていきます。 この紙面はいくらでも広げられるとします。 すると、点Pが無限の彼方へ行ったとき、点P'は北極Nへ行きます。 点Pがどの方向へ行っても、点P'の行き着く先は北極Nです。 そこで、平面上で無限遠点をさがす代わりに、この球面を平面(点Pを点P')だとして、北極Nを平面上の無限遠点に対応する点とすれば、巧くいきます。 平面上の点Pと球面上の点P'は例外なく1対1になっています。 ただし、平面上には無限遠点の居場所は定められていません。
数直線にならって、この平面を数平面とよぶと、球面は数球面とよべることになります。 もちろん、球面上の距離は、平面上の距離として測らねばなりません。 点Nは無限遠点とみなされているのですから、一端を点Nとする距離はすべて無限大です。 この北極を無限遠点とした球には、リーマン球という名前がついています。 リーマン球は、平面は無限に大きな閉じた曲面だと捉えることを許すものです。
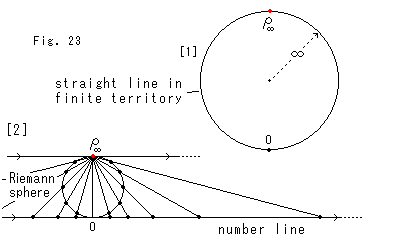
Fig.23をご覧ください。
[1]: Fig.22のの赤い点と、私たちがいる有限域で直線(straight line in finite territory)だとする半径無限大の円をくっつけたものです。 この“直線”は、まさに、いくらでも伸びています。 無限遠点すら通り抜けて、ぐるぐる回ることがでるものです。 現に、Fig.21の北極Nも通り抜けられるように見えています。
[2]: よく見かける数直線(number line)と無限遠点との対応関係を表現したものです。 円はリーマン球(Riemann sphere)です。 この全体を強いて描いたのが、[1]というわけです。
さて、このような考えを反転に取り入れてみましよう。
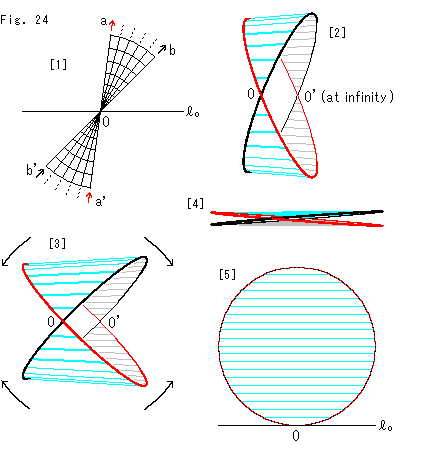
Fig.24をご覧ください。
[1]: 無限の彼方へ行くと、そこで止まるのではなくて、ぐるっと回って元のところへ戻るというのですから、Fig.5の扇形は図のように描いておくべきですね。 赤い矢印aのように遠ざかれば、無限遠を経て矢印a'のように帰ってきます。 黒い矢印についても同様です。
[2]: 無限遠も含めての想像画です。 横縞の線は面を表現するだけのもので、反転の目盛りとは関係ありません。 帯の巾が途中から狭くなって、無限遠(at infinity)である点O'で赤と黒の縁が位置を交換しています。 これはメビウスの帯のように捩れているのではありません。 もう一つの反転円があって、その中心が点O'であるようにも感じられますね。
[3]: ポアンカレ円板を反転にあわせた[1]の扇形は、中心角180の半円です。 そうするために矢印のように広げます。
[4]: 中心角を180近くまで広げたところです。
[5]: 中心角を正確に180したものを真上から見たところです。 赤と黒の縁が完全に重なって一つになっています。 交点O'は消滅しています。 これは半径無限大の円板です。 しかし、Fig.13の円板と同じではありません。 ここで得た円板は、作成過程からわかるように、左右の縁を区別することができないのです。
Fig.25をご覧ください。
上のFig.24の[3]の面は円筒状です。 そのまま矢印のように広げて円板が得られました。 広げたのはOO'を軸として回転させたのですから、その回転に沿って面を形成してみます。
すると、はじめはのよう球扇形になり、となって、最後には球面になりります。
Ch.22の最後の方で半球と上半平面の関係を見ました。 そのときのことを思い浮かべながら、すすめます。
まず、円板モデルの円板は開円板ですし、上半平面ではX軸は含まれていません。 実際、円板モデルの周や上半平面のX軸上では双曲三角法は破綻してしまいます。 双曲幾何のモデルには、いくらでも遠い所はありますが、無限遠は無いのです。 ですから、無限遠点を通り抜けて、ぐるぐる回るという考え方は無用です。
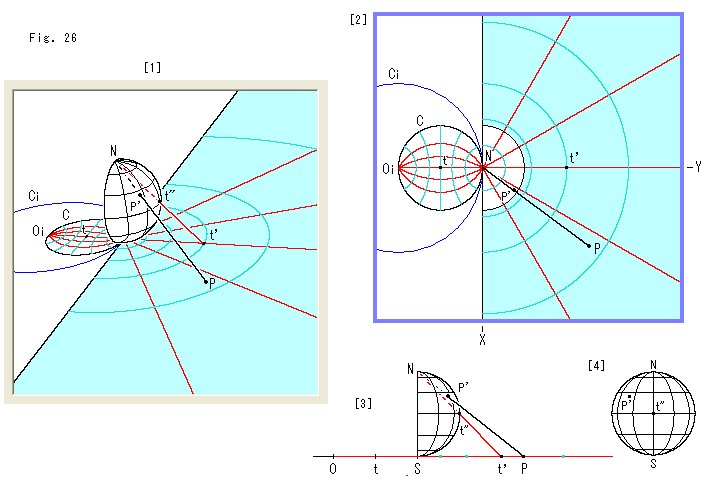
Fig.26をご覧ください。
半球を上半平面のX軸上に置いて、北極Nからの射線を利用します。
[1]: 水色のところが上半平面です。 北極Nからの射線で半球面上の点P'は上半平面上の点Pに移ります。 赤い放射状の直線と緑色の同心円は、地球儀のように半球に引いた径緯線を同様に移したものです。 円板Cはポアンカレ円板です。 そこにある赤と緑の曲線は、上半平面上の曲線を反転で移したものです。 Ciが反転円で、点Oiはその中心です。 ポアンカレ円板Cの円周が反転円の中心Oiを通っています。 ポアンカレ円板Cの中心tと上半平面上の点t'が対応していて、射線Nt'が半球面上の点t"を通っています。
[2]: 真上から見たところです。 半球面の経緯線は省いています。
[3]: 上半平面を水平にして見たところです。
[4]: 半球面を正面から見たところです。
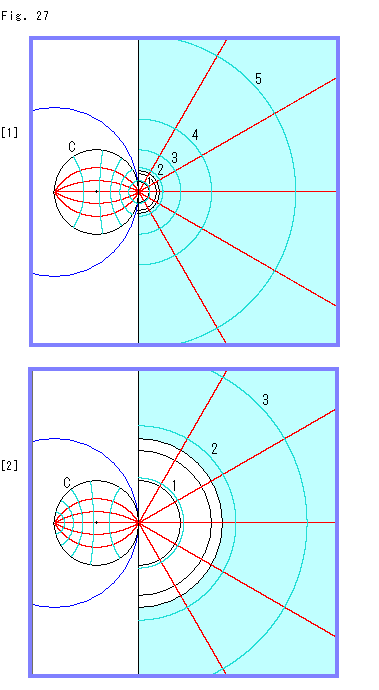
Fig.27をご覧ください。
上では、半球の半径をポアンカレ円板Cの半径と同じ大きさにしました。 そのため上半平面上に移されたものを反転してできたポアンカレ円板C上の曲線のパターンがバランスのよいものになりました。
半球面の大きさを、経緯線を地球儀と同様にとったままで変えてみます。
[1]: 半球面の半径をポアンカレ円板Cの半分にした場合を上から見たところです。 赤い曲線のパターンに変化はありませんが、半球面の緯線に対応する緑色の曲線がずれています。 ポアンカレ円板C上では、右の方へ偏っています。 上半平面上では、同心円がその中心へ寄ってきています。 同心円に付けた番号は中心に近いものからの順です。
[2]: 半球面の半径をポアンカレ円板Cの2倍にした場合を上から見たものです。 曲線の偏りは、[1]と逆になっています。
上半平面上の緑色の曲線をFig.26のままで固定しておいて、半球面の大きさを変えると、右上の図のようになります。 半球面を小さくすると緯線は上へ偏り、大きくすると下へ偏ります。
また、上半平面の目盛りに合わせて射線を引くと、下図のようになります。 基準点 (Y = 0) はどこにとってもよいので、射線が赤道を通るのを基準にとっています。 南極Sのところの無限大に負号をつけてあるのは、基準点より左側であることを示しているだけで、上半平面には含まれていません。 比較のために、下にユークリッドスケール(Euclidean scale)を添えています。
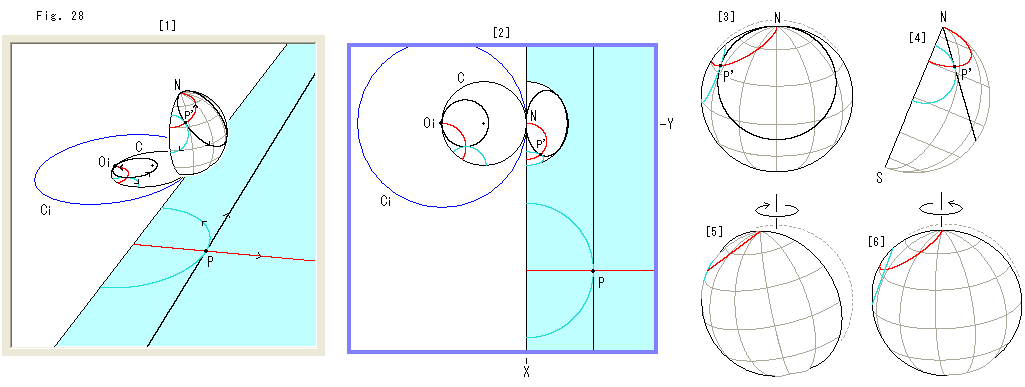
上のFig.28をご覧ください。
上半平面のXY軸から離れた点Pを通る3曲線を引いてみます。
[1]: X軸とY軸に平行な2直線と半円です。 矢印で曲線の流れの対応を表現しています。
[2]: 真上から見たところです。
[3]: 半球面を取り出して、こちら側へ向け、よく見えるように北極Nを手前へ少し傾けています。 点線は半球面であることがわかりやすいように傾ける前の跡を残したものです。
[4]: それを真横から見たところです。 黒い曲線が直線状になっています。（Ch.22の下の方をもう一度みてください。 Ch.14, Ch.17も参照。）
[5]: 矢印のように半球面を回すと、赤い曲線が直線状になって見えます。
[6]: 同様に半球面を回すと、緑色の曲線が直線状になって見えます。
半球面を適当に回すと、赤黒緑のどの曲線も直線に見えるので、どの曲線も半球面を平面で切ってできる切り口の円であることがわかります。 そして、黒と赤の曲線は、それらをつくる平面が北極Nを通っているので、上半平面では直線になります。 その平面上を北極Nから出る射線が這うわけです。 緑色の曲線をつくる平面は、北極Nから出る射線に貫通されるだけです。
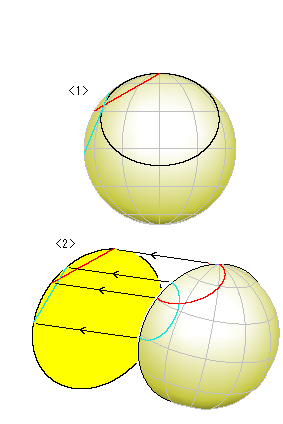
これらのことから、半球面の縁を円周とする円板はクラインの円板であることがわかります。 右図の<1>のように半球面を真っ直ぐに立てて正面から見ると、赤と緑の曲線がともに直線状に見え、黒い曲線は楕円に見えます。 <2>は、半球面上の赤と緑の曲線だけをその円板へ正射影した様子です。
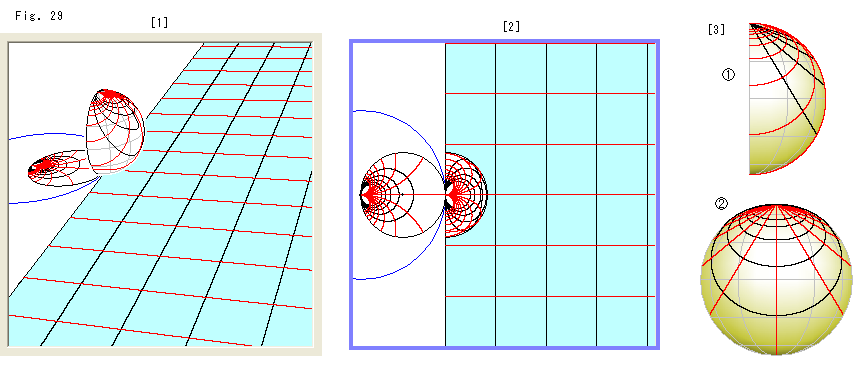
上のFig.29をご覧ください。
もう描くまでもないことですが、上半平面上に格子線を描いて射影される様子を見てみます。
[1]: 半球面上で赤と黒の曲線が直交しているのが見えます。 上半平面上の格子線を反転したポアンカレ円板上の曲線も直交しています。
[2]: 真上から見たところです。 半球面を透かさないで描いています。
[3]: 半球面を2方向から見たものです。 では黒い曲線が真っ直ぐに見え、では赤い曲線が真っ直ぐに見えています。
上半平面にはX軸は含まれていません。 双曲モデルとしてではなく、ふつうの上半平面でなら、X軸を含めたものを考えることができます。 そうすれば、半球面の考えで無限の彼方も反転域に入れることができます。 そして、Fig.4のことにも矛盾は生じません。
でも、Fig.24の[1]のことが気になりますね。 それに、Fig.10で見たようにX軸と円板Cの外側との間の反転は、直線と直線の間のモザイクのとろに移ります。 そこを見ておきましよう。
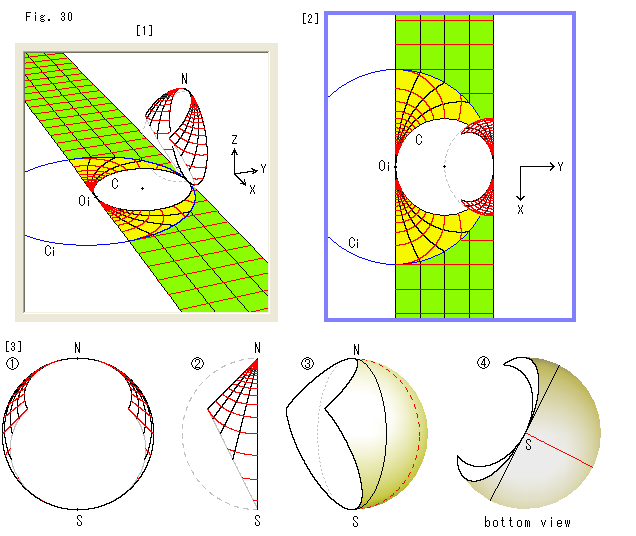
Fig.30をご覧ください。
[1]: 黄色いところを反転すると、緑色の無限に伸びた帯状の領域全体に広がります。 それを北極Nからの射線でリーマン球上に移すと、左側の半球面の部分を図のように覆います。 半球面の無用なところは切り落としています。
[2]: 真上から見たところです。 半球面を透かさないで描いています。
[3]: は、欠けた半球を正面から見たところです。 は側面です。 切り口が円であることがわかります。 は、上半平面との関係で用いる半球面を補って、少し回して見たところです。 反転円内の半分がこの欠けた球面に移るわけです。 
は、の真下からの眺め(bottom view)です。
こうしてみると、反転円Ciの内部全体の反転を見るには、欠けた球面が2個要ることになりますね。
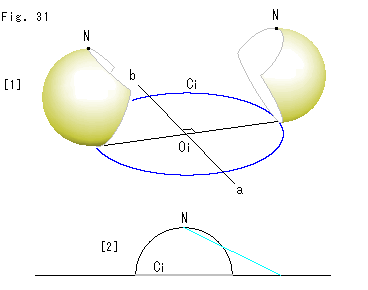
Fig.31をご覧ください。
[1]: 反転円Ciの向かい合ったところに欠けた球面を置いてみたものです。 こうすると北極Nが2つできます。 それでは、反転円の中心Oiを通って2つの欠けた球面の下端をむすぶ直径に直交する直線ab上の点は、どちらの北極Nと対応するものとすればよいのでしようか。 両方をとったのでは、1対1の対応が破れます。
[2]: やはり、1個の半球面で考えるべきですね。 図のように反転円Ciに丁度かぶさる半球面で工夫してみましよう。
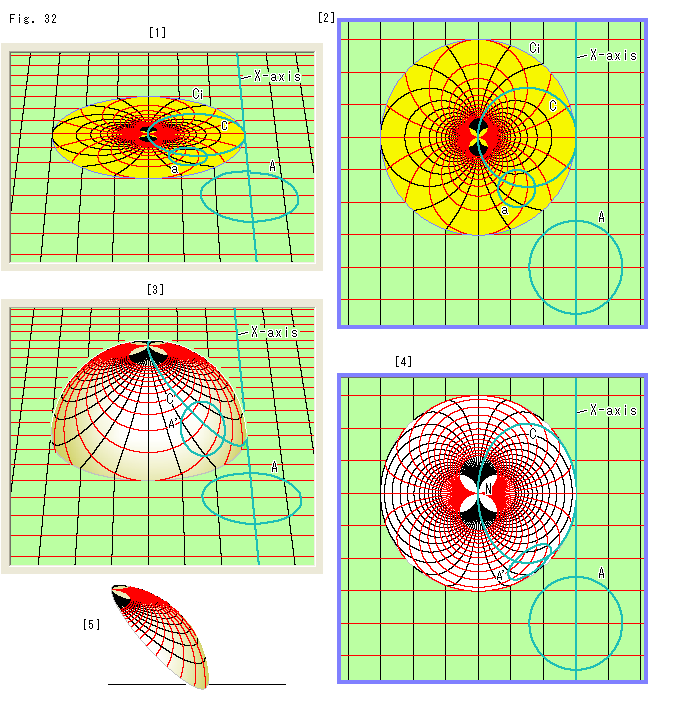
Fig.32をご覧ください。
[1]: 反転円Ciの外側に直行格子を描いて、それを反転して反転円Ci内へ移したものでっす。 濃い緑色の直線は上半平面を設けるときのX軸(X-axis)です。 円Aは、そのX軸上に中心をとって描いたもので、円aと対応しています。 円CはX軸にたいおうするもので、ポアンカレ円板の周に相当します。
[2]: [1]を真上から見たところです。
[3]: 反転円Ciに半球面をかぶせます。 そして、平面上の格子線と円Aを北極Nからの射線で半球面へ移しました。
[4]: [3]を真上から見たところです。 [2]と見比べると、粗密はちがいますが、曲線のパターンがよく似ていますね。
[5]: 半球面から円Cで切り出した球冠です。 上半平面と対応するのは、この球冠のところだけです。 もちろん、45傾けたままで使用しなければなりません。
幾何模様ではいま一つわからないので、上の方で描いたマンガを登場させてみましよう。
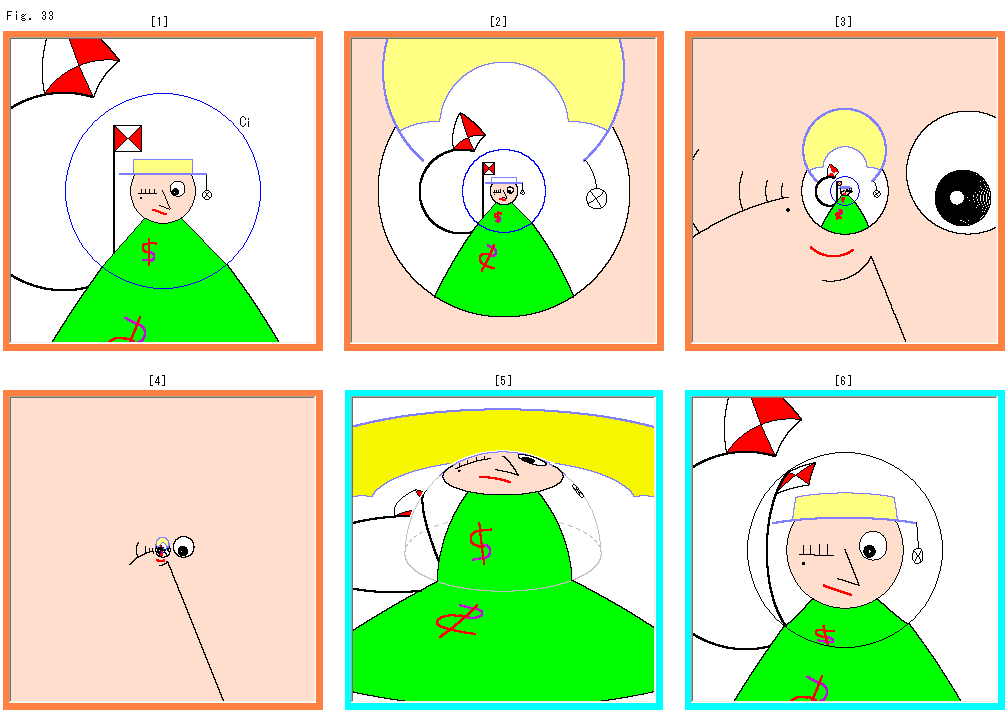
上のFig.33をご覧ください。
[1]: 反転円Ciの内部のすべてを反転しました。 鼻の上端の付け根が、反転円の中心になっています。 反転されたところは、画面に限りがあるので、ほんの一部しか見えません。
[2]: 縮小して、見える範囲をすこし広げたところです。 帽子が逆さまになって、顔の肌色が現れました。
[3]: 見える範囲をさらに広げたところです。 左の方からウィンクしたまつ毛とほくろが現れ、右の方からは目玉が現れました。 下の方からは、赤い口と鼻が出てきました。 反転されたもののそれぞれを見ると、左右にあったものは左右を逆にし、上下にあったものは上下を逆にしています。 しかし全体で見ると、右にあったものは右に、左にあったものは左にというように位置を交換してはいません。 上下についても同様です。
[4]: もっと見える範囲を広げたところです。 反転円Ciやその付近が見えなくなってきました。 ただ、反転円Ciの中心から伸びている鼻の稜線だけが画面の端までいっています。
こんな風では、反転を一望にすることはできません。
[5]: 反転円Ciにかぶせた半球面上に、反転されたものを北極からの射線で移したところです。
[6]: [5]を真上から見たところです。 おや、[1]とさほど変わりないではありませんか。 半球の中に入って眺めても、裏返って見えるだけです。 失望！
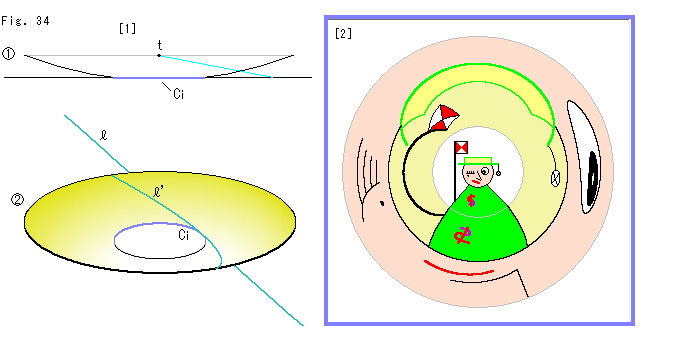
Fig.34をご覧ください。
こんどは、底を抜いたお皿のような形の球帯でやってみます。 Ch.1でのことを思い出してください。
[1]: 球帯は球面を輪切りしたもので、その断面はのようになっています。 球帯の切り取られた底部は反転円Ciと一致させてしています。 上底の中心tからの射線で、反転されている図形を球面に移します。 は、球帯を斜めから見たところです。 直線は反転円Ciに接しているもので、上半平面のX軸に構成できるものです。 曲線
は点tから出る射線で直線を球帯上に移してみたものです。 射影の中心tが球面の中心ではないので、この曲線は大円ではありません。
[2]: 反転されているマンガをこの球帯に射線で移して、それを真上から見ています。 球帯の中央の穴の中に反転円Ci上の原像が見えています。 その外側は球帯上の像です。 これでやっと、反転されたものの様子を一望にすることができました。
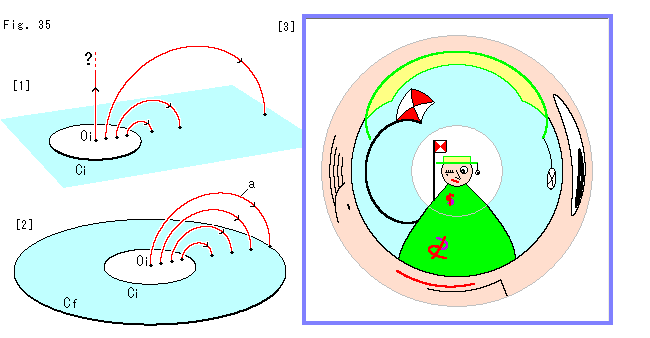
Fig.35をご覧ください。
反転は折り返しの一種です。 それなら、反転の式や1対1のことは忘れて、半径方向に折り返してみましょう。
[1]: ふつうの反転の場合の点の移動を赤い曲線で表現しています。 反転円Ciの中心Oi上の点の反転先は何処といえないので、一応、上向きの矢線にしています。 ?印はその意味です。
[2]: 円板Cfの中央に反転円Ciを置きます。 そして、反転円Ci上の点を赤い曲線のように半径方向に折り返します。 水色の部分の巾と反転円Ciの半径は同じでなくてもかまいません。 図の場合は按分比例で半径方向に拡大しています。 反転円Ciの中心Oi上の点の反転先は、折り返し方向によって決まります。 しかし、その方向の定めようがありません。 図の曲線aは、あえて折り返し方向をえらんだときのものです。 そうしなければ、[1]の?印の曲線と同様な状態です。
[3]: 反転円Ciに描いたマンガを円板Cfへ折り返して、真上から見たものです。 当然ですが、上のFig.34のとあまり違いません。
反転の話では、原像とその反転された像が対比されています。 それではパッと移り変わった結果だけを見ているので、変化の様子といったものがいま一つわかりません。 本のページをめくるように反転の過程というものが見えるとよいですね。 反転の式は
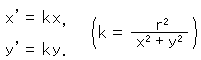
と書けるので、kの代わりに 
を使って、tを変化します。 k'は、いわば反転の効きめです。
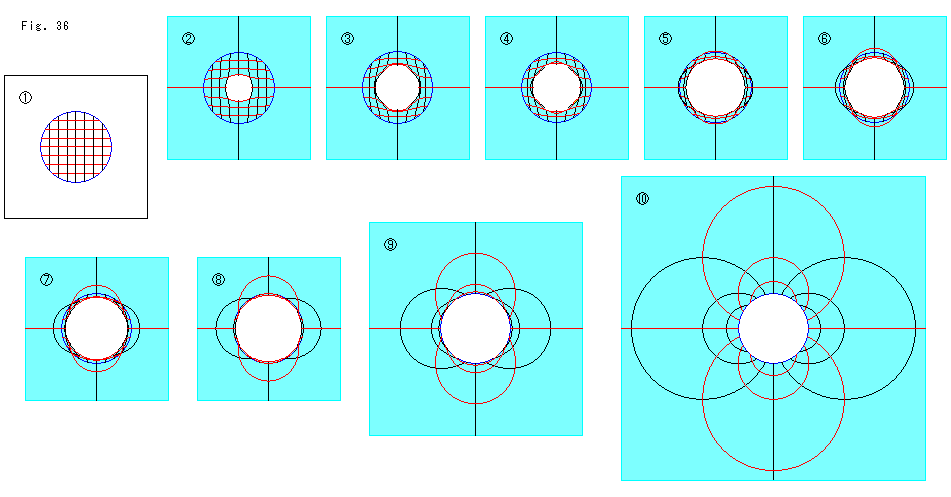
上のFig.36をご覧ください。
反転の効きめをつかいます。 は反転円上の格子線です。 反転を開始するや、反転円の中心は四方に飛び散ります。 は反転の効きめを働かせて間もなくの状態です。 水色のところは反転された曲線が占めている範囲です。 反転の効きめを次第に高めていくと、〜
のようになります。 
では反転円の中心を通っていなかった曲線も反転円の外側へはみ出しはじめています。 そして、外側へ移った曲線がだんだん大きくなっていきます。 最後のは、ふつうに反転したときのもので、すべての曲線が反転円の外側へ移っています。