一つの平面を上半平面
からユークリッド平面へ連続的変化させることをこころみます。 といっても、どのように計算すればよいのか、私たちにはわかりません。 上半平面の計量をユークリッド計量へと連続的に変化させるとか、曲率を-1から0へとゆるやかに変化させればよいはずですが。具体的な演算方法がつかめないのです。 そのため、イラストで考えていきます。
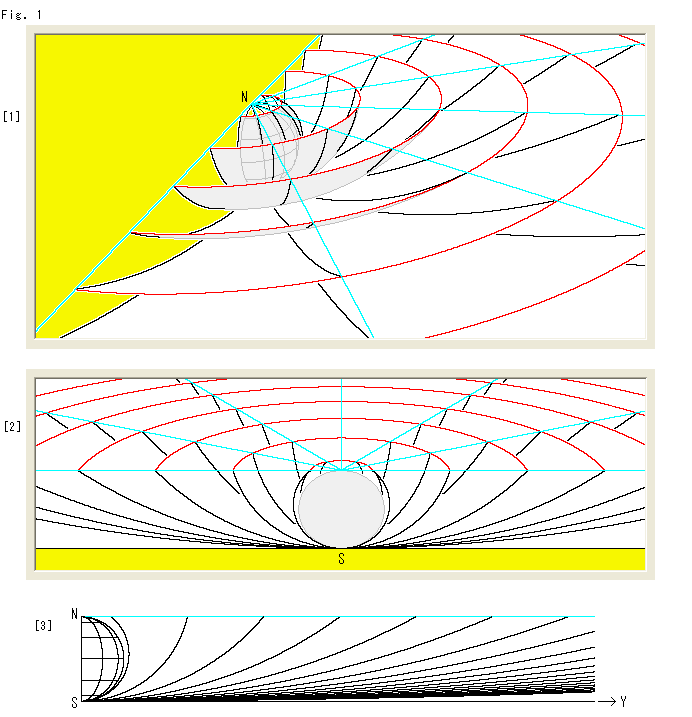
Fig.1をご覧ください。
半球面を射線で上半平面に移すのを曲面の連続的な変形でイラストしてみます。
[1]: 北極点Nを取り去ります。 点を取り去った跡も点ですが、それを広げていきます。 北極Nであったところの各面の赤い縁は、つねに北極Nと同じ高さです。 図は球面の中心を上の方へずらしながら、その下部を切って描いています。
[2]: 半球面の後方から見たところです。
[3]: 真横から見た切断面です。
これでわかるように、半球面の表皮をどんどん押し広げて、どこまでも際限なく広げていったものが上半平面です。 そのときは、半球面の表皮は平坦になって、南極Sと同じレベルになっているにちがいありません。
私たちが見たり考えたりしている上半平面は、無限に広がっている曲面のごく一部だといえます。 つまり、上半平面は平坦化してしまった曲面です。
こんな風に、連続的に双曲幾何とユークリッド幾何をつなぐことができれば、面白いですね。 でも、それは不可能なことがわかっています。 では、どのように不可能なのでしようか。 玉子の殻はどのようにしても平坦にならないという話だけでは、いま一つ足りません。 ベルトラミーの擬球をいじくってみましよう。 以前にCh.21で、上半平面から擬球を作り出しました。 そのことを思い出してください。
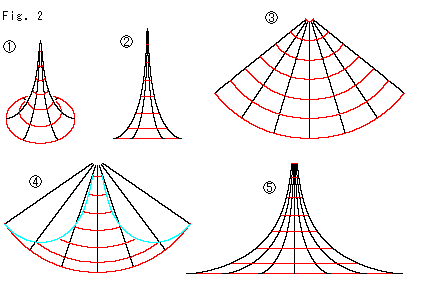
Fig.2をご覧ください。
擬球
を
のように真っ直ぐに立てます。 黒い母線の長さを保って平坦な扇形に広げると、
のようになります。 赤い線は曲がっていますし、長さは擬球のと同じではありません。 
は赤い線の長さを擬球のそれに一致させたものです。 赤い線の両端が水色の曲線上にきて、黒い半径と遊離しています。 こんどは、赤い線を真っ直ぐにして、長さを擬球のと合わせると、
のようになります。 すると、黒い線は曲がり、ながさも不揃いになります。
ということで、不可能なことがイラスト的に証明されました。
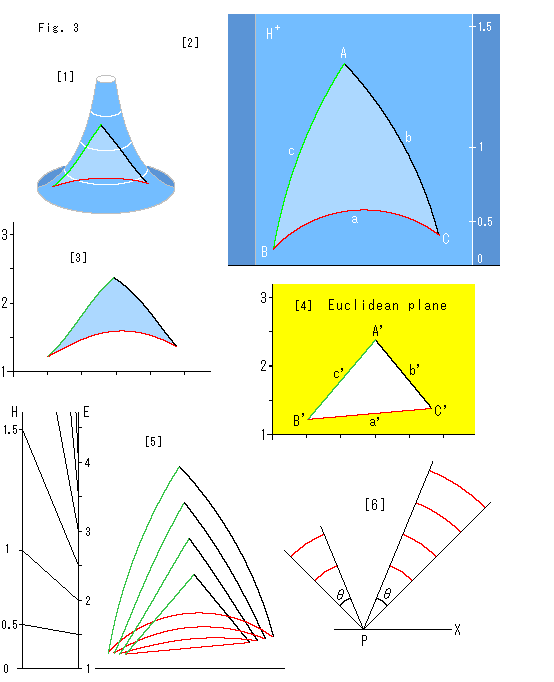
Fig.3をご覧ください。
もう一つ考えられるのは、擬球をいったん上半平面に変えて、その上半平面をX軸方向とY軸方向に伸縮すれば、ユークリッド平面にできるのではないかということです。 やってみましよう。
[1]: 擬球上に三角形をえがきます。
[2]: それを上半平面に移したところです。 右側の目盛りは双曲値です。 X軸から1のところを基準(Y = 0) にしています。 この双曲三角形の要素は
辺 a = 1.6, b = 1.11, c = 1.24
角 A = 104.85
, B = 33.95, C = 38.72
内角の和 A+B+C = 177.52
です。
[3]: これをユークリッド三角形に変えようとします。 上半平面での値を hX, hY、ユークリッド平面上での値を eX, eY と表して、
eX = hX / hY
eY = 1 + log hY
を使って、スケールを均等にしました。 それだけでは、当然、三角形の辺は真っ直ぐになりません。
[4]: ユークリッド平面(Euclidean plane)上では、2点間の距離は直線に沿って測るのですから、3頂点を直線でむすびます。 これで、ユークリッド三角形が得られました。 この三角形の要素は
辺 a' = 1.8, b' = 1.27, c' = 1.53
角 A' = 79.16, B' = 44.08, C' = 56.75
内角の和 A'+B'+C' = 180°
です。 角だけでなく、辺も大きくなっています。 それは、たぶん、yが1より大きいところで上半平面の計量を使っているからでしよう。
[5]: 上半平面[2]からユークリッド平面[4]へ、[3]をステップにして一気に移ることはしないで、平面の伸縮と辺の直線化を同時に追ったものです。 左側のHは双曲目盛りで、Eはユークリッド目盛りです。 横方向の目盛りの変化をイラストするのは煩雑ですので、省きました。 Ch.19を参照してください。
[6]: 横目盛りのかわりに、添えたものです。 上半平面上の双曲的線分は、X軸上に中心をおいた半円の部分です。 その双曲的長さは、円弧の中心角
だけで定まります。 ですから、図のすべての赤い線分の長さは等しいのです。 中心PがX軸上のどこにあっても同じです。
上で得たユークリッド三角形は正しいでしようか？ なんだか技巧的で怪しい気がします。 もう少し調べてみましよう。 何よりも、平行線の公理がユークリッド化されていなければなりません。
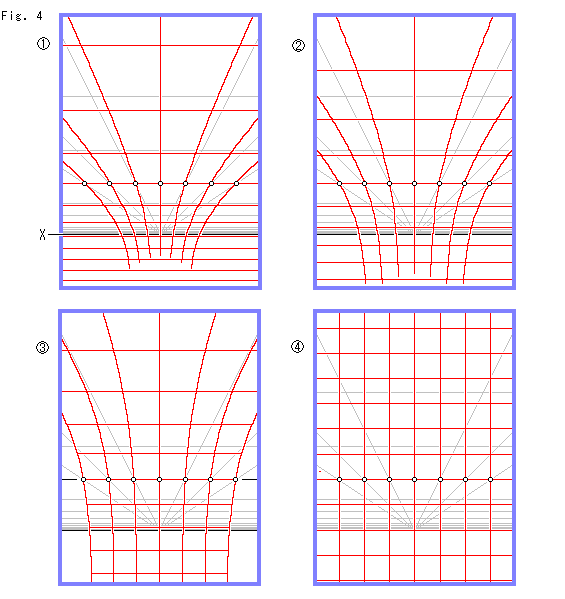
Fig.4をご覧ください。
上半平面を伸縮してユークリッド平面にする過程です。 灰色の線は上半平面を特徴づけたパターンです。 その水平な直線はY軸方向を双曲距離0.5ずつに刻んだものです。 X軸から出ている放射状の直線は、X軸方向を双曲距離0.5ずつに刻んだものです。 このパターンをユークリッド平面に適合するように連続的に変更します。 すると、から順に赤い曲線のように変化していきます。 印
の並んでいるところは基準線で、ここは動きません。 そこより上の横線は下へ降りてきます。 基準線より下の横線はさらに下へと降りていきます。 X軸より下へもいきます。 そして,とたどって、最後のでは完全に均質な直交格子になります。 X軸より下へも無限に広がっています。
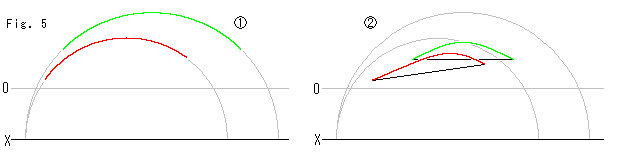
Fig.5をご覧ください。
双曲的に平行な線分をに引きます。 それを上で最後の赤い格子へいった手順に沿って変化させると、のようになります。 ユークリッド幾何の約束にしたがって曲線の両端を直線でむすんでみると、黒い線のようになって、それは一目で平行ではありまません。 どこか狂っているのでしようか？
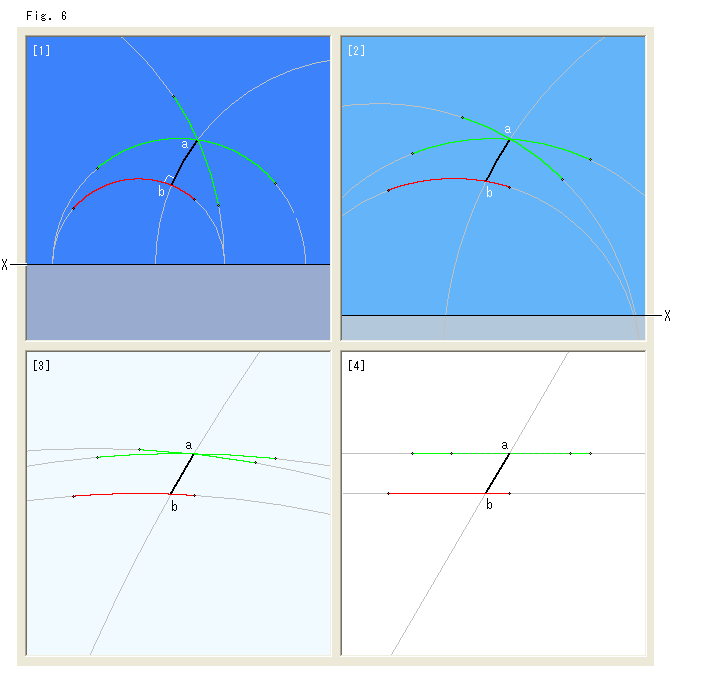
Fig.6をご覧ください。
もう一つ工夫してみます。
[1]: 上半平面に平行線を引きます。 赤い円弧を基準として、それに垂直な直線上の点aを共有する緑色の2本の平行線がああります。 平行線を置き去りにして、上半平面を上下左右均等に引き伸ばして拡大します。 ただし、平行な赤と緑の線分の長さは保っておきます。
[2]: 上半平面がわずかに拡大されたところです。 ずれたX軸が下に見えています。 平行な赤と緑の線分が、それらが乗っている半円とともに変形しています。 平行線間の黒い線分も、それにつれて変形しています。 地色を薄くなっているのは、上半平面が拡大されたことを表現しています。 平行線への双曲平面上にあることの効果が薄れてはじめているわけです。
[3]: 上半平面をどんどん拡大していったところです。 いま、初めの16倍になっています。 2本の緑色の平行線が一体になろうとしています。
[4]: 上半平面が無限に拡大してしまって、双曲的影響がなくなったところです。 双曲平行線がユークリッド平行線になって、緑色の平行線は1本になっています。 はじめに直角であったところは、図のような姿になっています。
これで、上半平面からユークリッド平面へ連続的に移れたといえないでしようか？ Ch.27で上半平面とユークリッド平面を行き来しました。 それは一方から他方へジャンプして移るものでしたが、平行線間の双曲距離とユークリッド距離は異なって描かれていました。 ところが、このFig.6では、そうはなっていません。 やはり、どこか間違っていますね。
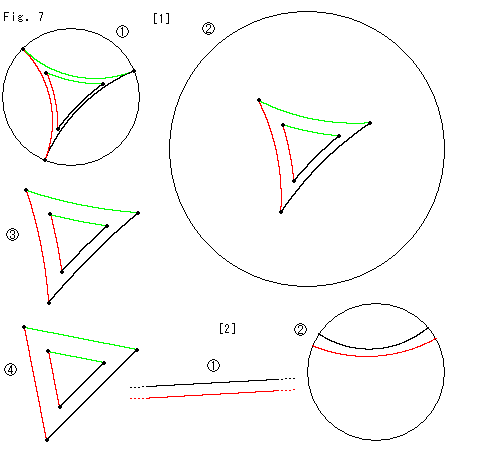
Fig.7をご覧ください。
上半平面は計算には便利です。 しかし、上下を感覚的にとらえるには都合のよいものではありません。 ポアンカレ円板で見てみましよう。
[1]: ポアンカレ円板にのように三角形を2つ描きます。 1つの三角形の頂点は、円板の周上にあります。 つまり、その三角形のどの2辺も双曲的に平行です。 もう1つの三角形の頂点は、大きい三角形の頂点を視覚的に相似縮小した点にとってあります。 これらの頂点を動かさずに、円板の半径を大きくしていきます。 相対的には、三角形が縮小していくことになります。 は、円板の半径を2倍にしたところです。 さらに円板を拡大していくと、のようになって、円板が無限に拡大したときはのようになります。 円板が無限に大きくなったということは、もう円板はポアンカレ円板ではなくて、ユークリッド平面に化しているとしてよいはずです。 もし円板の大きさを変えなければ、三角形は相対的に無限小になるのですが、そのようには考えていません。 いま三角形の3辺は真っ直ぐになっていて、どの2辺も平行ではありません。 ところが、2つの三角形の向かい合った2辺はでは双曲的平行ではありませんでしたが、このユークリッド平面ではユークリッド的平行になっています。
ユークリッド平面上の三角形の2辺の頂点が、もし無限遠にあるのなら、その2辺はで見るように双曲平面上で平行です。 ということは、私たちは無限大に描かれたポアンカレ円板上にいるとしてもよいわけですね。 同様に、無限大に描かれた上半平面に住んでいるとしてもよいのです。
[2]: ユークリッド平面からポアンカレ円板に移るときは、どうなるでしょうか。 はユークリッド平面上の平行線です。 [1]と逆の手順でポアンカレ円板にに移すと、のように平行でもなく、交わりもしません。 それは、の平行線はユークリッド平行線であって、無限遠でも交わらないものだとしたからです。
さて、こう見てくると、Fig.5は正しいといえそうです。 しかし、Fig.6の正否は、直ぐにはいえません。 ユークリッド平行線として描かれている[4]に無限遠が含まれていないからです。 はじめの上半平面で見れば、このユークリッド平行線とよんでいるものも、無限の彼方で交わっていると考えるべきでしよう。
無限遠を含めたユークリッド平面のモデルはありません。 Ch.1の半球のようなものを使っても、無限遠での様子を明言することはできません。
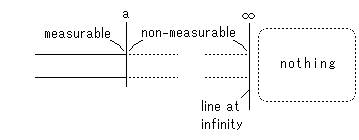
それよりも、Ch.8で「距離の測り方を定めておけば、"その先" は存在しないのだからから、無限の彼方は、想うことも描くこともできる」と述べました。 それにならって、右図のように考えましよう。 ユークリッド平面です。 ユークリッド平面は開平面で、ふつうは無限遠が除かれていますが、ここではそれを含めます。 ユークリッド平行線が無限遠まで伸びています。 aの線までは距離が測れる(measurable)ところです。 aはどこにでも設定でき、私たちのいる左の方からaまでの距離は無限大でない限り、いくらでも大きくとれます。 境界aを越えてたところは、距離の定義がない測れない(non-measurable)ところになっています。 けれども、ユークリッドの平行線の公理は生きています。 無限遠とかってに決めたところに無限遠直線(line at infinity)というものがあって、そこから先には何もありません(nothing)。 "そこから先" もありません。 "有無" もないのです。 いや、わからないのです。 しかし、平行線が交わっていないことだけは確かです。 無限遠までユークリッド平面が広がっているとしたのですから。
そうすると、Fig.6の[4]は正しいといえますね。 Fig.7の[2]のも、平行線の先端というものがあるとして、右図のように捉えればよいことになります。
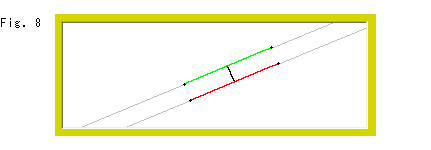
Fig.8をご覧ください。
赤と緑の線分は、ユークリッド平面上の平行線の部分です。 中央の黒い線分は、2線分の中点をむすんだもので、平行線に直交しています。 ユークリッド幾何では平行線と等距離線は同じですが、双曲幾何では別物です。 ですから、この2つの線分を上半平面へ移そうとするとき、平行線として扱うか等距離線として扱うかによって異なる結果となります。
議論はあとにして、描いてみましよう。
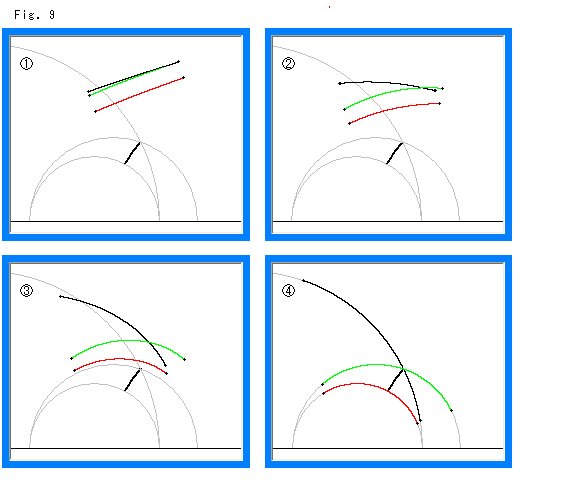
Fig.9をご覧ください。
上半平面上では直線は半円になることもあり、X軸に立つ垂線になることもあります。 ここでは半円になるとします。 そして、赤い線分がのっている直線を基線とします。 は、2線分がユークリッド平面から離れ始めた直後です。 緑色の1本の線分であったものが、黒と緑の2つになっています。 灰色の曲線は結果がわかっているので、下地に描いておいたものです。 中央の太くて黒い曲線は、基線である下側の半円に直交していて、ユークリッド平行線間の距離をそのまま双曲平行線間の距離としたものです。 双曲平行線では平行線間の距離は場所によって違うので、この黒い太線はその一つをとったものです。
ユークリッド平面から離れていくと、,のようになり、ユークリッド平面が上半平面になったときは、のように3つの半円の部分になります。 中央の黒い曲線から3つの線分の端までの距離はすべて等しくなっています。
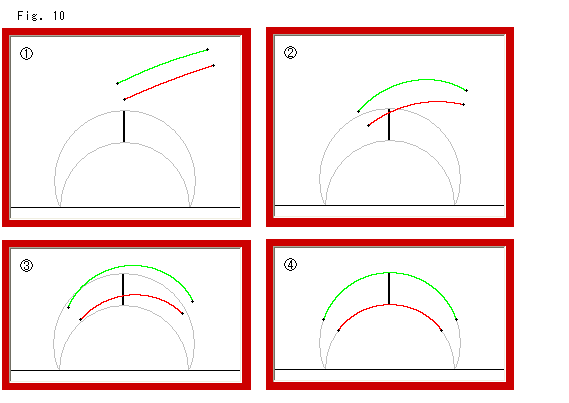
Fig.10をご覧ください。
こんどはユークリッド平行線を等距離線と見立てたもので、上と同じ要領で描いています。 灰色の曲線は、下側が基線にとった半円で、上側が等距離線です。
実は、Fig.9とFig.10はユークリッド幾何での計算式と双曲幾何での計算式を少しずつ差し換えていったものです。 それも簡単に、
として、kを0から1まで変化させただけです。
確かに、これで図形を円滑に変化させることができます。 しかし、それとともに平面が変わっていく様子を描くことができません。 各点の軌跡をとってみると、一直線に所要のところへと伸びているだけです。
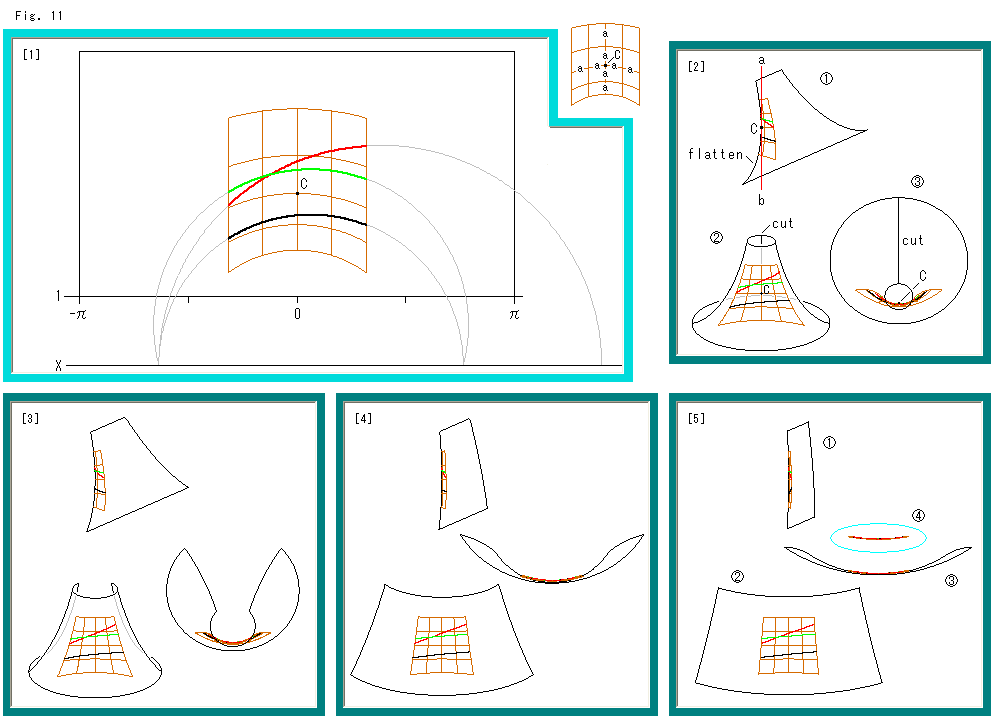
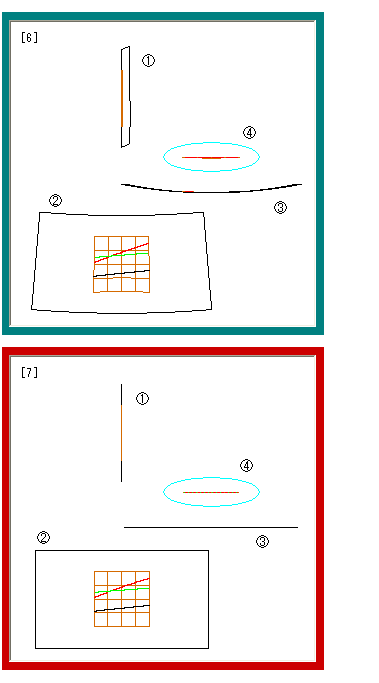
Fig.11をご覧ください。
式をすりかえることはしないで、擬球を利用します。 その擬球を平坦にすれば、ユークリッド平面になると見込んでやってみます。
[1]: 擬球上に測地線である直線を描くのは簡単ではないので、上半平面上に描いて、それを擬球に移します。 茶色の歪んで見える格子は、X軸に乗る半円の部分と垂直な線分からなっています。 つまり、双曲直線でできています。 点Cは格子の中心です。 枠外の右上に示すように、点Cを通る垂直線上とアーチ型の横線上の格子点だけが等間隔aになっています。 この2線分以外のところでは、どのマス目の辺もaと異なる長さです。
縦方向の1から上にある長方形が、対応させる擬球の範囲です。 その内側の格子面に注目します。 黒い線分を基準として、赤い線分は平行で、緑色の線分は等距離線です。
[2]: 格子面を擬球に移したところです。 [1]の長方形に合わせて擬球の尻尾を切り落としています。 の赤い直線abは、格子の中心Cにおける接平面です。 その接平面が垂直となるように擬球を傾けます。 擬球を傾けたままで格子面を真正面に向けると、のようになっています。 は、それを真上から見たものです。
この擬球を切り(cut)裂いて、同時に朝顔形のスカートを平坦に(flatten)していきます。
[3], [4]: 切った擬球を平たく広げていきます。
[5]: だいぶん平たくなりました。 上から見たでは格子のところが見ずらいですね。 は、そこだけを取り出したものがです。
[6]: さらに擬球を押し広げていきます。
[7]: ついに擬球は長方形の平面になりました。 ユークリッド平面です。 3本の双曲直線がユークリッド直線になっています。 そこでは、黒と赤の直線は平行ではありません。 しかし、黒と緑の直線は平行です。 それは等距離線でもあります。
まてよ。 どうもおかしい。
復習してみましよう。 平行線は交わるという双曲幾何の公理と、平行線は交わらないというユークリッド幾何の公理があります。 この2つの公理の中間をたどって一方から他方へ移ろうとしているわけです。 ところが、2つの公理の中間的な公理はありません。 でも、計量とか曲率に目をとめると、中間的な計量や中間的な曲率があります。 それを想って私たちがこころみたのは、双曲平面をユークリッド平面へ連続的に変えることでした。 それは、
双曲平面のモデル上に三角形がある。 三角形はそのままにしておいて、モデル平面を拡大していく。
すると終には、三角形を含む付近はユークリッド平面に変わり、双曲三角形がユークリッド三角形になる。
ところが、平行線では同様に扱えない。 双曲モデル平面を（その上の平行線はそのままにしておいて）いくら拡大しても、平行線全体を含む付近といったものはない。
しかし、平行線の部分だけをとれば、その付近はユークリッド平面に変わる。 平行線の無限の先の方については、別に見ることにする。
双曲モデル平面を無限大に拡大したとき、その無限遠においても双曲モデル平面であることに変わりはない。 けれども、平行線の部分の付近と同様に、いたるところがユークリッド平面になっているとする。 全体の性質は部分のそれと同じという考えである。
双曲平面にもユークリッド平面にも、実際には無限遠が含まれていないので、この考えは無茶ではない。
といったものでした。 やはり、スッキリしないところがいくつもありますね。
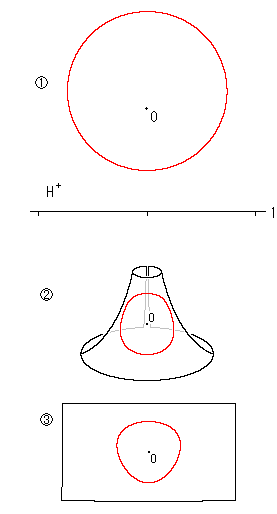
それに、作図をまちがっているかもしれません。 というのは、右図のようになるからです。 上半平面上のOを中心とする双曲円が、それを擬球に移して、その擬球を切り開いて平坦にした平面では卵形になってしまいます。 それは当然といえば当然だともいえそうですすね。 実は、擬球を連続的に変形する数式は、私たちが適当に作ったものです。 正否の証明はできていません。 ですから、キッチリ確かめるには、やわらかい擬球面を実際に作って平坦にしてみるほかありません。 擬球面の部分は偏った鞍形です。 その擬球面のどの小さな部分を切り取っても、伸縮させずに曲げるだけで他の場所に等長的におくことができるといわれています。 "等長的"の意味も確かめたいですね。 私たちの場合には伸縮もともないます。 いつか実験してみます。