第２部 双曲的非ユークリッドの世界
Ch.33 直角正多角形 
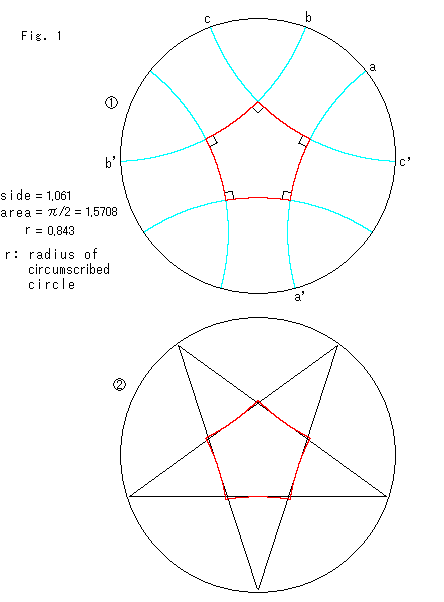
双曲幾何では四隅が直角である正方形は存在しません。 しかし、頂点が5個以上の多角形なら、すべての内角を直角にすることができます。
Fig.1はポアンカレ円板の中心に直角正五角形を描いたものです。
: この直角正五角形の面積(area)は、ぴったり直角のラヂアンでの値になっています。 rは外接円の半径(radius of circumscribed circle)です。 辺(side)は1より大きいですけれども、この半径は1より小です。
水色の直線(円弧)は各辺の延長線です。 2本の直線aa'とbb'は超平行になっているので、それらの共通垂線は1本しかありません。 それが直線cc'です。 このことから、直角正五角形でタイル張りはできないことがわかります。
: ポアンカレ円板上では辺が円弧に描かれているので、その辺の中点を通るふつうの接線を引くことができます。 こころみにやってみると、円板にはまった星形のパターンになりました。 しかし、よく見ると、星形の先端は円板の縁に達していません。
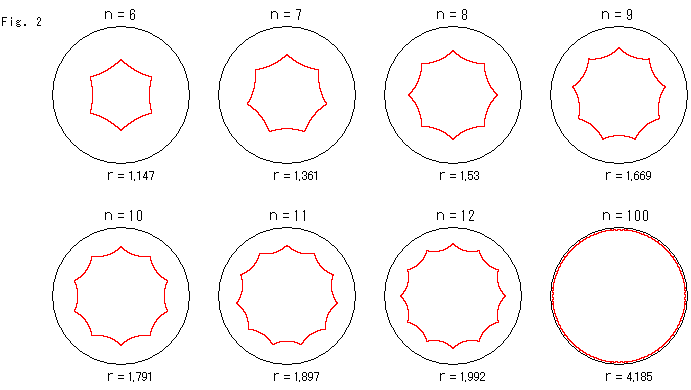
上のFig.2をご覧ください。
直角正多角形の辺の数nを増やしていったものです。 辺の数nが増すと、少しずつ大きくなっています。 しかし、それは目で見てのことです。 実際の双曲的大きさは、外接円の双曲半径rで表しています。
Fig.3をご覧ください。
直角正多角形の全部を一度に描いてみると、のようになります。 水色の円は双曲半径1の円で、観察の便に添えたものです。
直角正100角形は円板の縁に近くにあるので、よく見えませんが、拡大してみるとのようになっています。 内角のすべてが、ちゃんと直角になっているのがわかります。
頂点の1つを円板の中心Oに固定して辺の数nを増やしていくと、Fig.4のようになります。 この場合、辺の長さが直線状のところと円弧のところでは違うので、正多角形ではありません。 しかし、直角多角形ですので面積はFig.3のと変わりありません。 円板の縁に触れそうになっているのは、直角100角形です。
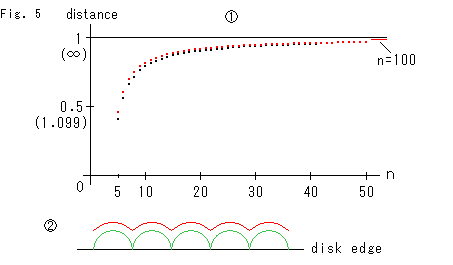
Fig.5をご覧ください。
は、上のFig.4の要領で直角多角形を沢山つくっていったときの、辺の数nと中心Oから円弧の辺までの距離(distance)の関係をプロットしたものです。 括弧( )内は双曲距離です。 赤い点は中心Oにもっとも近い円弧上の点までの距離（直線状のところと同じ）で、黒い点は頂点までの距離です。 辺の数nが増していく右の方では、赤い点と黒い点が1つになったように見えますが、両者が重なることはけっしてありません。 右上に赤い線で示してあるのは、直角100角形のものです。
は、辺の数nを極度に増やしたときの円板の縁(disk edge)のあたりの様子を拡大したものです。 赤い円弧は直角多角形の辺の一部です。 ウンと拡大してあるので、円板の周がほぼ直線になっています。 緑色の円弧は黒い直線状の上に中心を置いて赤い円弧と同じ間隔にならべた半円です。 赤と緑の円弧の中心はほぼ同じで、両者はほとんど同心円上にあります。
さて、直角多角形の辺の数nを無限に多くすれば、その頂点を円板の縁に触れさせることができるでしようか？
それは不可能です。 もし直角多角形の頂点が円板の縁に達したとしたら、緑色の半円のように内角がゼロになってしまって、直角多角形ではなくなってしまいます。 どんな多角形の場合でも同様です。
モデル円板は開円板であることを思い出してください。 直角多角形の辺の数nはいくらでも大きくすることはできますが、無限大にはできないのです。
[前章] [次章] [目次]