第２部 双曲的非ユークリッドの世界
Ch.34 十二面体 
これまで、双曲的非ユークリッドの世界の平面(２次元)のものだけを扱ってきました。 ３次元の世界ではどうなっているのでしょうか。
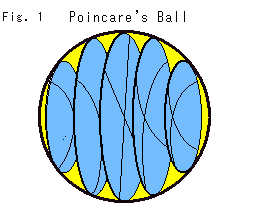
ここでは、ポアンカレの円板モデルを3次元に拡張したポアンカレ球体モデルで考えます。 むろん、球体は開空間で、その双曲半径は無限大です。
Fig.1をご覧ください。 球体モデルを垂直にスライスしたものです。 お皿や椀形に見える双曲平面が描かれています。 凹んで見えていても、双曲的平面です。 そして、どの平面の縁も球体の表面に垂直です。
見て取りやすくすために、図では平面を得るのに球体を同じ方向に切っています。 むろん、どの方向に椀状に切っても双曲平面になります。
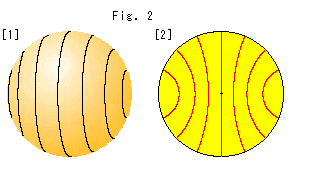
Fig.2をご覧ください。
[1]は、球体の外観です。 黒い線は、Fig.1の凹んだ平面の縁です。
[2]は、球体を中心で切った断面です。 赤い線は、平面の断面です。
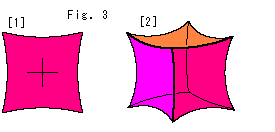
Fig.3をご覧ください。
[1]は、ポアンカレの円板内に描かれた正方形です。 むろん内角は90
より小です。 これでタイル張りすることはできません。
[2]は、球体内の立方体です。 隅が尖っています。 球体内にこれをレンガのように積むことはできません。
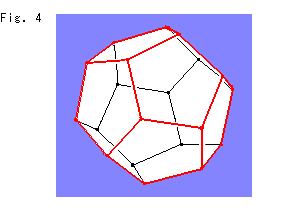
Fig.4は、ふつうの正十二面体です。 12個の五角形、20個の頂点、30本の辺からなっていて、面と面のなす角（辺角, dihedral angle）は116.565です。 そして、どの面にも反対側に、10分の1回転して向かい合っている平行な面（逆立ちした正五角形）があります。 球体の中をこれで隙間なく埋め尽くしてみます。 ちょっとイメージしにくいですが、双曲的非ユークリッドの世界では、それができるのです。 ブロック積みとか3Dタイル張りといってもよいでしょう。
仕掛けはこうです。
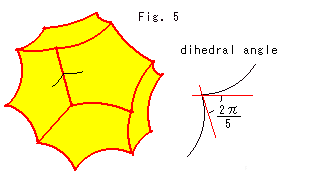
Fig.5をご覧ください。 正十二面体を球体の中に入れると、頂点が尖り、辺角が小さくなります。 正十二面体を球体モデルの真中に置いて伸縮すると、すべての辺角をちょうど 2
/5(=72)にすることができます。 この大きさの正十二面体を使えば、どの１辺のぐるりにも5つの正十二面体をきっちり並べていくことができます。 いうまでもなく、球体を完全に埋め尽くすには、無限個の正十二面体が要ります。
辺角を90にすれば、1辺のぐるりに４個並べられる直角12面体とよばれているものができます。 辺角が60なら、1辺のぐるりに6個並べられます。 この場合は理想十二面体というものになり、すべての辺が球体の表面へと伸びています。
下のFig.6は、3Dタイル張りです。 辺角72の正十二面体の1
つ(空色)を球体の中心に置いてベースにし、その周囲に正十二面体をつぎつぎと3層(shell)まで積み上げていったものです。 赤い第１層に12個、白い第２層に144個、青い第３層に1728個と積み上げています。 図で見えているのは、およそ、その半分です。 図の[1]〜[3]は、球体の中心に立って周囲を見たものです。
[1]は、頭上を見上げたものです。
[2]は、前方の様子です。
[3]は、右の方を見渡したものです。 左の方は、これと対照的に同じです。
[4]は、球体の外側から正十二面体の1つを見たものです。
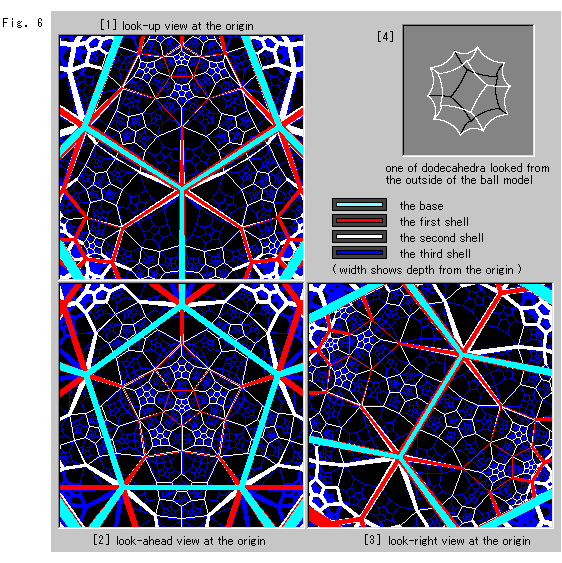
Fig.7は、辺角60の理想十二面体です。 辺が曲がって見ます。 しかし、球体モデルの中へ（身も心も）入って眺めると、すべての辺は真っ直ぐです。
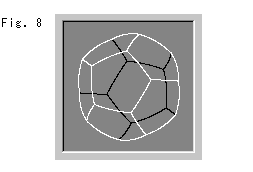
Fig.8をご覧下さい。 もし、球体内の住民が、球体の外側（ユークリッド界）にある私たちのふつうの正十二面体を見ることができるとしたら、たぶん図のように、膨らんで見えるでしょう。
右のFig.9をご覧下さい。 球体の内側で、積み上げた層から十分離れて眺めると、前方の景色は図のようになっています。
Fig.10は、ガンによる芸術的な作品の直角十二面体の3Dタイル張りです。 なんと、魅惑的ではありませんか。 Fig.6と見比べてください。 よく似ていますが、同じではありません。
Webには、ログマンによる動く3Dタイルもあります。
[前章] [次章] [目次]