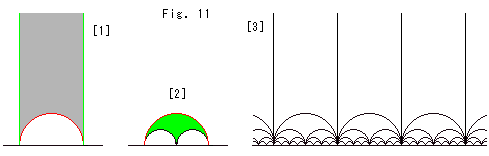第２部 双曲的非ユークリッドの世界
Ch.35 理想四面体 
理想正四面体で3Dタイル張りをすると、どんなになるでしょうか。 ここでのことは、第３部の８字ノットの話しの後半につながってきます。
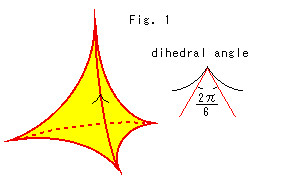
Fig.1をご覧下さい。
理想正四面体のすべての頂点は、球体モデルの表面へと伸びています。 ふつうの正四面体の辺角は70.517
でが、ポアンカレ球体モデルの中では辺角がちょうど2
/6(=60)になっています。 正四面体6個で1つの辺を完全に囲むことができます。 球体モデルの中にきっちり敷き詰めていくことのできる正四面体は、これ以外にありません。 球体の中では正四面体の辺角は70.517より小なので、正十二面体のように大きさを変えて、いろいろな辺角のものを選ぶことができないからです。
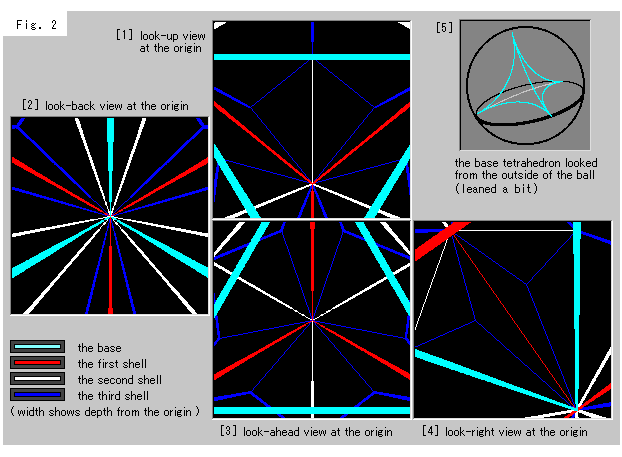
下のFig.2をご覧下さい。 [1]〜[4]は、球体の中心からの眺めです。 手順は、十二面体のと同じです。 赤が第1層、白が第2層、青が第3層となっています。
[1]は、頭上を見たものです。
[2]は、前面の眺めです。
[3]は、後ろの様子です。
[4]は、右側です。 左側は対称的に同じです。
[5]は、球体の外側から理想正四面体の1つを見たものです。（見易くするために、ちょっと傾けてあります｡）
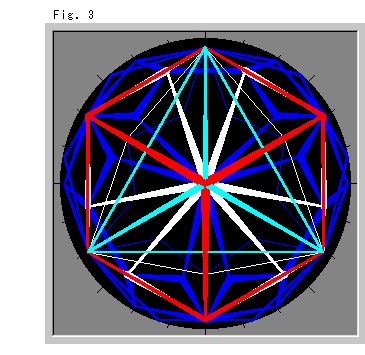
右のFig.3をご覧ください。 球体の全体ですが、あたかも観察者がその中にいるように描かれています。 つまり、辺のすべてが真っ直ぐです。
理想頂点について：
理想頂点は、頂点が無限遠へと伸びて行っているもののことです。 しかし、すべてのモデルは開いているので、理想頂点は、実際には存在しないフィクションだといわれています。 そうだとすると、あの射影幾何の無限遠直線の辺りの様子はどう考えたらよいのでしようか？
私たちは、そのときの都合次第で、頂点の存否を選ぶことにします。 そして、単に頂点といっていても、仮想的なものを指している場合があることに心しておきましよう。 もっとも、たいていは気にしなくても済みます。
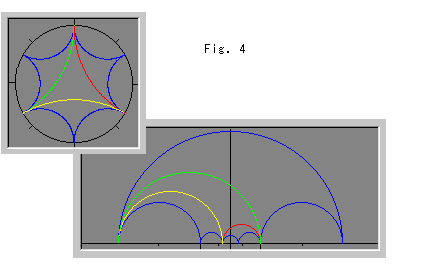
Fig.4をご覧ください。 理想正四面体の代わりに理想三角形を使って、ポアンカレ円板(左上)と上半平面(右下)で見てみます。 ポアンカレ円板上の青い曲線は、中央の辺が赤黄緑の三角形を、その各辺に関して反転したものです。 3Dタイル張りでのベースに相当するのが中央の三角形で、第1層に相当するのが青い3つの三角形です。 上半平面上の曲線は、ポアンカレ円板上の曲線と対応しています。
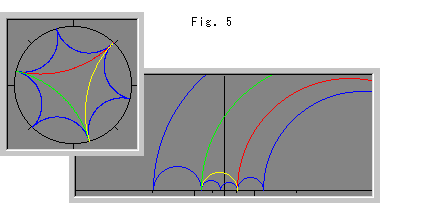
Fig.5は、ポアンカレ円板上で三角形を少し回転してみたものです。 上半平面上の三角形が大きく変化して見えます。
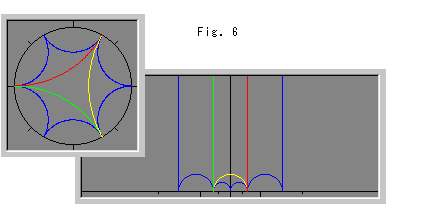
Fig.6では、上半平面上の各三角形の2辺が上方の無限遠へ伸びています。
さて、3Dです。
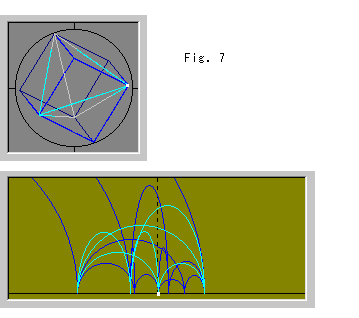
Fig.7をご覧ください。 上がポアンカレの球体モデルで、下が上半空間です。 球体は、理想四面体と立方体をかかえています。 立方体はベースの四面体と第1層の4つの四面体からなっています。 これらの理想四面体は、きっちり立方体を形成しています。 各辺は、球体内部でみているものとして、直線で描いています。暗い色のところは、球体の中心を通る垂直な平面(カーテン)の向こう側です。
上半空間というのは、上半平面のX軸を水平な平面にしただけのものです。 白いスポットが対応している頂点です。 見にくいですが、空色のアーチが6本、青いアーチが12本あります。
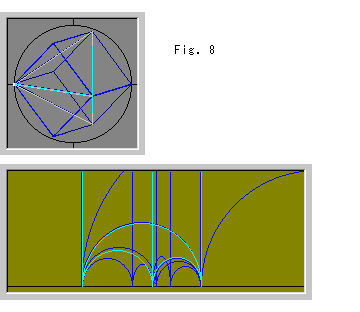
Fig.8をご覧ください。 ポアンカレの球体の理想四面体の位置を変えてみたものです。 この場合、上半空間には、白いスポットの対応点が見当たりませんが、上方の無限遠へ行ってしまっています。
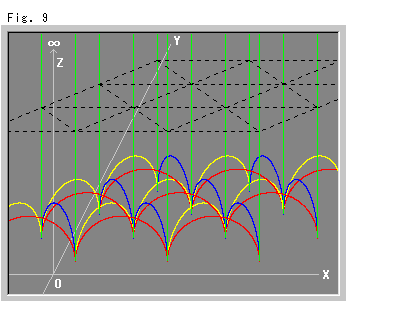
Fig.9は、ポアンカレの上半空間に理想正四面体を敷き並べて行っているところです。 それぞれが、球面の底面をもった三角柱として描かれています。 理想正四面体辺は、３本が赤青黄の円弧で、残り３本が緑色の直線です。 黒い破線のネットは、観察用のもです。 理想四面体には頂点がないとすると、下方へ向かっている辺は、床(Z=0)から浮いていています(Z>0)。
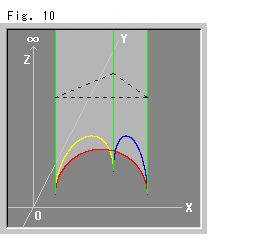
Fig.10は、見やすくするために、理想正四面体をうすく着色して１つだけ描いたものです。
下のFig.11をご覧ください。 Fig.10の理想正四面体を反転させると、三角柱の下側の空いたところに理想正四面体を詰めることができます。 立体図ではかえって見にくいので、理想正四面体を理想正三角形で代用して、上半平面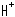
を使います。
[1]は、上半平面上の理想正三角形の1つです。
[2]は、[1]の下側に密着した理想正三角形です。
[3]は、[1]の下へどんどんはめ込んでいた理想正三角形です。 これが、3Dタイル張りに相当する2次元のタイル張りです。
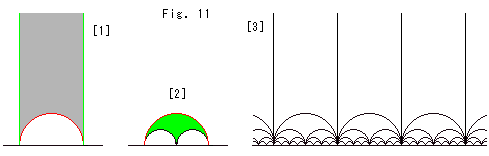
Webに、とても美しい理想多面体があります。
[前章] [次章] [目次]
(次章は第３部)