第３部 射影幾何から双曲幾何へ
Ch.36 射影幾何 (1) 
どうしても、射影幾何の力をかりねばならなくなりました。 リーマンの考え方では、意図して計量とか曲率を選ぶことによって、双曲幾何を得るものでした。 そこには、双曲幾何が生まれる必然性が感じられません。 一方、ロバチェフスキーの方法には必然性があるようですが、どうしても神秘的な要素がつきまといます。
射影幾何からは、自然に双曲幾何が出現するといわれています。 そして、無限を有限と区別して特別扱いしなくてよいそうです。 本当でしょうか？ 一体、射影幾何ってどんなものですか。 まずは、それを見ていきましよう。
ユークリッドの世界にもどって、当面、双曲的非ユークリッドの世界のことは忘れてください。 そして、いつものように色々描いて、無限を見ることをこころみます。
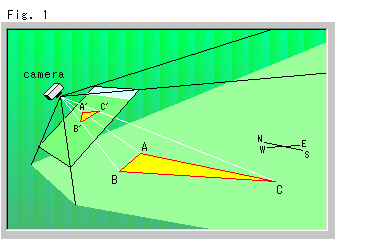
Fig.1をご覧下さい。
カメラは射影の中心で、地面の三角形ABCを写しているところです。 この地面は完全な平面(地球は丸くない)としたものです。 明るい緑色のところがカメラから見れる部分で、カメラから出ている黒い射線がファインダー内に入る立体的な領域(四角錐)を示しています。 その射線にはめられている四角い板は、私たちがカメラを通して眺められることのできるものを表わしています。 四角い板をパネルスクリーンとよんでおくことにします。 地面の三角形ABCの写真は、パネルスクリーン上に三角形A'B'C'として得られます。 白い直線は三角形の頂点の射線です。
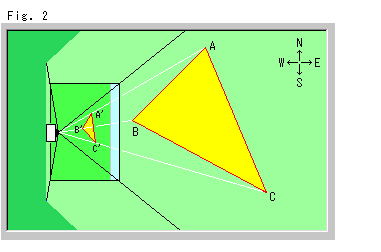
Fig.2は、Fig.1の状況を真上から見たみたものです。 地面の三角形ABCの形が正しく描かれています。 東西南北の矢印も絵のとおりです。 しかし、パネルスクリーンはまだ傾いているので、三角形A'B'C'も傾いたままです。
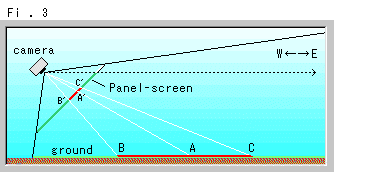
Fig.3は、横から見たFig.1の状況です。 黒い点線は、カメラから見た地平線の方向を指しています。 下のまだらな茶色いところは、地面(ground)の断面です。 パネルスクリーン(Pannel-screen)も三角形ABCとA'B'C'も真横から見ているので、直線状に描かれています。
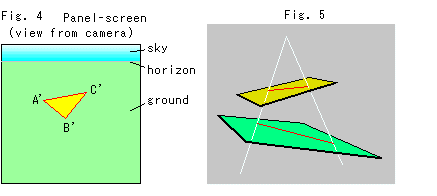
Fig.4は、三角形A'B'C'の描かれたパネルスクリーンをその正面から見たものです。 上の方は空(sky)で、緑色が地面(ground)、その境界が地平線(horizon)です。 三角形A'B'C'の形と大きさ(内角と辺の長さ)は、Fig.3の実際の三角形ABCとは異なっています。 しかし、三角形であることに変わりはありません。 つまり、直線は直線として保存されるということです。
Fig.5は、直線が射影変換によって変わらないことを説明しているものです。 見れば、明らかですね。
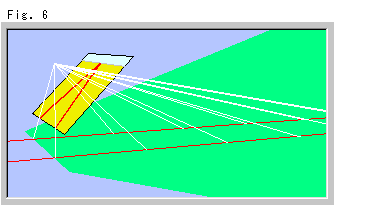
Fig.6は、平行線の射影です。 見やすくするために、カメラなどを省いて、パネルスクリーンの地色を黄色にしています。 平行線が地平線のところでたがいに出会っていて、そこが端点のように見えます。
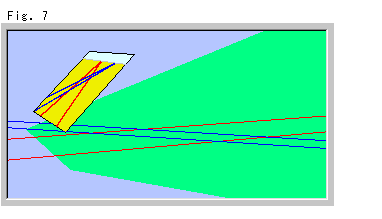
Fig.7をご覧ください。 2組の平行線を地面に描いて、パネルスクリーンに射影しました。 白い射線は省いています。 青い平行線も地平線のところでたがいに出会っています。
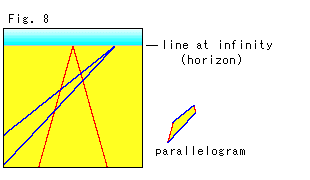
Fig.8は、パネルスクリーン上の2組の平行線です。 右下のは、平行四辺形(parallelogram)だけを取り出したものです。
数学者は、パネルスクリーン上の地平線を無限遠直線(line at infinity)とよんでいます。 しかし、そんな線が実際に存在するわけではありません。 この名前は、まことに不適切です。 初めて学ぶものを混乱させます。 無限に遠くにある線ではありません。 空と地面の境界としてパネルスクリーン上に捉えることができるだけです。 いいかえれば、
無限遠直線は人工製品です。
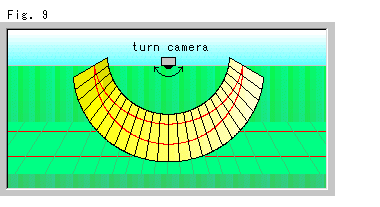
Fig.9は、沢山の短冊形のパネルスクリーンをつかった180
撮影です。 連ねたパネルスクリーンは、半円筒になっています。 これで平行線全体の写真をとることができます。 地面の平行線は鉄道線路のように見えますが、パネルスクリーン上の平行線はそうではありません。
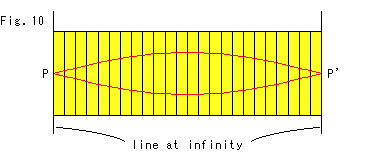
Fig.10は、Fig.9のパネルスクリーンを平面に広げたものです。 点PとP'が無限遠直線(地平線)上にあります。 連ねたパネルスクリーンは、平行線全体をパノラマ風に見るのによいですね。 しかし、間隔の大きい平行線を見るには具合がよくありません。 また、異なる方向の直線をカバーすることはできません。
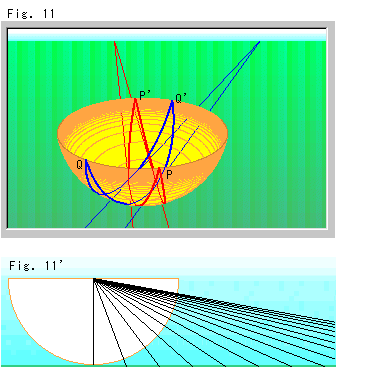
Fig.11は、半球面上の2組みの平行線です。 それは、地面からパネルスクリーンのかわりに半球面へ射影したものです。 半球面の中心が射影の中心です。 半球面は、無数の微小なパネルスクリーン(接平面)からなっていると考えられます。 半球面の縁(赤道)は、いま無限遠直線です。 曲がって見えますけれど、直線といいます。
Fig.11'は、半球面の中心を垂直に切った断面です。 黒い直線は、地面を等間隔にとった射線です。 左側と射線が水平に近いところは、省いています。
さて、この半球面を平面だとみなして、そこでの幾何を考えてみましよう。 当然、大円が直線ということになります。 ところが、問題があります。 ユークリッド幾何では、2点を通る直線は1本に限られるのです。 2本の赤い直線が2点P,P'に達しています。 青い2本の直線もどうように2点Q,Q'にとどいています。 これでは、いままでの幾何となじめません。 リーマンが、それを解決してくれました。 点Pと点P'を同一視し、点Qと点Q'を同一視すれば済むのです。
わかりました。 ともかく、受け入れましよう。 でも、それはどんな平面ですか？ どのようにして、点Pと点P'を1点に結びつけ、同時に点Qと点Q'を1につなぐのですか。 半球のふち全体がそのようになっていなければならないのですが、それは物理的に不可能です。 しかし、私たち人間は、それを空想することができます。 それが射影平面です。 「空想で幾何の話をするとは、けしからん」という声も聞こえますが、ともかく進みましよう。 なにしろ、半球面の縁は無限の彼方を取り込んだところですから。
[前章] [次章] [目次]