第3部 射影幾何から双曲幾何へ
Ch.37 メビウスの帯 (1) 
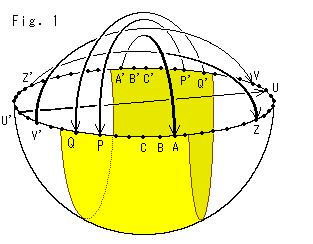
球の直径の両端を対心点というのですが、半球面の縁には、無数の対心点があります。 無限の彼方を含む平面を射影によって取り込んだ半球面は、対心点のすべてを同一視したものでなければなりません。 それは、半球面の下に広がっている平面自体の四方八方の無限の彼方が、対心点のようになっているのだということです。 そのように捉えた平面が射影平面です。
Fig.1をご覧ください。
射影平面のモデルとしての半球面を実際に作ることはできません。 けれども、図の黄色いところだけを取り出して、部分的なものを作るなら簡単です。 それが、よく知られているメビウスの帯です。 ここでは、実物をいじくるようにして、その性質を素朴に捉えていきます。
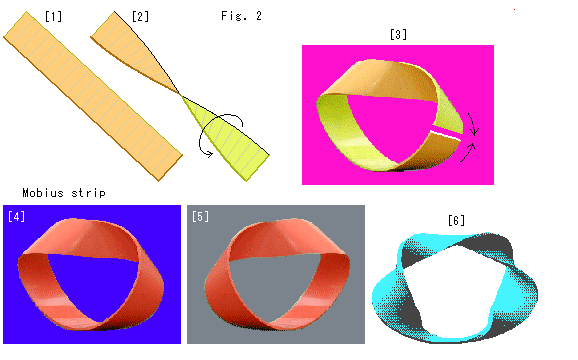
Fig.2をご覧ください。
メビウスの帯の作り方はご存知でしようが、まず、それを見ていきます。
[1]: 紙かゴム板を短冊状に切ります。 両端以外なら少々ゆがんでいてもかまいません。
[2]: 半分(180 )ねじります。
)ねじります。
[3]: 一端を他端の方に曲げます。 まだ、表裏をはっきり区別できます。
[4]: 両端をつなぎます。 この瞬間、私たちは、どちらが表か裏かをいうことができなくなります。 そして、縁も1つになります。 これがメビウスの帯です。 それは、単側で、向きつけ不能といわれているものです。
[5]: [2]のように左捻りせずに、右捻りして作ったものです。 これもメビウスの帯ですが、[4]と重ね合わせることはできません。
[6]: 短冊の捻り方は、180 の奇数倍なら何回ひねってもかまいません。 この図は3回ひねったものです。 このようにしてもよいわないわけですが、1回だけ捩ったもので考えていきます。
の奇数倍なら何回ひねってもかまいません。 この図は3回ひねったものです。 このようにしてもよいわないわけですが、1回だけ捩ったもので考えていきます。
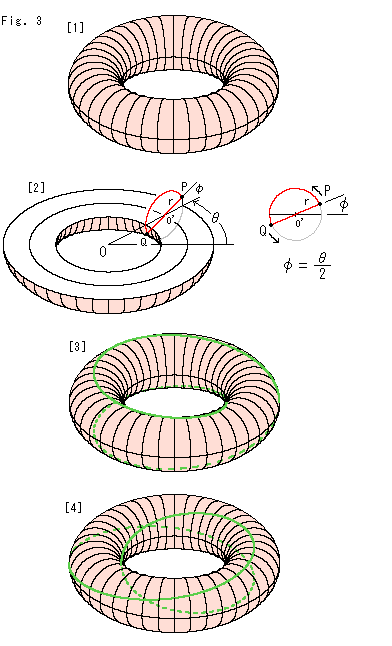 Fig.3をご覧ください。
Fig.3をご覧ください。
メビウスの帯は、Fig.2のような均整のとれた芸術的な形のものでなくてもかまいません。 要は、表裏の区別がないループ状のものであればよいのです。 計算がしやすくて、メビウスの帯の面上の様子を見るのに都合のよいものがトーラスから得られます。
[1]: ふつうにトーラスというときは、図のようなドーナツ形の面を指します。 それは式で
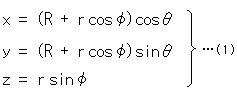
と表わされます。 rとRを一定にしておいて、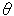 と
と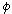 を変化させると、点Pが動きます。 点Pをトーラスの表面のどこへでももっていくことができます。 つまり、この式(1)はトーラスの表面を表わしているのです。
を変化させると、点Pが動きます。 点Pをトーラスの表面のどこへでももっていくことができます。 つまり、この式(1)はトーラスの表面を表わしているのです。
[2]: この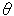 と
と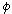 を
を
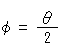 と関係づけて、点Pの動く道を定めます。 すると、
と関係づけて、点Pの動く道を定めます。 すると、
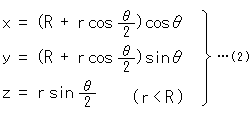
となります。 つまり、小さい円o'が大きい円Oを2周すると、点Pが小さい円o'上を1周するのです。 PQは円o'の直径です。 この式(2)は、rが一定なのでメビウスの帯の縁を表していますが、Rより小さい一定の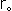 をとって
をとって
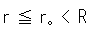
として r を変数にすると、式(2)はメビウスの帯の面を表します。 トーラスの環が空洞のチューブでなく中の詰まったものをソリッドトーラスというのですが、そんなので考えています。
[3]: 緑色の曲線は点Pの軌跡です。 点線は、見えない側を点Pが這っているところです。 点Pが実線上にあるときは点Qが点線上にあり、点Pが点線上にあるときは点Qが実線上にあります。
[4]: 見やすいように[3]をすこし回してみたものです。
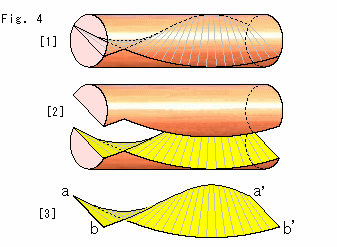
Fig.4をご覧ください。
[1]: メビウスの帯がソリッドトーラスの中にどのように入っているかを見るために、トーラスのループを切って、短い円柱にしてみたものです。 この円柱は、メビウスの帯を境に分離できます。 両端は、ループとして同一視する約束です。
[2]: 上の部分を取りはずそうとしているところです。
[3]: 下側も取り去って、切口だけを残したものです。 aとa'、bとb'がつながれてループになったものがソリッドトーラスの中にあるわけです。
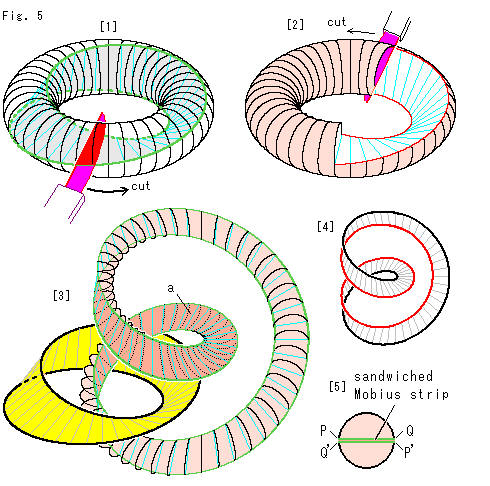 Fig.5をご覧ください。
Fig.5をご覧ください。
環状のままのソリッドトーラスからメビウスの帯を取り出します。
[1]: ソリッドソリッドトーラスの中にメビウスの帯が潜んでいいます。 赤いナイフを突き刺して、図のように緑色の曲線に沿ってトーラスを切ります。 しかし、このように切ってもトーラスは二分されません。 メビウスの帯を物理的に得るには、切口を残して周囲を削るか溶かすほかないのです。
式(2)はメビウスの帯とソリッドトーラスとの関係との関係を含んでいますが、そこから取り出すといった考え方については何もいっていません。 また、空想するだけなら、切らなくてもメビウスの帯を取り出すことはできます。 しかし、物理的にどうなのか、ちょっと見ておきましよう。
[2]: 切っている途中です。 メビウスの帯だけを残して、他を捨てながら進めています。 こうして赤いナイフを2周させるとメビウスの帯を切り出すことができます。
[3]: ソリッドトーラスはゴム製だとします。 そして、何も捨てないで切った場合です。 ソリッドトーラスは、黄色いメビウスの帯とそれに絡んだ長いループに分離されます。 こい色の面aはメビウスの帯に接していた側です。 絡んだループの長さはメビウスの帯の2倍になっています。 メビウスの帯だけを手に入れることは、この絡んだ長いループを切断しないかぎり、できません。
[4]: 長いループの面aだけをとって、その縁を赤と黒に染めたものです。 このように染め分けできるので、表裏の区別ができる面です。 メビウスの帯は単側なのに、どうしてでしよう?
[5]: ソリッドトーラスを赤いナイフで切りました。 それはメビウスの帯を2周して完了します。 上側PQから切っていくと一周して下側P'Q'へ回わるので、もう一周切らねばなりません。 それで、絡んだループの長さが2倍になっているのです。 そして赤いナイフは、この間に360 のスクリュー回転をします。
のスクリュー回転をします。
この360 というのは、ナイフの刻々に変わる進行方向を軸として見たものです。 そして、ナイフ自体はトーラスの穴の周りを2回めぐっています。 天体の自転と公転のような関係です。
というのは、ナイフの刻々に変わる進行方向を軸として見たものです。 そして、ナイフ自体はトーラスの穴の周りを2回めぐっています。 天体の自転と公転のような関係です。
メビウスの帯は180 捻じられたものだといわれおり、実際に短冊を180
捻じられたものだといわれおり、実際に短冊を180 捻じてつくることができます。 しかし、メビウスの帯の面をなぞってみると、180
捻じてつくることができます。 しかし、メビウスの帯の面をなぞってみると、180 であるのは(部分ぶぶんで見た)片側を1周だけしてのことです。 2周して面全体を舐めていけば、360
であるのは(部分ぶぶんで見た)片側を1周だけしてのことです。 2周して面全体を舐めていけば、360 になります。
になります。
そして、表裏がない面に密着している面には表裏があるということです。 むろん、それは密着した面を剥がした後での話しです。 密着したままでは、表裏があっても、その一方しか見ることはできません。
**************************************************
メビウスの帯の性質を知るために、その面に作図したり、メビウスの帯そのものをいじくったり、面に物を置くなど、いろいろとやってみます。 式(2)を利用したメビウスの帯で描きます。
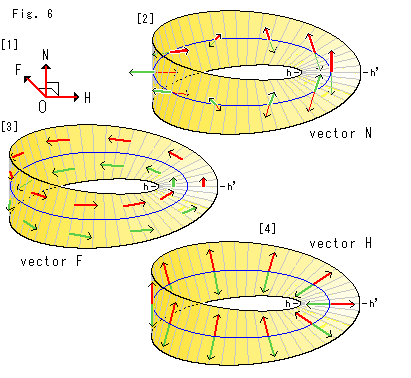 Fig.6をご覧ください。
Fig.6をご覧ください。
まず、3種類のベクトルを描いてみます。
[1]: たがいに直交する3つの矢線ベクトルにN,H,Fと名前をつけておきます。 メビウスの帯の面にこれらのベクトルを立てていきます。 ベクトルNはの法線ベクトルです。 ベクトルHとFは接ベクトルで、ベクトルHはメビウスの帯を横切る方向に、ベクトルFはメビウスの帯をめぐる前進方向にとります。 メビウスの帯をめぐる1周めを赤色に、2周めを緑色にと色分けします。
[2]: メビウスの帯を横切ったhh'をスタートラインにとって、青いセンターラインに沿って左回りに法線ベクトルNを立てていったものです。 法線ベクトルNは1周すると逆向きになり、もう1周すると元に戻ります。 そして、同じ点で赤と緑のベクトルが背中合わせになっています。 とうぜん、面の向きをいうことはできません。 スタートラインをどこにとっても変わりません。
[3]: 前方を向いた接ベクトルFです。 コースは青いセンターラインから一定距離のところです。 赤いベクトルFは一周してスタートラインもどると、矢線の向きは変わりませんが、センターラインの反対側にきます。 コースは1本でセンターラインを横切ってはいません。 このベクトルも、もう1周すると元に戻ります。
[4]: もう一つの接ベクトルHです。 2周めの緑色のベクトルは、[1]と同様に赤いベクトルと背中合わせになって、反対方向を向いています。 メビウスの帯はループになっていますが、その内側と外側も区別がないのでしようか?
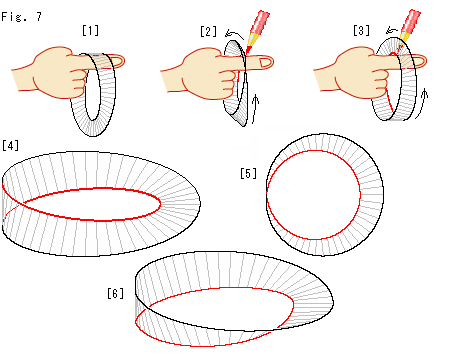 Fig.7をご覧ください。
Fig.7をご覧ください。
メビウスの帯の縁は1本だけで、内側の縁とか外側の縁といったものはありません。 しかし、ループとしては、内側と外側があります。 ループであることと縁とのかかわりを見てみましよう。 あまり柔らかくないメビウスの帯を使います。
[1]: 輪の中に指を通します。 ちゃんと通すことができます。
[2]: 通した指を動かさずに、メビウスの帯を回していきます。 そのとき、指が触れている縁に赤い色をつけていきます。 図のメビウスの帯は式(2)でつくったものですが、紙でつくったようなものでも同様にできます。
[3]: さらに回して、赤い色をつけていきます。
[4]: 色づけのおわったメビウスの帯です。 指がメビウスの帯の縁に触れていたところは、赤い線のところだけでした。 [1]のように指がメビウスの帯に触れるたときに、指とメビウスとの接点がジャンップしていたのです。
[5]: [4]を縮小して、上から見たものです。
[6]: [4]の左端を切り、こちら側の捻じれを戻して継ぎなおしたものです。 私たちの指は、この継ぎなおした赤いループの内側をなぞっていたのといってもよいでしよう。 しかし、実際は指の方が、メビウスの帯の捻じれをキャンセルするような動きをしていたのです。 図は歪んだループですが、全体としては捻じられていません。 黒い縁と赤い縁は、別々のループになっています。
 話しがややこしくなりました。 もう少し巧く見るために、メビウスの帯のフレームに石鹸膜を張ってみます。
話しがややこしくなりました。 もう少し巧く見るために、メビウスの帯のフレームに石鹸膜を張ってみます。
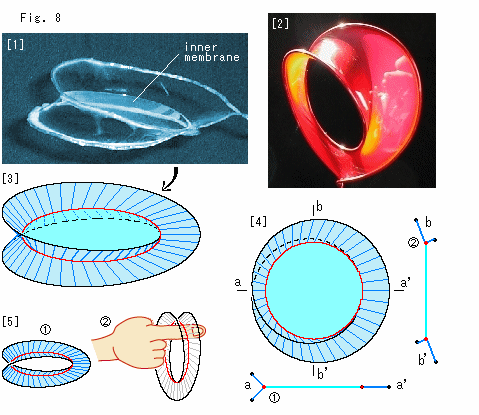
Fig.8をご覧ください。
[1]: 石鹸膜を張った写真です。 ちょっとわかりにくいですが、石鹸膜がY字形に交差して中央にも膜(membrane)が張られているのが見えます。
[2]: この写真では、中央が空洞で、上の方がU字形になっています。 Webの Membrane Structures からコピーしたものです。 美しいですね。 しかし、ここでは[1]のもので考えていきます。 膜の面が単純で見てとりやすいからです。
[3]: 写真[1]を図になおしたものです。 うす青色と水色のところが石鹸膜です。 赤い曲線は膜面が三叉になっているところの交線です。
[4]: [2]を真上から見たものです。 石鹸膜はこちら側から見える面だけを描いてあります。  はaa'の断面で、
はaa'の断面で、 はbb'の断面です。
はbb'の断面です。
[5]:  水色のところの石鹸膜を捨てると、面が">"形のメビウスの帯が得られます。 実際の石鹸膜で浮いている水色のところの膜を破ると、膜の張力で写真[2]のようになってしまいます。 それでもよいのですが、パソコンでは">"形の面のメビウスの帯を簡単に描けます。
水色のところの石鹸膜を捨てると、面が">"形のメビウスの帯が得られます。 実際の石鹸膜で浮いている水色のところの膜を破ると、膜の張力で写真[2]のようになってしまいます。 それでもよいのですが、パソコンでは">"形の面のメビウスの帯を簡単に描けます。
 それに指を通したものです。 指は、赤い1本の連続したループに触れているだけです。 いいかたを変えれば、メビウスの帯の面が">"形に折れているなら、その赤い稜線がメビウスの帯の内側の縁だといってもよいですね。 でも、これはメビウスの帯の縁ではありません。
それに指を通したものです。 指は、赤い1本の連続したループに触れているだけです。 いいかたを変えれば、メビウスの帯の面が">"形に折れているなら、その赤い稜線がメビウスの帯の内側の縁だといってもよいですね。 でも、これはメビウスの帯の縁ではありません。
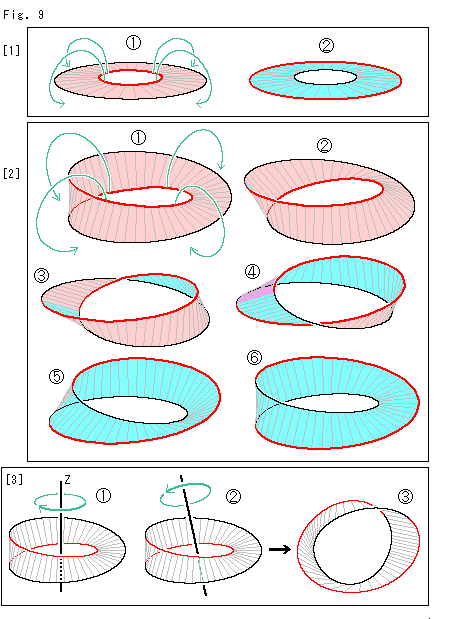
Fig.9をご覧ください。
輪の内側と外側は簡単に交換できます。 ふつうの輪とメビウスの帯では、どう違うでしようか。
最初に見えている面をピンク色に、見えていない面を水色に塗り分けておきます。 縁は、内側を赤色に外側を黒色にしておきます。 メビウスの帯では、Fig.7の[4]のように染めておきます。 そして、あまり硬くないものでします。
[1]: 穴のあいた円板です。
 緑色の矢印のように赤い内側のへりを外の方へ、黒い外側のヘリを中の方へひねります。
緑色の矢印のように赤い内側のへりを外の方へ、黒い外側のヘリを中の方へひねります。
 すると、180
すると、180 ひねったところで内側と外側が入れ替わった同じ形の円板が得られます。 円板は裏返っていますが、問題はありません。 このまま裏返せばよいのですから。
ひねったところで内側と外側が入れ替わった同じ形の円板が得られます。 円板は裏返っていますが、問題はありません。 このまま裏返せばよいのですから。
[2]: メビウスの帯です。
 矢印のように赤いへりを外へひねり、黒いへりを中へ押し込んでいきます。 このひねり方は[1]と同じですが、ひねるために捉えるところが違っています。
矢印のように赤いへりを外へひねり、黒いへりを中へ押し込んでいきます。 このひねり方は[1]と同じですが、ひねるために捉えるところが違っています。
 少しひねったところです。 左の方に、見えていなかった水色のところが覗けています。 続けてひねっていくと、順に
少しひねったところです。 左の方に、見えていなかった水色のところが覗けています。 続けてひねっていくと、順に ,
, ,
, ,
, のようになっていきます。
のようになっていきます。
 180
180 ひねったときです。 これは、
ひねったときです。 これは、 の赤と黒の縁を交換したものものになっていて、最初に見えなかった水色の面の全体がいま見えています。
の赤と黒の縁を交換したものものになっていて、最初に見えなかった水色の面の全体がいま見えています。
しかし、全体としてみると、メビウスの帯は面も縁も1つしかないのですから、 と
と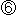 に差異はありません。 裏返っているともいえません。
に差異はありません。 裏返っているともいえません。
[3]: 面をひねらなくても、ただ向きを変えるだけで、[2]の過程のどの形にもなります。  のように回してもよいし、
のように回してもよいし、 のように適当なところに軸をとって回しても同じ姿のものが見られます。 メビウスの帯は回しているうちに、さまざまな姿態を見せます。
のように適当なところに軸をとって回しても同じ姿のものが見られます。 メビウスの帯は回しているうちに、さまざまな姿態を見せます。  は、その一つです。
は、その一つです。
式(1)で見てみましよう。 Z軸を中心にしてメビウスの帯を角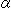 回すことは、
回すことは、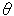 を変えて
を変えて
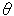
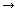
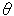 +
+ 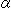
とすることです。 一方、角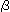 ひねることは、
ひねることは、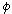 を変えて
を変えて
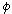
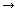
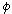 +
+ 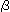
とすることです。 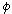 と
と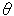 は、
は、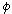 =
= 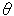 /2 でむすばれているのですから、いずれをいじくっても同じです。 Z軸の周りでなく、[3]の
/2 でむすばれているのですから、いずれをいじくっても同じです。 Z軸の周りでなく、[3]の のように回しても、 回すだけですから、とうぜん形は変わりません。 つまり、メビウスの帯はどんなにひねっても、回しても変わらないのです。
のように回しても、 回すだけですから、とうぜん形は変わりません。 つまり、メビウスの帯はどんなにひねっても、回しても変わらないのです。
このようになっているので、メビウスの帯と穴あき円板とはまったく性質が異なります。 しかし、円板においても、縁の内外と面の表裏を区別しなければ、メビウスの帯と同様に何の変化も生じないといえます。 また、見えている側を表とすると定めれば、メビウスの帯も裏返せることになるわけですね。
「表裏の区別ができない」ということと「表裏の区別をしない」ということは、まったく異なります。 意図的に表裏の区別をするにしても、何を表とし何を裏とするかによって変わってきます。 たとえば、テーブルの上に花瓶が一つあって、ほかにはなにも置かれていないとします。 そして、彼女が「あの綺麗な花瓶の裏側をご覧なさい」というのを聞いた彼は、花瓶のこちらからは見えない表面を見よといわれたと解しました。 これは、まったく自然なことですね。 そのときの二人の間には、花瓶の表裏が暗黙のうちに定義されていたのです。
メビウスの帯で表裏の区別ができないというのは、面をなぞっていってのことです。 メビウスの帯では面に印しをつけても役立ちません。 どこにどう印しを付けても、表裏を区別することができないのです。
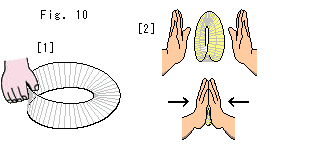 Fig.10をご覧ください。
Fig.10をご覧ください。
[1]: メビウスの帯は単側ですが、図のように手で持つことができます。 それは、部分的にはメビウスの帯にも表裏がある、つまり両側があるからです。
[2]: 小さな紙切れは、その両面全体を両手のひらに挟みこむことができます。 しかし、メビウスの帯は、それがどんなに小さくても、その面全体を両手のひらの間に挟むことはできません。 押しつぶすようにしても、手のひらに触れないところが残ります。
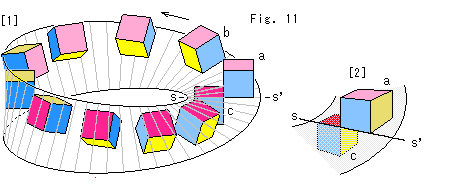 Fig.11をご覧ください。
Fig.11をご覧ください。
[1]: 立方体をメビウスの帯上で滑らせます。 立方体の対向面は濃淡の赤青黄で色分けしています。 立方体aはスタートラインss'に置かれているものです。 それを濃い赤色の面がメビウスの帯につねに接するようにして動かします。 立方体bが3つの淡い色の面を見せています。
[2]: スタートラインss'の様子をななめから見たものです。 一周してスタートラインss'にもどってきた立方体cは、立方体aと比べると、上下と左右の面が逆になっていて、sの方にずれた下側に移っています。
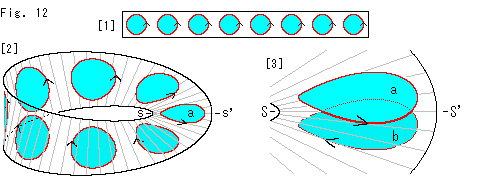 Fig.12をご覧ください。
Fig.12をご覧ください。
円ではどうなるでしようか。
[1]: 円を短冊上に並べたものです。 矢印は、赤い円周がいわゆる有向円であることを表しています。
[2]: 円が乗っている短冊を拡大してメビウスの帯にしたものです。 メビウスの帯の面が捻じれているので、円が歪んでいます。 円aはスタートラインss'にある円です。
[3]: 円bはメビウスの帯を1周してスタートラインss'にもどってきたものです。 はじめの円aと1周してきた円bをメビウスの帯の上下に浮かせて描いています。 円bは裏返って、赤い円周の向きが逆になっています。 円の内部の点も円周と同様に動きます。
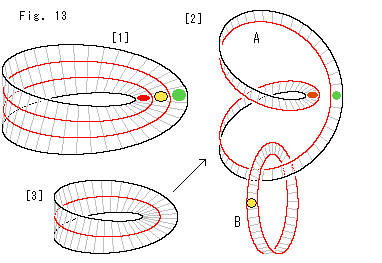 Fig.13をご覧ください。
Fig.13をご覧ください。
メビウスの帯を縁に沿った方向に切ってみます。
[1]: メビウスの帯に赤、黄、緑の印しを入れておいて、赤い線のように切ります。
[2]: 切ったものをほぐと2つの絡み合ったループAとBができます。 ループAは、Fig.5の[4]とは作り方はちがいますが、それと同じものになっています。 表裏のある面です。 そして、いま見えている赤い印しは、メビウスの帯[1]の反対側です。 ループBは、新しいメビウスの帯です。
[3]: メビウスの帯を1周するだけで切ります。 すると、[2]のループAだけが得られます。 このようにメビウスの帯は、そのループを切断しなくても、表裏のある面になります。
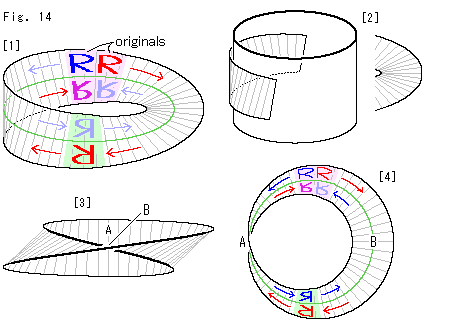 Fig.14をご覧ください。
Fig.14をご覧ください。
文字を動かして、詳しく見てみます。
[1]: 式(2)によって作図したメビウスの帯には、向かい合った面が縦横を含めてほぼ平行な面になっているところがあります。 そこをピンクと草色に染めています。 向こう側のピンク地のセンターラインの上側にある明るい赤と青の文字Rが、はじめに置いたもの(originals)です。 そこから、赤いRを赤い矢印のように右回りに、青いRを青い矢印のように左回りに動かします。 こちら側の草色のところへくると、赤いRは180 回転して、上下と左右が逆になり、センターラインの下側にきています。 青いRは左右を逆にして裏返っています。
回転して、上下と左右が逆になり、センターラインの下側にきています。 青いRは左右を逆にして裏返っています。
続けて動かし、1周してもとのピンクのところに戻すと、赤と青のRはともにセンターラインの下側にきます。 そして、こんどは赤いRが左右を逆にして裏返り、青いRが裏返ったままで180 回転して上下を逆にしています。 赤と青のRはともに裏返って逆立ちしています。 この動きの間、2つの文字Rは終始その足元をセンターラインに沿わせています。
回転して上下を逆にしています。 赤と青のRはともに裏返って逆立ちしています。 この動きの間、2つの文字Rは終始その足元をセンターラインに沿わせています。
文字Rの動きは、右回りと左回りで変化の様子が異なっているように見えますね。 それは、メビウスの帯の右半分(半周)で180 の捻じれをしてしまっていると見える方向に描かれているからです。
の捻じれをしてしまっていると見える方向に描かれているからです。
[2]: 円筒の絵にメビウスの帯の左の方を当ててみると、あたかも円筒の一部に巻きついているように見えます。 メビウスの帯の右の方は、捻じられているとはいえないくらいの歪みしかない同心円の一部のように見えます。 メビウスの帯も、その上の図形も式(2)によって描いたものですから、全周にわたって公平にねじられています。 それなのに、どうしてでしようか?
[3]: 右から真横に[1]のメビウスの帯を見たものです。 こちら側のB ([1]の右側) で、180 捻じれてしまっているようです。 しかしキザミ線をよく見ると、向こう側A ([1]の左側) から捻じりはじめて、こちら側のBで捻じれが完結しています。
捻じれてしまっているようです。 しかしキザミ線をよく見ると、向こう側A ([1]の左側) から捻じりはじめて、こちら側のBで捻じれが完結しています。
[4]: 真上から[1]のメビウスの帯を見て、小さく描いたものです。 これだと、比較的公平に全体が見れます。 こんどは、左の方のAのところで捻じられているように見えます。 いや、そこは面が画面に垂直になっているので、視線でメビウスの帯を1周してわかるように、局所のAで捻じれているのではありません。 ぐるっと全体を廻って捻じれているのです。
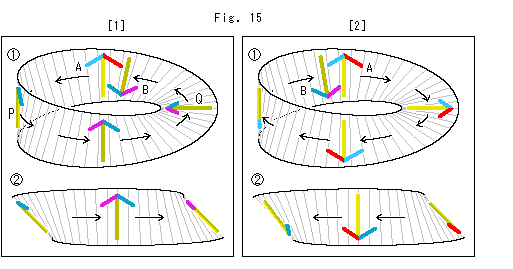 Fig.15をご覧ください。
Fig.15をご覧ください。
文字でなく、矢型を動かしてみます。 上と同じことですが、右回りと左回りのちがいを調べます。
[1]:  のAは始めの矢型で、Bは1周して戻ってきた矢型です。 1周すると、向きを逆にして裏返ります。 途中の矢型Qは矢型Pから90
のAは始めの矢型で、Bは1周して戻ってきた矢型です。 1周すると、向きを逆にして裏返ります。 途中の矢型Qは矢型Pから90 (半周分)捻じれています。
(半周分)捻じれています。  は左から真横に
は左から真横に を見たものです。 この図でも左から右へいく間に90
を見たものです。 この図でも左から右へいく間に90 (半周分)捻じれているはずです。 頭の中で視線を黒い矢印の方向にとり、メビウスの帯の面に沿って矢型を追っていけば、捻じれていく具合がわかります。 しかし、そうするにしても、つかみにくいですね。 どこでも公平に捻じられているとわかっているのに。
(半周分)捻じれているはずです。 頭の中で視線を黒い矢印の方向にとり、メビウスの帯の面に沿って矢型を追っていけば、捻じれていく具合がわかります。 しかし、そうするにしても、つかみにくいですね。 どこでも公平に捻じられているとわかっているのに。
[2]: 逆方向に動かしてみたものです。 やはり、この画面を見ているだけでは、公平に捻じられて行く様子をくみ取りにくいですね。 慣れれば、そうではないのですが。
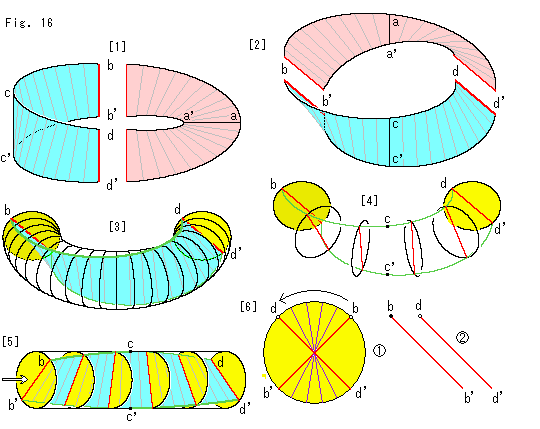 Fig.16をご覧ください。
Fig.16をご覧ください。
頭の中で視線を変えることをトーラスをつかって調べてみましよう。
[1]: メビウスの帯を2分して、わかりやすいように染め分けしておきます。 各部に記号は、どこがどうなっているかを見るためのものです。まず、水色のとろに注目します。
[2]: 水色のところがこちら側へくるように[1]を回したところです。
[3]: 2分したソリッドトーラスの中に水色のところが入っているとして描いたものです。 そして、このトーラスは円板を連ねたものであると考えます。 円板は表裏があるので、それを黄色い濃淡で表現しています。 明るい黄色が表で、暗い黄色が裏だとしておきます。
[4]: ソリッドトーラスからメビウスの帯の縁といくつかの円板だけを取り出したものです。
[5]: これを真直ぐなシリンダーにします。 こうすれば、ねじれ具合がよくわかります。 どの円板も、表側が見えています。 白い矢印は、透して視ようとする方向です。
[6]: シリンダーを透して視た様子を拡大して描いたものです。
 点bb'から点dd'まで行く間に90
点bb'から点dd'まで行く間に90 回転しています。 点bと点dを小さな丸で描いてあるのは、それらを円板の表側で見ていることを表しています。
回転しています。 点bと点dを小さな丸で描いてあるのは、それらを円板の表側で見ていることを表しています。
 シリンダーが真直ぐではなくて、もとのU字形(トーラスの半分)だとすると、線分bb'が乗っている円板は、こちらから見て裏側になります。 図は、そのように線分bb'を回したところです。 いま線分bb'は円板の裏側から視ているので、点bを黒いスポットで描いてあります。 そして、2つの線分bb'と線分dd'は平行になっていて、点bと点dがともに上側にあります。
シリンダーが真直ぐではなくて、もとのU字形(トーラスの半分)だとすると、線分bb'が乗っている円板は、こちらから見て裏側になります。 図は、そのように線分bb'を回したところです。 いま線分bb'は円板の裏側から視ているので、点bを黒いスポットで描いてあります。 そして、2つの線分bb'と線分dd'は平行になっていて、点bと点dがともに上側にあります。
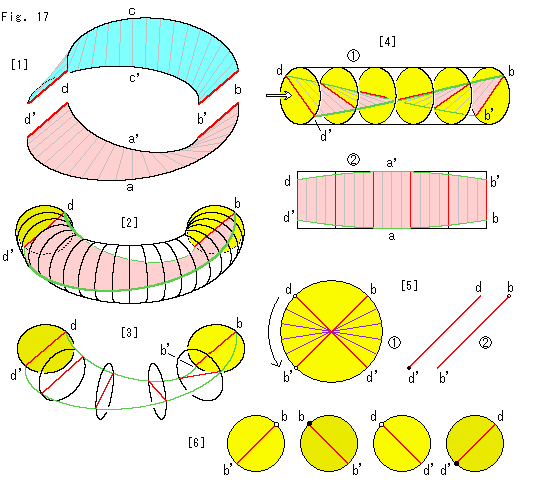
Fig.17をご覧ください。
こんどは2分したメビウスの帯のピンク色の方を見てみます。 上と同じ要領ですが、異なるところが見出されます。
[1]: ピンク色の方をこちらへ向けます。
[2]: ソリッドトーラスの中です。 やはり、左に円板の裏側が見え、右に円板の表側が見えます。
[3]: メビウスの帯の縁といくつかの円板です。
[4]: シリンダーにしたところです。
 db'とd'bが直線状に見えています。
db'とd'bが直線状に見えています。
 シリンダー
シリンダー を真上から見たものです。 a,a'のところで一番巾広く見えます。
を真上から見たものです。 a,a'のところで一番巾広く見えます。
[5]: [4]のシリンダー を軸方向に見たものです。
を軸方向に見たものです。
 やはり90
やはり90 回転しています。 しかしこんどの動き方はFig.16の場合と90
回転しています。 しかしこんどの動き方はFig.16の場合と90 ずれています。 180
ずれています。 180 のずれではありません。
のずれではありません。
 シリンダーをもとのU字形にしたときの線分bb'とdd'です。 この場合も、2つの線分bb'と線分dd'は平行になっています。 しかし、点bは上側で点d'は下側です。 これがFig.16と異なるキーポイントです。 そのために、文字Rや矢型の動きが妙に見えたのです。
シリンダーをもとのU字形にしたときの線分bb'とdd'です。 この場合も、2つの線分bb'と線分dd'は平行になっています。 しかし、点bは上側で点d'は下側です。 これがFig.16と異なるキーポイントです。 そのために、文字Rや矢型の動きが妙に見えたのです。
[6]: そうはいっても、Fig.16の平行線分 bb'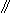 dd' とこのFig.17の平行線分 dd'
dd' とこのFig.17の平行線分 dd'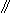 bb' は継ながるのでしようか。 続いていたものを切ったのですから、まちがいなく継ながるはずです。 念のために、それらの線分を円板の表裏に乗せて並べてみました。 ちゃんと継ながります。
bb' は継ながるのでしようか。 続いていたものを切ったのですから、まちがいなく継ながるはずです。 念のために、それらの線分を円板の表裏に乗せて並べてみました。 ちゃんと継ながります。
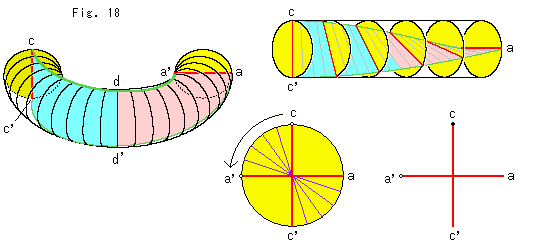
Fig.18をご覧ください。
ついでに、水色とピンク色のところがつづいている状況を描いておきます。 左の方から見ると、急旋回した飛行機が安定飛行にもどるときの翼の動きに似ています。
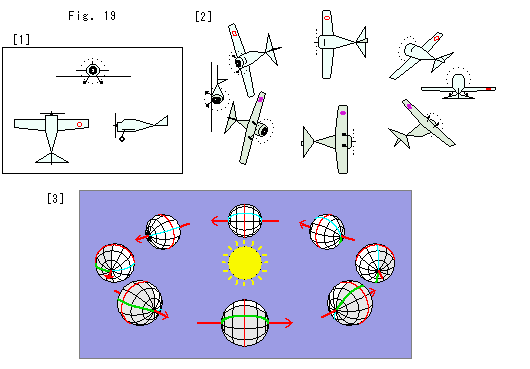 Fig.19をご覧ください。
Fig.19をご覧ください。
[1]: メビウスの帯の面の具合は、飛行機のアクロバット飛行を想うと、つかみやすいです。 この三面図のプロペラ飛行機を飛ばします。
[2]; 飛行機は寝返りながら旋回します。 1周すると、正確に寝返ります。 この飛行機は、きっちり偶数回旋回しなければなりません。 そうしないと、着陸できないからです。
[3]: 惑星の運動です。 中央の黄色いのが太陽です。 こんなものを想うのもまよいでしよう。 この惑星の公転軌道は、メビウスの帯のセンターラインです。 赤い矢線で描かれている自転軸は公転軌道の接線方向になっています。 そのため、四季はありません。 天空に固定した北極星に相当する星もありません。 そして、1年は半日で、2年して1日がおわります。 図は、その1年(1周)分です。 この惑星の住人はメビウスの帯を毎日2周しているのです。 24時間で2年! 惑星上の赤い曲線は赤道です。 水色の曲線は日付変更線にとったところで、その反対側の曲線を本初子午線としてこい緑色にしています。
こうして見てきたことは、いずれもいうまでもないことです。 けれども、はじめにメビウスの帯の絵を見たときに、わかった気持ちになったのが如何におぼつかないものであったかを知ることができました。
ところで、ものの前後左右上下を同時に見ることは、テレビカメラなどをつかえばできます。 しかし、見慣れたものでないかぎり、すぐに正しく認識できるでしようか。
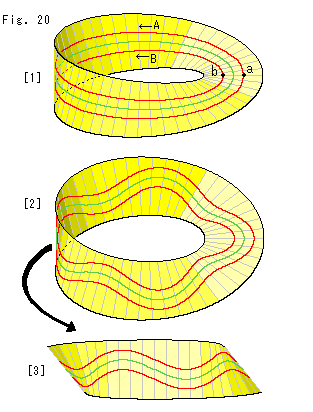
Fig.20をご覧ください。
メビウスの帯の上に線を引いてみます。
[1]: 緑色の線はセンターラインです。 点aから左回りに赤い線が伸びて行くとします。 それは、1周するとセンターラインの反対側の点bへきます。 もう1周すると、もとの位置aにもどります。 この間、赤い線は中央線をけっして横切りません。 それなのに、センターラインの両側を赤い線は走っています。 図の赤い線は、部分的に見ると平行線のようにも見えますが、そうではありません。 Aの道とBの道は1本に連なっています。
緑色のセンターラインは、道路の中央分離帯とはちがって、メビウスの帯を二分するものではありません。 この線に沿って切ってもメビウスの帯は分離できません。 ループの長さが2倍になるだけです。 メビウスの帯の上には、対向車線はないのです。 交通規制するにも、一方通行しかできません。
[2]: センターラインをジグザグにしてみました。 こうしても、[1]と同じ結果になりす。
[3]: [2]の左側が見えくいので、こちら側へ向けてみたものです。 赤と緑の線は、たしかに交わっていません。
 無限遠を含めたときのメビウスの帯の上での様子を見ようとするのですが、その前に有限の範囲で直線がどうなるのかを見ておきます。 直接メビウスの帯の上に描くのではなく、短冊に線を引いておいて、それをメビウスの帯にします。
無限遠を含めたときのメビウスの帯の上での様子を見ようとするのですが、その前に有限の範囲で直線がどうなるのかを見ておきます。 直接メビウスの帯の上に描くのではなく、短冊に線を引いておいて、それをメビウスの帯にします。
Fig.21をご覧ください。
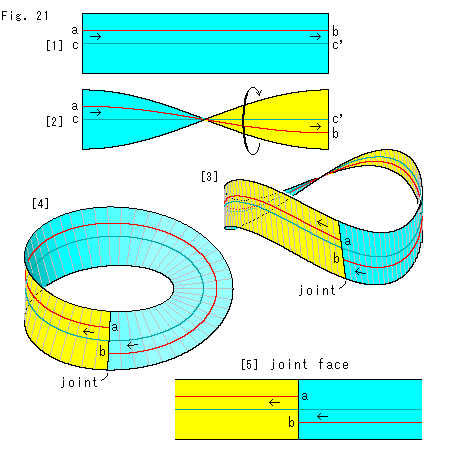
[1]: 紙を短冊に切って、緑色のセンターラインから等距離のところに赤い線abを引きました。 赤い線abは、短冊の長さに限りがあるので、直線ではなく線分です。 図の短冊の長さは、実際の1/2より小さく描いてあります。 そうすると、短冊としてのねじった効果が顕著に見えるからです。 矢印は観察の便のために、線分に向きをつけたものです。
[2]: 短冊を180 ねじります。 黄色いところは裏側です。
ねじります。 黄色いところは裏側です。
[3]: ねじた短冊の両端をこちらの方へ公平に曲げて継なぐと、メビウスの帯になります。 メビウスの帯になれば表裏はなくなるのですが、短冊のときに裏側であったところの色をわざとそのままにして描いてあります。 どこがどうなったのかを判然とさせるためです。 継ぎ目(joint)はこちら側にきますが、向こう側が見にくいですね。 紙やゴム板の短冊では、どうしてもこうなります。
[4]: 式(2)を使って描きなおしたものです。 式(2)には、この継ぎ目に関する制約はありません。 好みの大きさの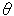 のところを継ぎ目にすればよいのです。
のところを継ぎ目にすればよいのです。
赤い線は、センターラインでないかぎり、継ぎ目のところでは継ながりません。 この赤い線を同じ調子で伸ばしていけば、もう一周してbのところに戻って継ながるわけですが、その分は短冊にはありません。
[5]: メビウスの帯を継ぎ目と反対側で切って、あらためて短冊に広げたものです。 この継ぎめ面(joint face)を[1],[2]とよく見比べてください。
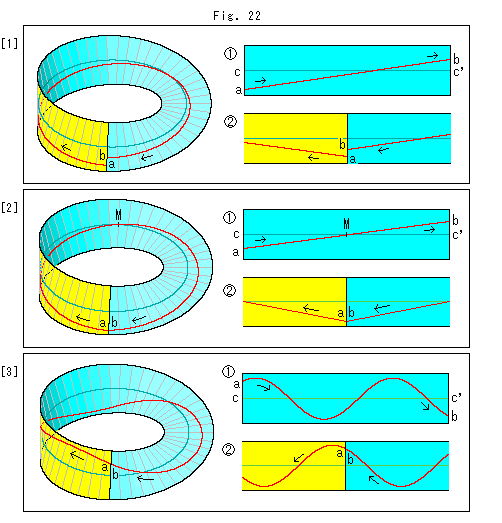
Fig.22をご覧ください。
もとの短冊上の線がメビウスの帯上でどうなるかを継ぎめ面の短冊で見ていきます。 上と同じ要領で、短冊の長さを短く描きます。
[1]: 真直ぐな赤い線abを斜めにして緑色のセンターラインを横切らせました。  はもとの短冊で、
はもとの短冊で、 は継ぎめ面の短冊です。 継ぎめのところでは、やはり点a,bは離れたままです。
は継ぎめ面の短冊です。 継ぎめのところでは、やはり点a,bは離れたままです。
[2]: 特別な場合です。 直線abが短冊 のちょうど真ん中Mでセンターラインを横切っています。 こうすると、距離acと距離bc'は等しくなり、
のちょうど真ん中Mでセンターラインを横切っています。 こうすると、距離acと距離bc'は等しくなり、 のように継ぎめで赤い線がつながります。 しかし、V字形に継がっていて滑らかではありません。 メビウスの帯上でも、しかとは見えませんが、そうなっています。
のように継ぎめで赤い線がつながります。 しかし、V字形に継がっていて滑らかではありません。 メビウスの帯上でも、しかとは見えませんが、そうなっています。
[3]: サインカーブです。 短冊 では、ちゃんとしたサインカーブですが、そのことをメビウスの帯の上から見て取ることは、すぐにはできませんね。 サインカーブはcc'を3
では、ちゃんとしたサインカーブですが、そのことをメビウスの帯の上から見て取ることは、すぐにはできませんね。 サインカーブはcc'を3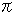 (
(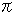 の奇数倍) の長さにとって描いています。 こうすると、継ぎめでなめらかに継がります。
の奇数倍) の長さにとって描いています。 こうすると、継ぎめでなめらかに継がります。
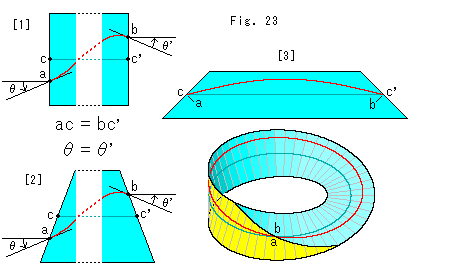 Fig.23をご覧ください。
Fig.23をご覧ください。
[1]: 上でつかめたことです。 それは、メビウスの帯の継ぎ目で曲線がなめらかに継がるのは、もとの短冊の両端において図のようになっている場合でした。
[2]: 短冊が長方形でなくても、台形なら、同じ条件で曲線をなめらかに継ぐことができます。 (平行四辺形の短冊では、曲線も帯の縁もなめらかにはなりません。)
[3]: 台形の短冊をメビウスの帯にしたものです。 両端をセンターラインの端と一致させたサインカーブ(0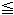
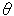
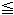
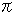 )です。 上の条件は満たされているので、メビウスの帯上の赤い線はなめらかに継がっています。
)です。 上の条件は満たされているので、メビウスの帯上の赤い線はなめらかに継がっています。
それでは、メビウスの帯の上での無限の彼方の様子を、次の章へ移って見ていきましよう。
[前章] [次章] [目次]


 Fig.3をご覧ください。
Fig.3をご覧ください。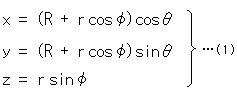
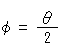
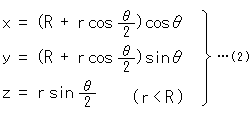

 Fig.5をご覧ください。
Fig.5をご覧ください。 Fig.6をご覧ください。
Fig.6をご覧ください。 Fig.7をご覧ください。
Fig.7をご覧ください。 話しがややこしくなりました。 もう少し巧く見るために、メビウスの帯のフレームに石鹸膜を張ってみます。
話しがややこしくなりました。 もう少し巧く見るために、メビウスの帯のフレームに石鹸膜を張ってみます。
 ,
, Fig.10をご覧ください。
Fig.10をご覧ください。 Fig.11をご覧ください。
Fig.11をご覧ください。 Fig.12をご覧ください。
Fig.12をご覧ください。 Fig.13をご覧ください。
Fig.13をご覧ください。 Fig.14をご覧ください。
Fig.14をご覧ください。 Fig.15をご覧ください。
Fig.15をご覧ください。 Fig.16をご覧ください。
Fig.16をご覧ください。

 Fig.19をご覧ください。
Fig.19をご覧ください。
 無限遠を含めたときのメビウスの帯の上での様子を見ようとするのですが、その前に有限の範囲で直線がどうなるのかを見ておきます。 直接メビウスの帯の上に描くのではなく、短冊に線を引いておいて、それをメビウスの帯にします。
無限遠を含めたときのメビウスの帯の上での様子を見ようとするのですが、その前に有限の範囲で直線がどうなるのかを見ておきます。 直接メビウスの帯の上に描くのではなく、短冊に線を引いておいて、それをメビウスの帯にします。
 Fig.23をご覧ください。
Fig.23をご覧ください。