第３部 射影幾何から双曲幾何へ
Ch.38 メビウスの帯 (2) 
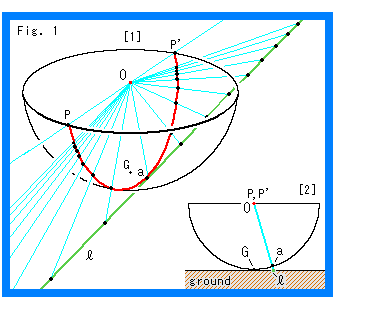
メビウスの帯の上での無限の彼方の様子を見るために、Ch.31でも使った半球を利用します。
Fig.1をご覧ください。
[1]: 赤いスポットは半球Oの中心です。 点G(南極)は、半球面と平面との接点です。 緑色の線
は、半球Oを置いた平面上(地上, ground)の直線です。 半球Oの縁(赤道)は無限遠直線(line at infinity)で、水色の線は、直線を半球面へ移す射線です。 赤い曲線PP'が、その移されたもので、半球の大円になっています。 点aは、赤い曲線PP'の中点です。 この赤い曲線は無限の彼方まで伸びている直線とみなせるものですから、それをメビウスの帯に乗せるとどうなるかを見ようとしています。
[2]: [1]の3点O,a,Gの位置関係をはっきりさせるために、その3点を通る平面で半球を切った断面です。 大円PP'とその中点aは、つねにこのような関係になっています。 いま点aは点Gをから少し離れたところにあって、直線とは接していませんが、点aと点Gが重なる場合もむろんあります。
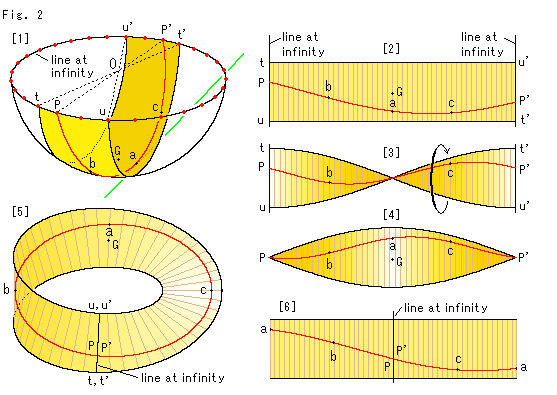Fig.2をご覧ください。
[1]: 半球面Oの縁(無限遠直線)に並んでいる赤いスポットは無数にある対心点を表しています。 点線は、赤い曲線(=直線)PP'とそれを挟んでいる点t,t'、点u,u'が対心点になっていることを表現しています。 半球面を図のように切ります。 赤い曲線PP'が2曲線tt'とuu'の間にあれば、どのような切り方でもかまいません。 しかし、赤道面に垂直に切ると作図しやすいので、図ではそのようにしています。 点a,b,cと点Gは、半球面O上の点がメビウスの帯のどこに移るかを追うための目印しです。
[2]: 半球面Oを切り出して短冊にしたものです。 半球面をゴムのように扱い、平たくしています。 短冊の上では直線になっていません。 この短冊は両端が無限遠直線ですので、その長さを無限大だと想ってもかまいません。 ただし、その無限大は私たちの手もとに引き寄せたものです！
[3]: [2]の左端を固定して、右端を180
捻ったところです。
[4]: [3]を上から見たものです。
[5]: [2]の両端を継ないで、メビウスの帯にしたところです。 無限遠直線の反対側が点aのところにです。 こんどは、赤い線がなめらかに続いています。 これが射影平面の性質です。
[6]: [5]を点aで切って、あらためて短冊に広げてみたものです。
このように、無限の彼方へと伸びている直線の両端が、その彼方で結ばれていることをつかみ出せたというわけです。 そして、赤い"直線"は歪んだ面であるメビウスの帯上にあるのですが、直線としての性質は失われていません。
実際の無限の彼方で直線がこのようになっているかどうかは、誰にもわかりません。 しかし、こうだとすることに不合理を感じることもありません。 むろん、無限の彼方というものが存在するとして、また、直線はその無限の彼方まで伸ばせると公理化(仮定)しての話しです。
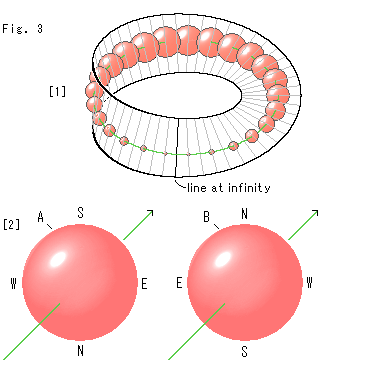
Fig.3をご覧ください。
無限遠直線を横切るものが大きさのある物体の場合は、どうなるでしようか。
[1]: スケルトンのメビウスの帯に緑色の直線を引きます。 それに同じ大きさの半透明の球を数珠のように通してみました。 球と球との中心間隔は視覚的な等間隔にとって絵描いてありますが、自由に動かせます。 無限遠直線に近づくほど球は小さく描かれ、無限遠直線上では大きさがありません。 大きさはなくても、存在しています。 無限遠直線を通り過ぎると、球は再び大きくなり、スタートポイントにもどると、もとの大きさになります。 無限遠直線を設けたメビウスの帯の上では、ものの大きさが(見た目に)このようになってしまうのです。 スタートポイントをどこにとっても変わりありません。
[2]: スタートポイントでじっとしていた球Aと、無限遠直線を横切り1周してもどってきた球Bです。 2つの球の矢印の向きに変わりはありませんが、球Bは球Aとくらべると、北極Nと南極Sが逆転しており、東Eと西Wも入れ替わっています。 無限遠直線を横切ってもどってきたものは、どんなものもこのようになるのです。 もちろん、もう1周すれば元にもどります。 有限でのこれまでの図とくらべ、ずいぶん様子がちがいます。
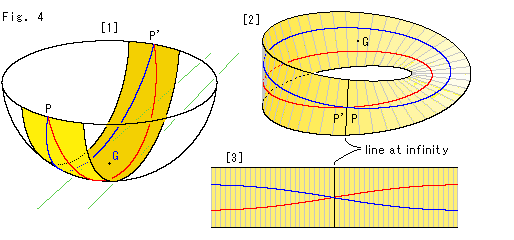Fig.4をご覧ください。
こんどは平行線です。
[1]: 半球面をメビウスの帯に切ります。 赤と青の線が平行線です。 簡単のために、平行線の真ん中に点G(南極)をはさんでいます。
[2]: 半球面の縁で向かい合っていた対心点P,P'が、いまメビウスの帯の無限遠直線上の1点になっています。 そして、平行線が完全なループになっているというわけです。
[3]: メビウスの帯を切って広げるとこうなるのですが、左右を無限の彼方で上下が逆につながっていると想像することで、意味のあるものになります。
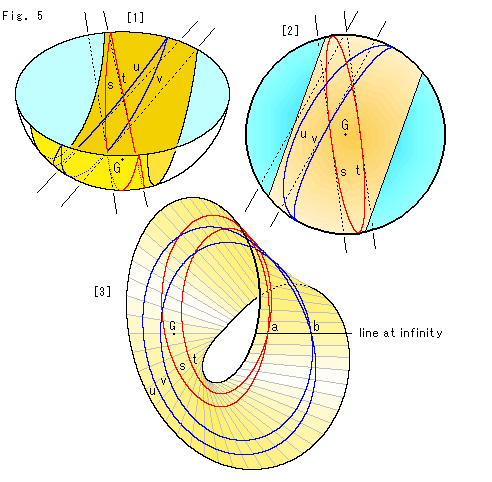
Fig.5をご覧ください。
2組の平行線の様子です。
[1]: 赤い2曲線s,t と青い2曲線u,v は平行線です。 赤い平行線s,tは点Gをはさんでますが、青い平行線u,vは逸れています。 1つのメビウスの帯に2組の平行線が乗るように半球をカットするので、その巾はかなり大きくなります。
[2]: [1]を真上から見たものです。
[3]: メビウスの帯です。 2組の平行線が交わっているところと無限遠直線の両方がよく見える向きに描いてあります。 2組の平行線は、それぞれが無限遠直線上で交わっています。 しかし、その2つの交点a,bの間の距離は、目には見えていますが無限大です。 ですから、このメビウスの帯は長さだけでなく、幅も無限大だと思っておかねばなりません。 無限遠直線上には、ふつうの距離というものがないのです。
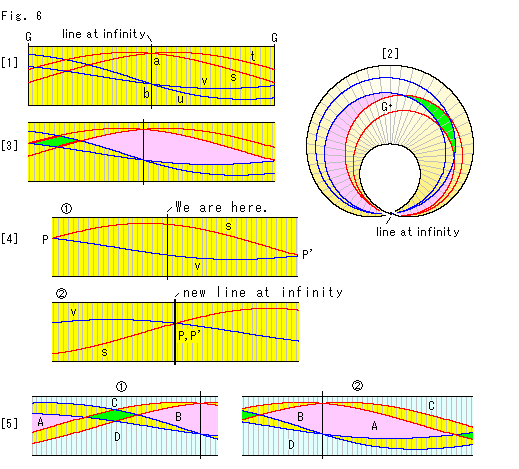Fig.6をご覧ください。
[1]: Fig.5のメビウスの帯を小さくして切り、短冊にしたものです。 真ん中の黒い縦線が無限遠直線で、左右の端が半球の底の点Gを通るキザミ線になっています。
[2]: Fig.5ではメビウスの帯は右上のあたりがよく見えないので、付近の状況がわかった無限遠直線を画面に垂直にして描きなおしたものです。 緑色とピンク色で染めてあるように、2つの四辺形ができています。 でも、ピンク色のところが四辺形であることは、すぐには見て取りにくいですね。
[3]: 短冊上でどちらの四辺形も分断されないように無限遠直線をすこしずらせて描いたものです。 どんな2組の平行線でも、このようにできます。 ふつうの平面上で2組の平行線が交わると、1つの平行四辺形ができます。 メビウスの帯の上では、緑色の平行四辺形のほかにピンク色の四辺形ができるのです。 ピンク色の四辺形は無限大の大きさで、無限遠直線にまたがっています。
[4]: 見方を変えてみます。
ひとまず、私たちは「無限の彼方で交わる2直線は平行である」ということに同意します。 そのうえで、赤い直線sと青い直線vに注目します。 
の短冊は[3]と同じもので、2直線s,vが両端でちょうど交わっています。 むろん平行線ではありません。 しかし、ここで文字通り立場を交換してみると、奇妙なことが起こります。 無限遠直線のあるところを、私たちがいるふつうの有限なところだとします。 すると、同一視される点P,P'のところが無限の彼方だということになります。 短冊の両端P,P'のあるところが新しい無限直線です。 2本の直線s,vは、この新しい無限の彼方で交わっています。 ですから、その2直線s,vは平行線であるということになります。 
は、そうなったとして、新しい無限直線を中央にもってきたものです。
はて、これはリクツにかなっているでしようか？ 平行線でなかったものが平行線になるなんて！ でも、これは正しいのです。 それが、無限遠直線というものの性質です。 と、いわれても、何かヘンですね。 おいおい考えていきましよう。
[5]: とは、[3]から色を塗った四辺形とそのぐるりを取り出したものです。 水色に染め替えたCとDのところも、メビウスの帯にしたときに継ながって、ひと続きになります。 もし短冊の巾(図の上下)を無限に大きくとることができれば、その方向の無限の彼方でもひと続きになっているはずですね。 無限に大きな巾の短冊がないなら、半球面の切り方を変えて、メビウスの帯を別にもう一つ作れば、C,Dのつながりの全域を見れます。 しかし、わざわざそうしなくても、CとDが短冊を横切る方向にもひと続きであることは容易に察しられますね。 ただし、短冊は長さだけでなく、幅も無限大だと想像しなければなりません。
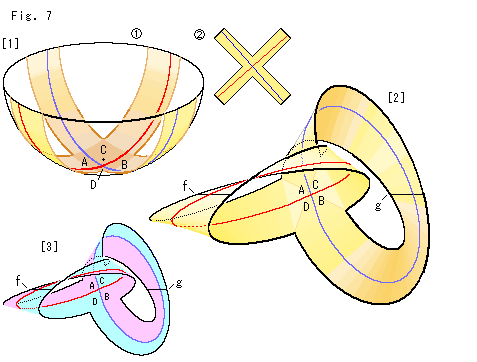
Fig.7をご覧ください。
メビウスの帯の形を変えてみます。 上ではA,Bの関係とC,Dの関係を同時に見ることができませんでしたが、A,B,C,Dの領域を公平に見れるようにします。 見やすくするために、2組の平行線のかわりに2本の直線で代用ます。 Fig.6の[5]の緑色の平行四辺形は、この2直線の交点に埋没させます。
[1]: 枝分かれしている赤と青の曲線がちょうど入るように、半球面をX字形に切ります。 は切り出したものです。 このX形の短冊の先端は、半球面の縁なので無限遠直線です。
[2]: X形短冊の先端をひねって図のようにつなぎます。 2つの短冊で作ったメビウスの帯を背中合わせにくっつけたものと同じです。 帯を横切っている黒い線f,gは継ぎ目の無限遠直線です。 無限遠直線が分断されているのが、ちょっと不都合ですね。
[3]: Fig.6の[5]にあわせて色をつけたものです。 AとB、CとDは、いずれも無限遠直線でつながっています。 AからBへは、fとgのどちらの無限遠直線を横切っても行くことができます。 しかし、AからCやDへ行くことは、赤か青の直線を横切らないかぎりできません。 C,Dについても同じ具合です。 A,B,C,Dを公平に見ても、状況はFig.6の[5]と変わらないことがわかりました。
**************************************************
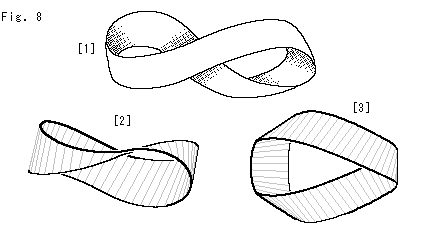
メビウスの帯が、紙などでつくったものと数式で描いたものとで、どうちがうのかを見てみます。
Fig.8をご覧ください。
[1]: 紙のメビウスの帯です。 ねじれている様子はよくわかりますが、帯の上で何がどうなっていくのかを見てとるには不向きです。 まず、座標軸を定めにくいですね。 しかし、見にくいのは、それだけではありません。
[2]: 向きを変えてみると、捻じれているところがよく見えます。 描き込んだ灰色の等間隔のキザミ線はどこも縁にほぼ垂直です。
[3]: さらに向きを変えてみました。 こうして見ると、3回捻じられていているのがわかります。 2回が同じ向きの裏返しで、1回が逆向きになっていて、差し引き1回だけの裏返しです。 このように余分な捻じれがあって、隠れたところが多いために、紙などでつくったメビウスの帯は見にくいのです。
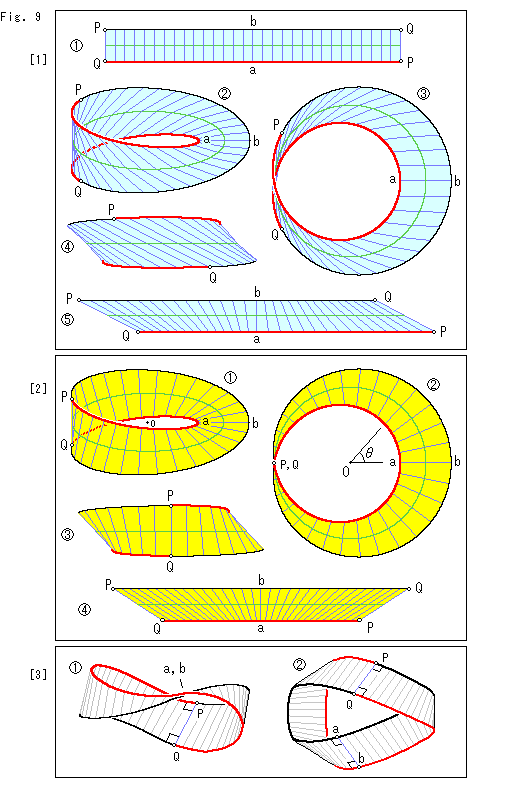Fig.9をご覧ください。
数式で描いたメビウスの帯と短冊との関係を見てみます。
[1]: 短冊の縁の長さが、そのままメビウスの帯の縁にになっているとした場合です。
短冊にn等分したキザミ線を入れて、緑色のセンターラインを引いておきます。 点P,Qは、ねじてメビウスの帯したときに継ながるところですので、目立つように丸印し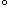 
をつけています。 短冊の片側を赤く塗ってあるのは、どちらの側がどうなるかを見るためです。
キザミ線がセンターラインのところで、すこし折れ線になっています。 精確に描けば緩くカーブしたものになりますが、目立たせるためにわざと省略しています。 図は、に比べ、拡大してあります。
真上から見たところです。
点P,Qの付近を左の方から見たものです。 キザミ線が、紙でつくったものとは違って、縁に垂直ではなく斜めにずれています。 キザミ線が縁と垂直になっているのは、点a,bのところだけです。
メビウスの帯と短冊は、縁とセンターラインの上の点だけが対応していて、ab以外のキザミ線の長さは一致していません。 そこで、短冊の縁をずらせてみたのが、この図です。 この平行四辺形とメビウスの帯のキザミ線は、長さも傾きも一致ているとしてよいでしよう。 しかし、紙をこのような平行四辺形に切ってメビウスの帯をつくると、継ぎ目のところが尖ってしまって、縁のなめらかなものにはなりません。
[2]: こんどは、先に式(2)でメビウスの帯を描いて、それを短冊に開く場合です。
緑色のセンターラインは円です。 その中心が点Oです。 センターラインを[1]と同様にn等分します。 その各点で、センターラインと直交する直線をキザミ線にしています。 キザミ線が粗く見えますが、本数は[1]と同じです。
真上から見たところです。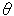 
がキザミ線の角です。 Fig.3を参照してください。 [1]では赤い縁と黒い縁の長さは等しくて、短冊のそれと同じでした。 この[2]では、そうではありません。 図の場合、黒い縁の長さは赤い縁の長さの1.5倍になっています。
点P,Qの付近を左横から見たものです。 キザミ線が、この点P,Qと点a,bの2か所で縁と垂直になっています。
メビウスの帯を、その縁の長さを保ながら開いたものです。 台形になっていて、キザミ線の長さも角も歪んでいます。 (図は縮小しています。)
[3]: 上でも描いた紙の短冊からつくったメビウスの帯です。 その縁を短冊の縁にあわせて赤と黒に染めています。 キザミ線の数は、見映えのために[1],[2]より多くしています。
当然ですが、赤と黒の縁の長さが同じであることが見てとれます。 そして、どのキザミ線も、同じ長さで縁とほぼ直角です。
点a,bと点P,Qの付近がともに見える向きでは、それらのところでの様子がまったく同じであることがわかります。
メビウスの帯と短冊は、どんな格好のものでも、両者の上の点は1対1で対応づけられます。 しかし、点の粗密といったようなものは、けっして一致しません。 紙で作ったメビウスの帯にもわずかな伸縮があります。 ただ、目立たないだけです。
上の[2]のメビウスの帯の赤い縁 P-a-Q を小回りのふち、黒い縁 P-b-Q を大回りの縁とよぶことにします。 すると、紙でつくったメビウスの帯の縁は、色分けされていますが、大回り小回りの区別はありません。 これが均整のとれた美しさの素です。
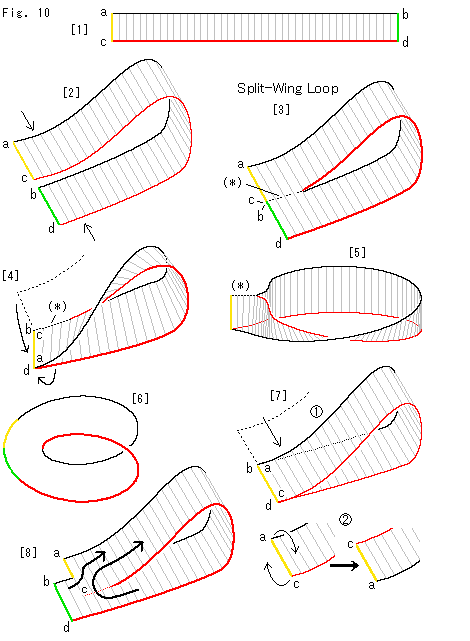Fig.10をご覧ください。
[1]: 短冊の辺を図のように色分けしておきます。
[2]: 短冊の一端を曲げて、両端をそろえ、そのあたりを平くします。 そして、矢印のように押して隅のbとcをくっつけます。
[3]: すると、裂け目をもったループができます。 点線(*)はつながっているところです。 こループは、数学の本には出てきませんが、スプリットウィング ループ(Split-Wing Loop)とよばれてるいものです。 スプリットウィングというのは鳥の翼の先端が裂けているところです。
どこも捻じれていないように見えていますが、面を辿っていってみると、表裏がありません。 本当は捻じれているのでしようか。
[4]: 矢印のように曲げて、黄色い辺acと緑色の辺bdを矢印のように合わせて継なぎます。 こんどは、捻じれているのがはっきり見えます。 スプリットウィング ループが捻じれたものだとすると、いま2回(360)ねじられていることになります。 おかしいですね。
[5]: [4]の巾をちぢめて穴に丸みをつけ、こちら側に倒してみたものです。 やはり、一度しかねじられていません。 つながっている(*)のところを離して、折れめを広げると、ふつうのメビウスの帯になります。
[6]: メビウスの帯の縁だけをとって、[3]のスプリットウィング ループにならって色づけしたものです。 [3]とまったく同じです。 ですから、スプリットウィングループは全体として1回ねじられているのです。 それでは、[3]から[4]への操作で、いったい何がどうなったのでしようか。
[7]: そのタネ明かしは、こうです。
[2]から始めます。 黄色い辺acを緑色の辺bdの上に重ねます。 これはスプリットウィング ループの捻じれを解いたものになっています。 つまり、ただのシリンダーと同じです。
上に乗っている辺acを含んだ面を矢印のように裏返します。 そして、辺acと辺bdを貼り合わせると、[4]が得られます。 つまり、[3]から[4]への過程では、いったん捻じれをキャセルして、それから改めて捻たわけです。 (*)のところは、継ないでも継ながなくてもかまいません。
[8]: 辺acと辺bdをずらせて重ね、隅cの付近を貼り合わせて一重にしたものです。 この場合、スプリットウィング ループの捻じれは解かれていません。 ですから、こうしても表裏の別はないのです。 矢印のように辿っていけば、それがわかります。
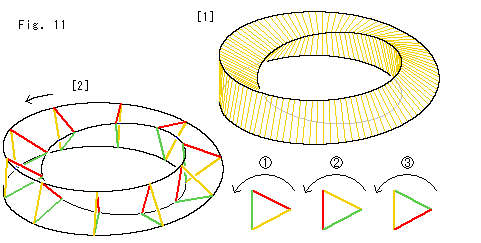
メビウスの帯はソリッドトーラスをねじり切りするとできるので、そのねじり角を変えた例を見てみます。
Fig.11をご覧ください。
[1]: ひねった三角柱ともいわれているもので、1つの面が捻じられてできています。 面は1つですが、空洞が形成されています。 その稜線は1本です。 メビウスの帯に似ていますけれども、そうではありません。 空洞の内側と外側が面の表裏になっています。 内側を裏とすると、見えるのは表側だけです。 面の一方の側だけが見えるために、メビウスの帯に似た感じを受けるのです。
[2]: ループの断面は正三角形になっています。 この正三角形は、ループを1周するごとに,,のように120ずつ回転して、3周するともとに戻ります。
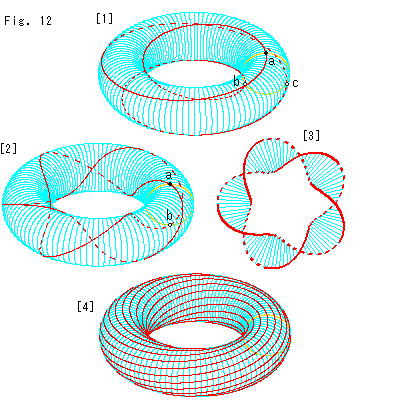Fig.12をご覧ください。
[1]: ソリッドトーラス上で、ひねった三角柱の頂点がどうなっているか見てみたものです。 赤い曲線は、そのときのトーラス面上の軌跡で、ループを3周しています。 点線は見えない側の様子です。 黄色いかすんだ円はトーラスのチューブの断面です。 その円周上の黒いスポットaと2つの
印しは、正三角形の頂点をなしています。 黒いスポットaをスタートポイントとしてみます。 すると赤い曲線は、1周したとき左下の点bを通り、2周めには右下の点cを通ります。 そして3周したとき、スタートとポイントaに帰ります。 このループの面は、1周ごとに120捻じれているわけです。
赤い曲線は、3周してチューブを1巻きしています。 3周1巻きとよんでおきます。 このよび方でいえば、一番簡単なメビウスの帯は2周1巻きです。
[2]: こころみに、トーラスのチューブをちょうど5回まわってル−プを1周してみたものです。 2周5巻きです。
2周めに入るとき、スタートポイントの真下の印しの点bを通ります。 ですから、前半の軌跡と後半の軌跡をチューブの直径でむすんでいけば、5回(180 x 5)ねじったメビウスの帯が得られます。
[3]:
[2]から切り出したメビウスの帯を真上から見たものです。 点線は、トーラスであったときにチューブの陰になっていたところです。
[4]:
メビウスの帯は巾にかぎりがあるので不便です。 そこで、面が1周して180ねじれているトーラスは如何でしようか。 赤い線はそのねじれ具合を表現しています。 これだと都合がよいように思えます。 しかし、なによりも、トーラスの面には表裏があります。 いくら捻じっても変わらないのです。 チューブの内側から見る場合があることもわすれてはなりません。
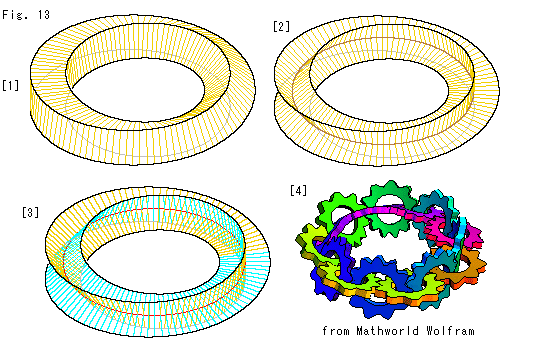Fig.13をご覧ください。
[1]: 1周して90捻じられているもので、断面は正方形です。 ひねった四角柱とよんでもよいでしよう。
[2]: これも1周して90捻じられているものですが、1周めと2周めの面と面が直交していていて、断面が十字形になっています。 しかし、縁の黒い線の形状は[1]とまったく同じです。 そして2周すると、180捻じれて継がります。 でも、こんなものをメビウスの帯とよんでよいのかどうか、迷いますね。
[3]: [2]を見やすく描きなおしたものです。 2周めの色を変え、下側を透けて見えるようにしています。
[4]: 歯車が[2]の面に沿って連なっています。 WebのMathworldのMobiusからコピーしたものですが、必見ですよ。 歯車が動いています。 捩れれた面とは、こんな機能をもったものかと感動します。
また、動くメビウスの帯が、Mobius animationにあります。 エッシャーの絵にメビウスの帯の上を蟻が這っているのがありますが、その蟻たちが実際に動いているのが、RUBAN DE MOBIUSにあります。
さて、メビウスの帯に関係することはまだまだありますが、ひとまず射影幾何にもどって進むことにしましよう。
[前章] [次章] [目次]