第３部 射影幾何から双曲幾何へ
Ch.39 射影幾何 (2) 
射影幾何をつづけましよう。 2次曲線を見ていきます。
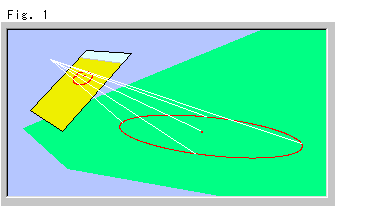
Fig.1は、地面の円の射影です。
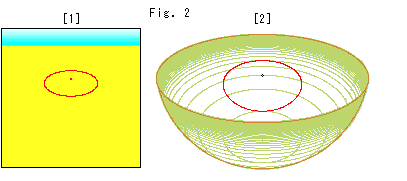
Fig.2をご覧ください。
[1]は、パネルスクリーンに射影された地面の円です。 地面の円が、だ円に見えています。
[2]は、地面に置いた半球面に射影された円です。
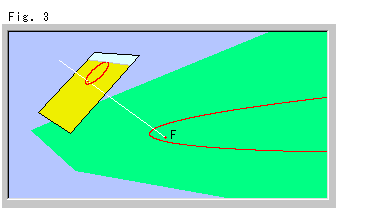
Fig.3は、地面の放物線の射影です。 白い射影線は、焦点Fのものです。 (他の射線は省いています｡)
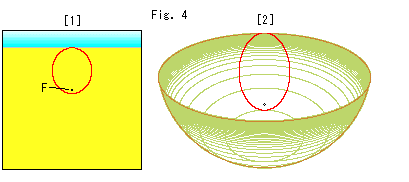
Fig. 4をご覧ください。
[1]は、パネルスクリーンに射影された放物線です。 これも、だ円のようなループに見えています。
[2]は、地面に置いた半球面に射影された放物線です。
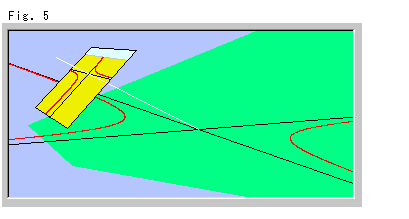
Fig.5は、地面の双曲線の射影です。 黒い直線は、漸近線です。
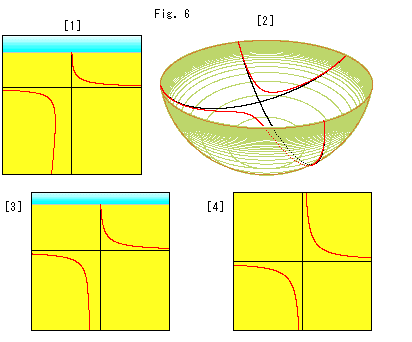
Fig.6をご覧ください。
[1]は、パネルスクリーンに射影された双曲線です。 その一つの枝は、無限遠直線上で漸近線と接しています。 下の方へ伸びている枝が漸近線から離れていくように見えています。 平行線の場合も、下へいくほど広がっていくように見えていましたね。
[2]は、地面に置いた半球面に射影された双曲線です。
[3]は、射影の中心(カメラ)をFig.4の右へ少しずらせて、双曲線の中心へ向けたときのパネルスクリーンの絵です。 下の方の枝が、漸近線から離れるのではなく、近づいていっています。
[4]は、射影の中心を地面の双曲線の中心の真上に置いたときの絵です。 当然、ふつうの双曲線です。
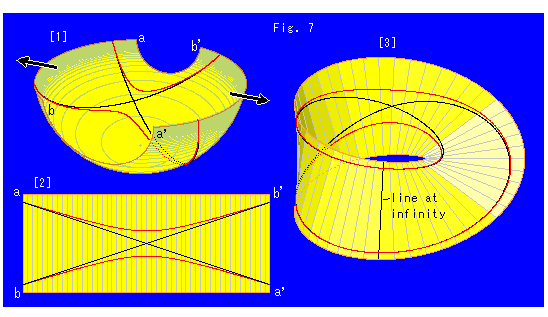
上のFig.7は、メビウスの帯の上で双曲線全体を見ようとするものです。 メビウスの帯は、射影平面の部分です。
[1]: Fig.6の半球面を図のように真っ直ぐに切ります。
[2]: それを矢印の方向に無理に広げて、帯状にします。
[3]: [2]の左右の一方を半捻りしてaとa'、bとb'をつなぎます。 すると、[1]の双曲線が乗ったメビウスの帯が得られます。 つなぎ目が無限遠直線(line at infinity)です。 赤い2本の双曲線が、無限遠直線のところで継ながって二重巻きの1つのループになっています。 そして、黒い漸近線は、それぞれでループになって、無限遠直線のところで双曲線と重なっています。
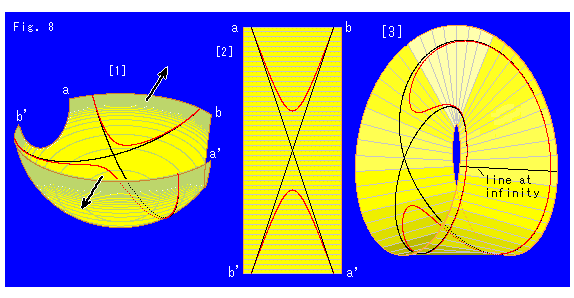
Fig.8もメビウスの帯の上で双曲線全体を見ようとするものです。 双曲線はFig.7のと同じですが、半球面の切り方を変えています。
[1]: こんどは半球面を図のように切ります。
[2]: それをFig.7の[2]と同様に広げます。
[3]: Fig.7の[3]と同様に上下の端を半捻りして継なぎ、メビウスの帯にします。 双曲線が、こんどは二重巻きにはならないで、1つのループになっています。 これは、メビウスの帯が射影平面全体ではないからです。
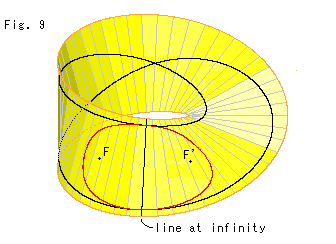
Fig.9は、焦点F,F'を描き込んだ双曲線です。 双曲線の中心から焦点までの距離を大きくとって、双曲線全体を見やすくしています。
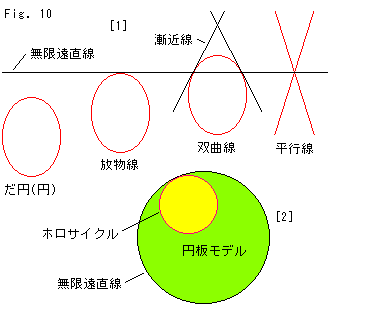
Fig.10をご覧下さい。
[1]は、無限遠直線のあたりの様子を観念的に描いたものです。 射影平面上では、2次曲線はみな同じです。 ただし、だ円(円を含む)は無限遠直線から離れており、放物線は無限遠直線に接触していて、双曲線は無限遠直線と交わっています。 そして、平行線は、無限遠直線のところで交わっています。
無限遠直線の両側(図の上の方と下の方)は、ともに有限の領域です。 この無限遠直線をまたぐことはできますが、無限遠を越えるものではありません。 そして、無限遠直線は、半球面の縁でもあるのですが、直線です。
[2]は、未だまとまっていない中途半端な考えですが、つぎのように捉えてみたものです。 円板モデルの縁も、(人工製品の)無限遠直線にほかならないといえますね。 そうだとすると、[1]に描かれている放物線の状況は、あのホロサイクルと同じということになります。 そして、ホロサイクルは閉じたループだとしてよいと思えます。 ただし、この円板モデルの面を射影平面だとしての話です。 円板の縁をFig.4の半球面の縁に対応するものだとすると、円板の対心点(直径の両端)を同一視すべきことになりますが、それは不都合ですね。 また、[1]では無限遠直線を横切れますが、円板モデルでは、それはできません。
ここで考え方を少し変えてみましよう。
平行線は与えられた点Pで交わるとします。 そうすると、無限遠直線がその点Pを通ります。 いいかえると、私たちは無限遠直線をどこにでも自由に引くことができます。 ただし、平行線はその無限遠直線上で交わらなければなりません。 この見方からすると、Fig.10は、2次曲線と平行線がしたがわねばならない規約を示しています。
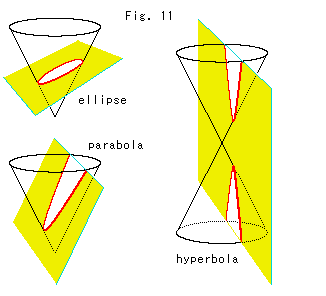
Fig.11は、よく見かける図です。 円錐を平面で切ると、すべての2次曲線が得られます。 これは、2次曲線はなにか統一さるべきものであることを示唆しています。 Fig.10の[1]が、その結果だといえるでしよう。 正直いって、円錐を切っている平面が、表裏のないものと考えられることなど思ってもみませんでした。 いや、そうだとしてよいかどうか、まだ決め手は見つかりません。
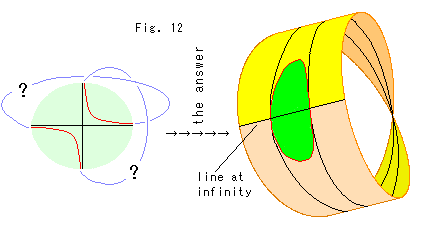
Fig.12は、双曲線の枝の先はどうなっているのかという疑問に答える一つのイラストです。 これは、しいて描いたもので、無論こんな風になっているのだと主張するものではありません。 捻れている向こう側をミステリゾーンだとしておいてもよいでしよう。 半球面の対心点を同一視することを素直に受け入れるなら、メビウスの帯はいりません。 つまり、射影平面は心で想うべきものです。
[前章] [次章] [目次]