第3部 射影幾何から双曲幾何へ
Ch.40 クロスキャップ (1) 
 メビウスの帯では、射影平面全体の様子を見ることがどうしてもできません。 ところが、それを可能にするクロスキャップ(crosscap)とよばれているモデルがあります。 どんなものか見てみましよう。
メビウスの帯では、射影平面全体の様子を見ることがどうしてもできません。 ところが、それを可能にするクロスキャップ(crosscap)とよばれているモデルがあります。 どんなものか見てみましよう。
メビウスの帯に円板で蓋をすればクロスキャップになるといわれています。 本当でしよいか?
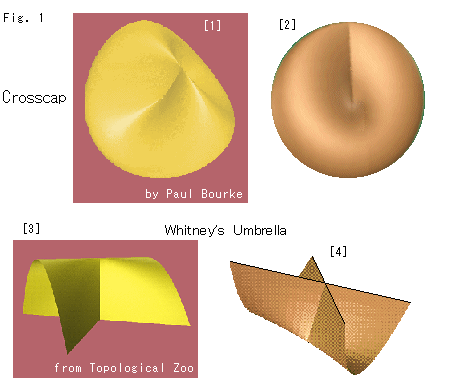
Fig.1をご覧ください。
[1]: クロスキャップはこんな格好の曲面です。 ポールブルケの作品で、Surfacesからとりました。 ぼた餅をお箸で挟むと、こんな形になります。 空気の少し抜けたゴムボールをつまんでみてもよいでしよう。 射影"平面"といっておきながら曲面をもち出しているわけですが、いうまでもなく、その曲面は平面とみなす約束のものです。 そして、メビウスの帯と同様に表裏がありません。
[2]: 窪んだところを正面にしたものです。
[3]: ホワイト二ーの傘(Whiteney's Umbrella)とよばれているもので、クロスキャップの上端のところの様子です。 トポロジーの動物園からとったものです。 こんな傘を二人でさすと、よいかもしれませんね。
[4]: [3]を逆さにしたものです。 Teoria de Singularidadesからとったものです。 このように、面が自分自身と交わっていることを自己交差しているといいます。
まず、クロスキャップを作る手順を追います。 そして、メビウスの帯とどのように似ているか違っているかを見ていくことにします。
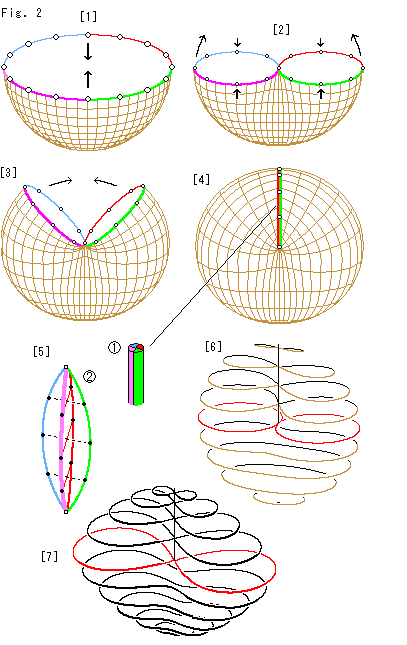
Fig.2をご覧ください。
[1]: 半球の縁を赤、青、ピンク、緑で色づけしてあるように4等分して考えます。 縁に並んでいる丸印しは、無数にある対心点を代表しています。 半球はゴム製だとして、矢印のように向こう側とこちら側の一組の対心点をつなぎます。
[2]: 一組の対心点をくっつけたところです。 こうしておいて、前後を絞りながら左右の縁を合わすように引き伸ばしていきます。
[3]: 左右の縁を引き伸ばしている途中です。 すべての対心点を一致させるために、赤とピンクのころとを接合させ、青と緑のころとを接合させようとしています。
[4]: 半球の縁をしぼって線分にしてしまったところです。 この線分を自己交差の交線(Line of Self-intersection)とよんでおきます。 そこでは、赤・青・ピンク・緑の4つの線分が折りたたまれたようになっています。 こうして半球面が縁のない閉じた曲面に変わり、クロスキャップが出来上がりました。
[5]: 自己交差の交線は のように4本の線分が特別な重なり方をしてできています。
のように4本の線分が特別な重なり方をしてできています。  は、これをを強いて4つにほぐしたものです。 赤とピンク、青と緑が対になって、それぞれ別個に同一視されています。 対をむすんでいる点線は、その同一視を表現してたものです。 上端と下端だけは、4本が1点になっています。 この自己交差の交線が射影平面の無限遠直線です。 ただし、ここでの無限遠直線はループを折りたたんだものになっています。
は、これをを強いて4つにほぐしたものです。 赤とピンク、青と緑が対になって、それぞれ別個に同一視されています。 対をむすんでいる点線は、その同一視を表現してたものです。 上端と下端だけは、4本が1点になっています。 この自己交差の交線が射影平面の無限遠直線です。 ただし、ここでの無限遠直線はループを折りたたんだものになっています。
[6]: 完成したクロスキャップを水平に切って斜めから見たものです。 赤い断面は自己交差の交線の下端で切った断面です。 そこから上の断面は8の字形です。
[7]: クロスキャップをつくるのに半球を使ったのは、これまでの経緯によったからです。 半球にその下に広がった平面を中心射影して、半球の縁を無限遠直線だとしました。 そして、半球の縁が無限遠直線であるためには、縁にある対心点が同一視されなければならない。 といったことから、半球によったわけです。
しかし、形を作るだけなら、[6]に似たものを描くことは簡単です。 8字形の曲線の式を利用すればよいのですから。 図はその一例で、カッシニの卵形の公式をアレンジして描いたものです。 こんなのに面を張っても、クロスキャップが得られます。
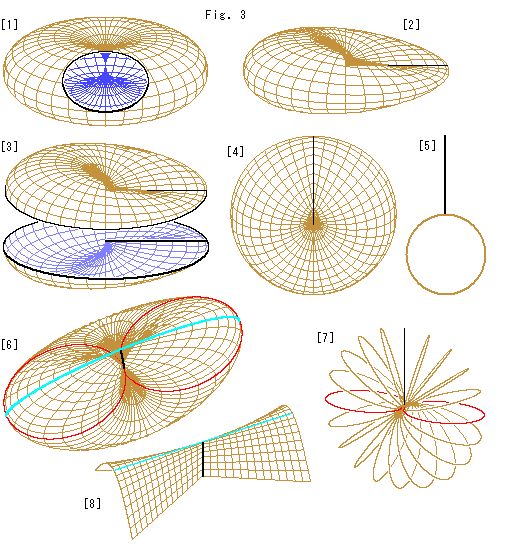 Fig.3をご覧ください。
Fig.3をご覧ください。
穴の詰ったトーラスからクロスキャップをつくります。 穴の詰ったトーラスは、ふつうのト−ラスのチューブを膨らましても、球の1組の対心点を突き合わせてもできます。
[1]: 穴の詰ったトーラスの内部を覗けるようにしたものです。 中央の1点で継ながっています。
[2]: 一箇所を図のように挟んで、直線状にします。 そこが自己交差の交線です。 もうこれで、クロスキャップの形ができ上がりました。
[3]: [2]を上下に切って、内部を見たものです。
[4]: [2]を立てて、こちらえ向けたものです。 上端がわずかに凹んで見えるのは、こちら側へちょっと傾けて描いてあるからです。 格子の目は、[1]に対応させているので、Fig.2のとは異なっています。
[5]: [4]を画面に垂直切った断面です。
[6]:大きくして、斜め上から見たところです。 水色の線は尾根で、赤い線は中心を通る水平な面で切ったところです。 黒い自己交差の交線が短く見えるのは、中心から下の方が[5]のように膨らんでいるからです。
[7]: 放射状に切っていった断面です。 赤い線は、自己交差の交線の下端での断面です。 一番下のは円で、それより上が楕円です。 だ円の短軸は、上へいくほど小さくなり、一番上で自己交差の交線になっています。
[8]: クロスキャップの上端の狭い範囲は、ホワイト二ーの傘にして描くことができます。 水色の線は傘の尾根で、少しも曲がっていません。 それより向こうが見えるために、[4]の上端がちょっと凹んでいるように見えるのです。
こうしてクロスキャップができましたが、この格子は座標として半球面上の点を写すことはできません。 それは曲面の性質が半球面とは異質だからです。 しかし、そのことには立ち入らないでおきます。 そして、格子は立体感を出す模様だとしておきます。 メビウスの帯と同様に、クロスキャップの形もゴム製品のように変形してもよいのですから。
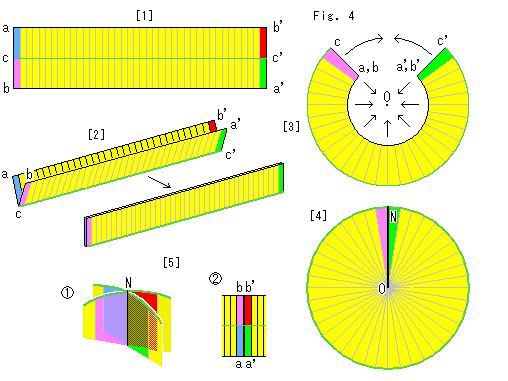 Fig.4をご覧ください。
Fig.4をご覧ください。
メビウスの帯をつるのに親しんでいる短冊からクロスキャップをつくります。
[1]: ふつうの短冊ですが、端を4つに色分けしています。 緑色の線cc'はセンターラインです。
[2]: センターラインで二つ折りにします。
[3]: 二つ折りにした短冊を緑色のセンターラインcc'を外側にして、図のようにまるく曲げ、その内側を1点Oへ絞っていきます。
[4]: すると、円板になります。 円板といっても、その向こう側の面とこちら側の面は短冊のセンターラインを挟んでいたものなので、押さえつけた袋状になっています。 黒い半径NOは曲げた短冊の継ぎ目です。 その継ぎ目NOを1つの線分にして、クロスキャップの自己交差の交線にします。
[5]: 自己交差の交線の上端Nの左右を裂いて覗くと、 のようになっています。 自己交差の交線上だけを見れば、
のようになっています。 自己交差の交線上だけを見れば、 のように、180
のように、180 捻じた短冊の両端をつき合わせたのと同じ状態です。 つまり、[4]の線状の継ぎ目(自己交差の交線)NOは、曲げた短冊を一瞬にして180
捻じた短冊の両端をつき合わせたのと同じ状態です。 つまり、[4]の線状の継ぎ目(自己交差の交線)NOは、曲げた短冊を一瞬にして180 捻じるところであるわけです。
捻じるところであるわけです。
この円板を自己交差の交線をそのままにして膨らませば、クロスキャップの形になります。 しかし、本当のクロスキャップではありません。 クロスキャップは四方八方をカバーするものですが、短冊の上下の側線ab',ba'は1点Oになってしまっているので、その外側といったものは円板上にはありません。 ですから、膨らませたものは、本当のクロスキャップからその一部を欠いたものです。
けれども、短冊の巾を十分大きくとっておいて、欠いたところの点Oを避けるか、短冊の巾を無限大だと見立てれば使えます。 すると、逆に円板はクロスキャップを押さえつけて、平坦にしたものだとみることができます。 実際、この円板はたいていの場合に役立ちます。 それで、こうして作った円板を平坦なクロスキャップと名づけておくことにます。
**************************************************
それではクロスキャップの性質を探っていきます。
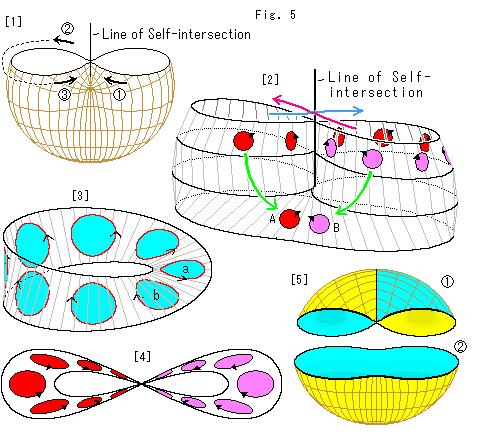 Fig.5をご覧ください。
Fig.5をご覧ください。
[1]: クロスキャップを自己交差の交線があるところで水平に切って、その上部を取り除いたものです。 右手前の から自己交差の交線を横切ると、矢印
から自己交差の交線を横切ると、矢印 のように左の向こう側へと進みます。 つづけて点線のように進むと、こちら側の
のように左の向こう側へと進みます。 つづけて点線のように進むと、こちら側の に来ます。 ここで矢印
に来ます。 ここで矢印 と
と を見くらべると、向きが逆になっています。
を見くらべると、向きが逆になっています。
[2]: 自己交差の交線の下端を挟んで水平に切り出しました。 縦縞の線は、4つある水平な断面線を同じキザミ数で等分したところをむすんだもので、観察用の目安です。 [1]の格子線とはちがいます。
まず、上の方に並んでいる矢印つきの円板を見てください。 左の方から青い矢印のように自己交差の交線を横切って円板を動かします。 円板はぐるっと回って、右の方からこちら側へ戻ってくると、裏返っていて、円周の向きが逆になっています。 そのまま進めて、もういちど自己交差の交線を赤い矢印のように横切り、[1]の から
から のようにして元のところにもどると、円板ははじめの姿になります。 メビウスの帯上で円板を2周させたときと同じです。 赤と青の矢印は立体交差しているのではありません。 一瞬共有点を通ることがあっても、まったく別個に動くことを表現しているのです。
のようにして元のところにもどると、円板ははじめの姿になります。 メビウスの帯上で円板を2周させたときと同じです。 赤と青の矢印は立体交差しているのではありません。 一瞬共有点を通ることがあっても、まったく別個に動くことを表現しているのです。
下の方のAとBは、もとの円板と自己交差の交線を1度だけ横切ってきた円板です。 同じ面の上に円板の表と裏が共存できるのです!
[3]: メビウスの帯と比べてみます。 水色の円板aが、1周して戻ってきて円板bになっています。 これで見ると、円板bは裏返って面の反対側にきています。 メビウスの帯に表裏はありませんが、部分ぶぶんでいえば、一方の側と他方の側を区別していうことができます。 しかし、表裏の有無にかかわらず1つの面ですから、どちら側という必要がなければ、区別しなくてもよいわけですね。 すると、[2]と同様にメビウスの帯の上でも円板の表と裏が共存していることになります。 つまり、クロスキャップ上での動きとメビウスの帯上での動きは、まったく同じです。
クロスキャップも、メビウスの帯と同様に、その面の上だけでの動きがゆるされています。 そして、単側とかどうとかいう前に、もとから1つの面です。
[4]: [2]の円板が並んでいるところを水平に切り出したものです。 左側では円板の表ばかしが見え、右側ではその裏ばかしが見えています。 メビウスの帯では1周すると、面の反対側にきます。 クロスキャップで面の反対側といえば、空洞になっている内側を指すことになりますが、内外は考えにいれないのです。 左側を一周すると右側へ行き、右側を一周すると左側へと8の字形のコースをたどります。 ですから、この[4]の左右はメビウスの帯の1周めと2周めに対応しています。
[5]: クロスキャップを自己交差の交線がある上の方と、それがない下の方に分けて、色を塗ってみます。 わざと面の内外を区別していきます。 すると、上側 では、自己交差の交線を境に表面と内部の色が入れ替わります。 下側
では、自己交差の交線を境に表面と内部の色が入れ替わります。 下側 では、そのようなことはありません。 これでは、全体を塗ることができません。
では、そのようなことはありません。 これでは、全体を塗ることができません。
表裏を区別したために、こうなってしまったのですね。 表裏を区別しないことにするのはよいのですが、いったいどこでどう区別がなくなっているのでしようか? 自己交差の交線に仕掛けがあるにちがいありません。 どこかで表裏の区別がなくなるのではありません。 クロスキャップ全体が、もとから表裏を区別していないのです。 表裏があるかないかを問わないのです。 メビウスの帯に表裏がないのとは、ちょっと違います。
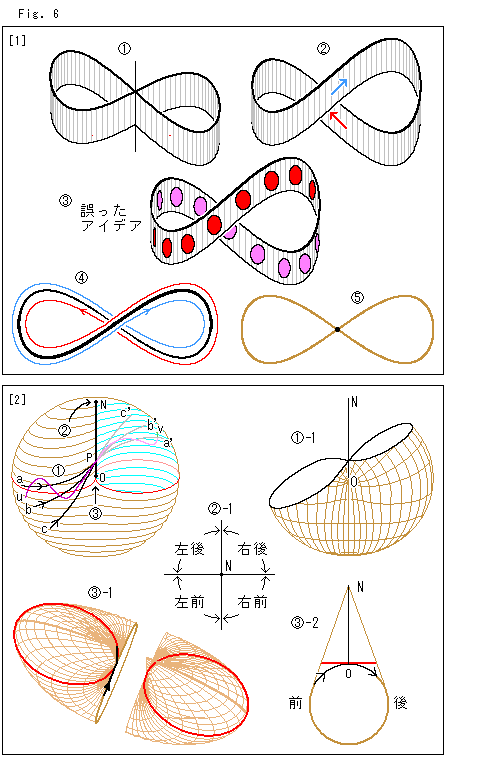 Fig.6をご覧ください。
Fig.6をご覧ください。
[1]: クロスキャップの断面が8の字形になっているところだけを見ます。
 : 自己交差の交線で面が交わっている様子です。 この交差点では、右折も左折も禁止されています。
: 自己交差の交線で面が交わっている様子です。 この交差点では、右折も左折も禁止されています。
 : ですから、自己交差しているところは、図のように上下に引き離されていると想ってもよいはずですね。
: ですから、自己交差しているところは、図のように上下に引き離されていると想ってもよいはずですね。
 : しかし、円板をこの上で動かしてみると、図のようになって、[4]と符合しません。 これは間違った考え(wong idea)です。
: しかし、円板をこの上で動かしてみると、図のようになって、[4]と符合しません。 これは間違った考え(wong idea)です。
 : 真上から
: 真上から を見たものです。 この赤や青の線のように、内側と外側を出たり入ったりすると想うのも誤りです。
を見たものです。 この赤や青の線のように、内側と外側を出たり入ったりすると想うのも誤りです。
 : 自己交差の交線を横切るときの動き方をきっちり定めるには、面の表裏を区別しないことにすればよいのですね。 なんどもいいますが、表裏を区別しないというのは、表裏の有無にかかわらず、表裏を区別しないということです。 まだ表裏がないことをしっかりとはつかめていません。 それで、便宜的に、クロスキャップを物理的に閉じた面だとして、穴でも開けないかぎり空洞内へ入ることはできないと考えておきます。 意図的にするのは自己交差の交線における同一視だけです。 同一視というのは、自分と同じ者がそこにいるということで、たがいに移り合えることです。 鏡の中の自分のように、自分は自分ですから。 (後に出てくる紙細工の話も参照してください。)
: 自己交差の交線を横切るときの動き方をきっちり定めるには、面の表裏を区別しないことにすればよいのですね。 なんどもいいますが、表裏を区別しないというのは、表裏の有無にかかわらず、表裏を区別しないということです。 まだ表裏がないことをしっかりとはつかめていません。 それで、便宜的に、クロスキャップを物理的に閉じた面だとして、穴でも開けないかぎり空洞内へ入ることはできないと考えておきます。 意図的にするのは自己交差の交線における同一視だけです。 同一視というのは、自分と同じ者がそこにいるということで、たがいに移り合えることです。 鏡の中の自分のように、自分は自分ですから。 (後に出てくる紙細工の話も参照してください。)
[2]: 上ではっきりしたのは、自己交差の交線をちゃんと横切るときです。 そうではない場合は、どうでしようか。
 : クロスキャップに輪切り状に水平なスライスラインを入れて、自己交差の交線NOから右のこちら側を剥いだものです。 赤いスライスラインは、自己交差の交線NOの下端Oを通っています。
: クロスキャップに輪切り状に水平なスライスラインを入れて、自己交差の交線NOから右のこちら側を剥いだものです。 赤いスライスラインは、自己交差の交線NOの下端Oを通っています。
いま左下から右上の方へa,b,cのように真直ぐに自己交差の交線NO上の点Pへ向かって進みます。 点Pへ来ると、そこから先は向こう側へ移り、aはa'へ、bはb'へ, cはc'へと進んでいきます。 ジグザグに u-P-v と紫色の線のように歩んで行っても、同様です。 どんなに斜めに自己交差の交線NOを渡っても問題ありません。
 -1は、自己交差の交線NOを平面で斜めに切った切口です。 左右が対称ではありませんが、やはり8字形になっています。
-1は、自己交差の交線NOを平面で斜めに切った切口です。 左右が対称ではありませんが、やはり8字形になっています。
 : 左のこちら側から出発して、自己交差の交線NOの上端Nへ来たとします。 そこでは、8字形の断面が1点になってしまっています。 そも、断面というものがありません。 1点である上端Nには向こう側とこちら側の別はありません。 どちらへも進めないのでしようか。 自己交差の交線NO上では上端Nにかぎらず、向こう側とこちら側がくっついているところですから、両者を区別できないのです。 はて、区別できないところで右や左といわれても、どうしようもないではありませんか。 巧い考えがあります。 といっても、いままで無自覚にやっていたことです。
: 左のこちら側から出発して、自己交差の交線NOの上端Nへ来たとします。 そこでは、8字形の断面が1点になってしまっています。 そも、断面というものがありません。 1点である上端Nには向こう側とこちら側の別はありません。 どちらへも進めないのでしようか。 自己交差の交線NO上では上端Nにかぎらず、向こう側とこちら側がくっついているところですから、両者を区別できないのです。 はて、区別できないところで右や左といわれても、どうしようもないではありませんか。 巧い考えがあります。 といっても、いままで無自覚にやっていたことです。  -1のように方位として向こう側とこちら側を区別すればよいのです。
-1のように方位として向こう側とこちら側を区別すればよいのです。
 : こちら側の面で自己交差の交線NOの真下から上へときて、その下端Oに着いたとします。 さて、どちらへ進んだらよいのでしようか。 左から来たのなら右向こう側へ行けばよいし、右から来たのなら左向こう側へ行けばよいのですが、来たのは左からでもなく右ちらでもないのですから、同一視すべき相手が定まりません。 自己交差の交線NOの上を歩めば、同一視の相手の点を勝手に選ぶことになってしまいます。
: こちら側の面で自己交差の交線NOの真下から上へときて、その下端Oに着いたとします。 さて、どちらへ進んだらよいのでしようか。 左から来たのなら右向こう側へ行けばよいし、右から来たのなら左向こう側へ行けばよいのですが、来たのは左からでもなく右ちらでもないのですから、同一視すべき相手が定まりません。 自己交差の交線NOの上を歩めば、同一視の相手の点を勝手に選ぶことになってしまいます。
ですから、
自己交差の交線上は通行止め
としておかねばなりません。
クロスキャップを左右のちょうど真中で垂直に切って、上の方から覗いてみると、 -1のようになっています。 赤いループは、自己交差の交線NOの下端Oを通る水平断面です。 左側に自己交差の交線とその下の切口を添えています。 左側のクロスキャップを真直ぐに立てて、真横から見ると、
-1のようになっています。 赤いループは、自己交差の交線NOの下端Oを通る水平断面です。 左側に自己交差の交線とその下の切口を添えています。 左側のクロスキャップを真直ぐに立てて、真横から見ると、 -2のようになっています。 左右をえらばずに進むとすれば、このように点Oから向こう側の真下へ行くことになります。 そして、点Oを通過して向こう側に入ってしまえば、あとは自由です。 もっとも、この下端Oは点ですから、実際上は、自己交差の交線上でないところなら、どこへでも向かって行けます。
-2のようになっています。 左右をえらばずに進むとすれば、このように点Oから向こう側の真下へ行くことになります。 そして、点Oを通過して向こう側に入ってしまえば、あとは自由です。 もっとも、この下端Oは点ですから、実際上は、自己交差の交線上でないところなら、どこへでも向かって行けます。
これで、すっかりクロスキャップ上の動き方がきまりました。
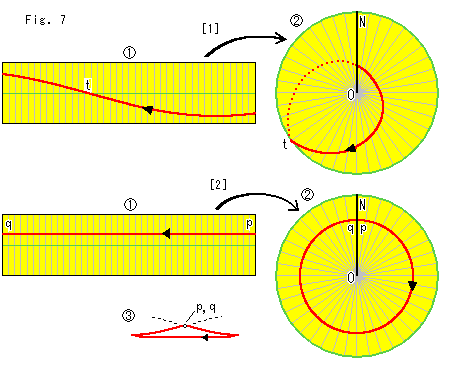
Fig.7をご覧ください。
短冊上の曲線を平坦なクロスキャップ上で見てみます。
[1]:  の赤い曲線は、半球面上の大円を短冊に移したものです。 赤い曲線の流れを観察しやすいように黒い三角矢印をつけています。 緑色の線はセンターラインです。 赤い曲線が点tでセンターラインを横切っています。 この赤い曲線を平坦なクロスキャップ上にうつすと、
の赤い曲線は、半球面上の大円を短冊に移したものです。 赤い曲線の流れを観察しやすいように黒い三角矢印をつけています。 緑色の線はセンターラインです。 赤い曲線が点tでセンターラインを横切っています。 この赤い曲線を平坦なクロスキャップ上にうつすと、 のように円周の点tのところで向こう側(円板の裏側)へ行き、自己交差の交線NOのところでこちら側へ抜けて戻り、ループになっています。
のように円周の点tのところで向こう側(円板の裏側)へ行き、自己交差の交線NOのところでこちら側へ抜けて戻り、ループになっています。
[2]: こんどは、短冊 上にセンターラインに平行な赤い線pqを引きます。 その赤い線pqは、平坦なクロスキャップ
上にセンターラインに平行な赤い線pqを引きます。 その赤い線pqは、平坦なクロスキャップ 上では円のようになって見えます。 でも、本当の円ではありません。 端点pも端点qも、同じこちら側の面の上にあります。 しかし、その面は自己交差の交線NOを通って向こう側へ続いているので、点pのあるところと点qのあるところは、直接には継がっていません。 点pと点qは同じ場所にあっても、継ながってはいないのです。 端点pが同一視する相手は端点qではなく、端点qが同一視の相手は端点pではないからです。
上では円のようになって見えます。 でも、本当の円ではありません。 端点pも端点qも、同じこちら側の面の上にあります。 しかし、その面は自己交差の交線NOを通って向こう側へ続いているので、点pのあるところと点qのあるところは、直接には継がっていません。 点pと点qは同じ場所にあっても、継ながってはいないのです。 端点pが同一視する相手は端点qではなく、端点qが同一視の相手は端点pではないからです。  は、そこを誇張して、
は、そこを誇張して、 の上から見たものです。 これは、膨らんだ本当のクロスキャップでも同じです。
の上から見たものです。 これは、膨らんだ本当のクロスキャップでも同じです。
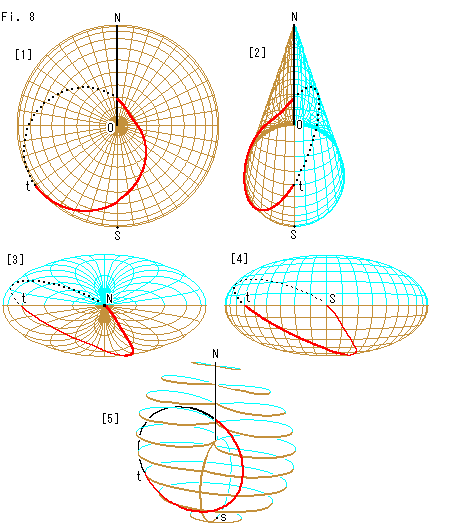
Fig.8をご覧ください。
[1]: クロスキャップを真正面に向けたところです。 赤い曲線はFig.7の[1]と同じものですが、膨らんだ正しいクロスキャップをつかっているので、角ばらずに滑らかになっています。 点tは、曲線がこちら側から向こう側へ回り込んでくるところです。
[2]: 真横から見たものです。 水色のところが[1]の背面です。
[3]: 北極Nから見下ろしたものです。 (格子線の数は減らしています。)
[4]: 南極Sから見上げたものです。
[5]: 斜めから見た曲線です。 ループになっています。 半球面上の大円は、円ではなくて半円です。 それが、メビウスの帯上と同様に、クロスキャップ上でも1つのループになるのです。
クロスキャップ上に曲線を描くことは、後の[クロスキャップ(3)]でいろいろやってみます。 それは残しておいて、ここでは先ず、クロスキャップそのものを見ていきます。
**************************************************
クロスキャップ(射影平面)は、メビウスの帯とそれにかぶせる円板に分解できるといわれています。 どのようにしてそういえるのかを追ってみます。
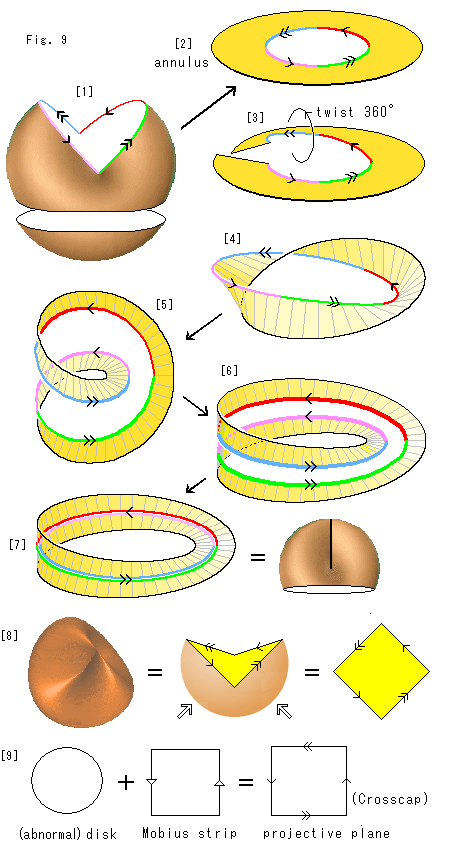 Fig.9をご覧ください。
Fig.9をご覧ください。
[1]: クロスキャップの自己交差の交線を裂いて、図のように開きます。 その切口を色づけして、向きを含めて同一視される縁に矢印をつけます。 そして、自己交差の交線より下の方で上下に二分します。
このような矢印のついた図は二様に解釈されます。
(a) 一つは、矢印の通りに同一視が実行されてあるものとする。 [1]でいえば、切口の開いた図であるけれども、切口が閉じられいるのと同じだとして見るのです。
(b) もう一つは、同一視を実行するときは矢印のようにするという約束だけを表しているものとする。 [1]でいえば、ものは見えている通りで、同一視の実行はされていないものとして見るのです。
ところが、どんな本でも、(a)と(b)のどちらを指しているのかを一々いっていません。 しかしここでは、はっきりさせておきましよう。 [1]は、(b)の解釈で見てください。 これから同一視の実行をしていくのです。
[2]: クロスキャップの上部を平たく広げて、穴あき円板にします。 穴が開いていて同心円の円板状に変形し得るものは、よくアニュラス(annulus)とよばれています。 図の円板もアニュラスです。
[3]: アニュラスを切って、360 捻り(twist)ます。
捻り(twist)ます。
[4]: 捻ったものを、継ぎなおしたところです。
[5]: 細長くして捻じれをならし、内側に輪をつくったところです。
[6]: 輪と輪の間を狭めていくと、メビウスの帯をその形のままででセンターラインで切ったものになります。
[7]: [6]の隙間を閉じて、同一視する線をくっつけます。 赤とピンク、青と緑の線がそれぞれぴったりとくっついて、完了します。 これは、もとのクロスキャップの上部と同じです。 ただし、メビウスの帯の縁は捻じられていますが、クロスキャップの上部のすそは、そうではありません。 同じというのは、連続的に1対1の対応がつくということです。 等号はそれを意味しています。
[8]: 一方、クロスキャップ全体は、[1]でいった(a)の見方をすることで、自己交差の交線を裂いて矢印をつけたものでも表現できます。 それを外から押しつけて平たくすると、クロスキャップを矢印をつけた四角形で表せます。 矢印付き四角形は、トポロジーの本でよく見かけるもので、矢印の向きを合わせて辺を同一視するものです。 その同一視が物理的に実行できるかどうかは問いません。 ここでは、抽象的な同一視が実行されてあるものとして見てください。
[9]: 射影平面(projective plane)であるところのクロスキャップ(モデル)が、メビウスの帯(Mobius strip)と円板の貼り合わせたものであることを表したものです。 左辺の円は、[1]で二分したクロスキャップの下部を円板に変形したものです。 メビウスの帯も矢印付き四角形で表しています。 プラス記号は抽象的に貼り合わすことです。
円板は、クロスキャップの下部としてなら、ふつうの円板でよいのですが、メビウスの帯と貼り合わせるとなると、その周がメビウスの帯の縁と一致していなければなりません。 捻じれていないもの(円板)と捻じれているもの(メビウスの帯)を継ぎ合わせることは、絶対にできない相談ですね。 ですから、この円板は異常(abnormal)なシロモノです。 そして、そこは抽象的にということで済ませておきます。
クロスキャップの上部の裾と、[7]でのメビウスの帯の縁とについてはどうでしようか。 前者はふつうのループですが、後者は両端を継げたコイル状です。 けれども、いまは、それも同じだと想ってください。 どちらがどちらに同じなのかと問うこともしないでください。 抽象的な算法です。
クロスキャップを表している[9]の右辺の四角形には、メビウスの帯の四角形の矢印のないところにも矢印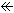 が入っています。 ですから、クロスキャップは、その矢印付き四角形で見ても、四方八方をカバーしているのです。 左右が捻じて継ながれ、上下も捻じて継ながれていることになってます。
が入っています。 ですから、クロスキャップは、その矢印付き四角形で見ても、四方八方をカバーしているのです。 左右が捻じて継ながれ、上下も捻じて継ながれていることになってます。
よく「射影平面の四角形の辺の貼り合わせを物理的に実行することは不可能である」といわれます。 しかし、自己交差を許せば可能です。 自己交差を必要当然なことと考えれば、実行したものがクロスキャップだということになります。 ただ、惜しいことに、クロスキャップはモデルであり、それを平面としてみなければなりません。 感覚的に平面とみなすことは、さほどの負担にはなりません。 その面の上に住んっでいると想えばよいのですから。 しかし、具体的に図を描いて考えようとすると、とても困難ですね。
それにしても、[3]でアニュラスを切っているところが気になりますね。 [2]は物理的な表裏のあるものですから、そのままではどんなにいじくっても、メビウスの帯に変形することはできません。 そのために、一旦切断するわけですが、いかにも意図的ではありませんか。
もう一つ気になることがあります。 クロスキャップから円板を取り去った残りがメビウスの帯になるのですが、無傷のクロスキャップをメビウスの帯と同じものだといいたい気持ちがします。 そういうためには、切り取るべき円板のところを例外域だとしておかなければなりません。 その例外をなくすことはできませんが、円板を十分小さくして、そこだけを避けていくことにすればよいでしよう。 円板を小さくするといっても、1点にしてしまうことはできません。 点と円は異なるものですから。 さいわい、取り去る円板は自己交差の交線から外れたとろなら、どこでもよいのです。
それなら、便利な特異点ということばをつかってみましよう。 例外域がそれです。 すると、円板を切り取らなくても、「クロスキャップは、特異点を除いてメビウスの帯である」といえるではありませんか。
いや、まってください。 それは、射影平面のことを考えていないときの話です。 クロスキャップは射影平面全体をカバーしますが、メビウスの帯ではそうはいきません。 ですから、やはりメビウスの帯は、クロスキャップの一部をなしているというのが正解です。
上のFig.9のことは正しいにしても、話しが早すぎますね。 同じことですけれど、射影平面であるところの対心点を同一視した半球面から出発してみましよう。
Fig.10をご覧ください。
[1]: 半球面を上下に切ります。 上部は はアニュラスです。 その上縁の前後左右を色分けして、三角矢印しをつけます。 そして、こちら側をF、向こう側をRとラベルをつけておきます。
はアニュラスです。 その上縁の前後左右を色分けして、三角矢印しをつけます。 そして、こちら側をF、向こう側をRとラベルをつけておきます。
[2]: RとFを分離して、それぞれの左右に矢印をつけておきます。
[3]: RとFを平たくして長方形にします。
[4]: Rを(裏返さずに)回転して、RとFの色のついた辺を貼りあわせます。 長方形の左右の矢印が上下逆になっているので、両端を捻じて継ないで、メビウスの帯をつくります。 これで半球面の上部の同一視が完了しました。
この長方形は、半球面の内側と外側を隣り合わせにしたものになっています。 注目しておくべきことですね。 (前章までで半球面から切り出した短冊と、ここでの長方形は異なったものです。)
[5]: 残しておいた半球面の下の方は、前と同様に円板で表します。 メビウスの帯も、矢印つき四角形で表現します。 そして、この四角形に円板を(抽象的に)当てたものが、対心点を同一視した後(after identification)の半球面(=射影平面=クロスキャップ)だというわけです。 Fig.10でメビウスの帯を作ったのとは、ずいぶんやり方が違いますが、結果はまったく同じです。
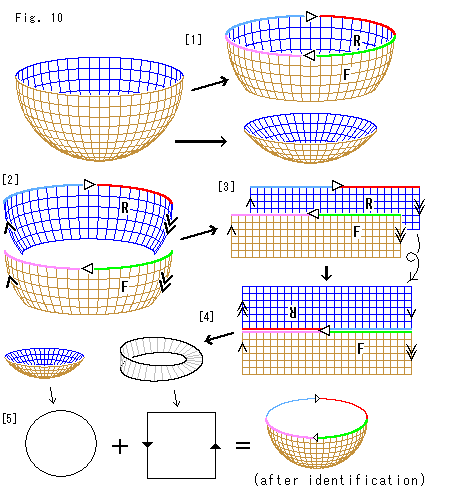
 Fig.11をご覧ください。
Fig.11をご覧ください。
面を切って継いだりするようなことをトポロジーでのことばで手術とよんでいます。 私たちが扱う範囲での手術のことをちょっと整理しておきます。 (クラインの壷とよばれるもののように、自分自身を貫通するようなものは、考えていません。)
[1]: 黄色い曲面を赤い線でA,Bに切る(cut)とします。
[2]: 切った端([1]の赤い境界線)は、AにあればBにはない。 逆にBにあれば、Aにはがない。 なぜなら、1つの点が2箇所に存在することはあり得ないのだから。 というのが、ふつうの数学的な考え方ですね。 デデキントの切断とかいうやつです。 日常生活でも、挟みで二つに切った布の切れ目の糸くずの一つ一つが、床に落ちることはあっても、二つになった布の両方にあるといったことはありません。
[3]: しかし、2本の赤い線のように、切られたAとBの両方に端があるというのが、トポロジーでの考え方です。 1つのものが2つになったのではなく、同じものが両方にあるのです。 つまり、AとBの切れ目は、分かれていても、同一視しするのです。 この考えによれば、切られていても、継がっているのと同じだとしてもよいのです。 継ぎもどすのも、同一視の実行ということで自然です。 デデキントの切断もトポロジーでの考え方も公理だといわれています。 手術は、このトポロジーの考え方によっています。
[4]: 例として、メビウスの帯を手術します。
 : メビウスの帯のこちら側の見えている面に、上下左右表裏の見分けやすい文字FとRを書いておきます。 向こう側に矢印
: メビウスの帯のこちら側の見えている面に、上下左右表裏の見分けやすい文字FとRを書いておきます。 向こう側に矢印 を入れておきます。
を入れておきます。
 : メビウスの帯を矢印
: メビウスの帯を矢印 で切って、捩れをといて、短冊にに広げます。 文字FとRの間に赤い線を適当にひきます。
で切って、捩れをといて、短冊にに広げます。 文字FとRの間に赤い線を適当にひきます。
 : 赤い線で切り離します。 ここまでが、切ったというところです。 これから新しく同一視をしていきます。
: 赤い線で切り離します。 ここまでが、切ったというところです。 これから新しく同一視をしていきます。
 : 面Rを裏返して、矢印
: 面Rを裏返して、矢印 ,
, の同一視を実行します。 いまはメビウスの帯ではなく表裏があるので、濃淡をつけて描いてあります。 透けて見える文字Rは、上下が逆になっています。
の同一視を実行します。 いまはメビウスの帯ではなく表裏があるので、濃淡をつけて描いてあります。 透けて見える文字Rは、上下が逆になっています。
 : 右端を固定して、左端を回転矢印tの方向(左から見て右回り)に、180
: 右端を固定して、左端を回転矢印tの方向(左から見て右回り)に、180 捻じます。
捻じます。
 : 両端をこちら側へ曲げて、赤い線を向かい合わせたところです。 まだ赤い線の同一視は実行されていなくて、曲げた短冊のままですので、表裏の濃淡をつけたままです。 よく見ると、この同一視をしても、もとのメビウスの帯とまったく同じものになってしまいます。
: 両端をこちら側へ曲げて、赤い線を向かい合わせたところです。 まだ赤い線の同一視は実行されていなくて、曲げた短冊のままですので、表裏の濃淡をつけたままです。 よく見ると、この同一視をしても、もとのメビウスの帯とまったく同じものになってしまいます。
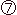 : それではと、向こう側へ曲げてみました。 ところがまたも、もとのメビウスの帯と同じものになるではありませんか。 実は、短冊をつくったときの逆手順をふんでいたのです。 新しいものを得るには、
: それではと、向こう側へ曲げてみました。 ところがまたも、もとのメビウスの帯と同じものになるではありませんか。 実は、短冊をつくったときの逆手順をふんでいたのです。 新しいものを得るには、 で180
で180 よりもっと捻じる(180
よりもっと捻じる(180 の奇数倍)か、捻じる方向を逆にしなければなりません。
の奇数倍)か、捻じる方向を逆にしなければなりません。
もっとも、自分自身や他のものに絡ませてから赤い線の同一視をするなら、捻じる方向を問わず、変わったものが得られます。 しかし、どのようにして同一視しても、見る観点によっては、何も変わっていないことになります。
手術は完了しなければならないのです。 途中でおいたのでは、手術をしたことにはなりません。 手術の完了は、すべての同一視をすませることです。 しかし、その同一視に抽象的なものも含めることにすれば、どの段階でも手術完了とみなすことができます。 ですから、切りっぱなしに見えるものでも、抽象的な同一視を実行して眺めれば、手術は終わっていることになります。 (2箇所でメビウスの帯を切りましたが、新しいタイプのメビウスの帯を得るためだけなら、1箇所切ればたります。 2箇所も切ったのは、たんに説明の便でした。)
この例で記憶しておくべきことは、手術の途中で同一視のパートナーの一方を裏返していることです。 その裏返しは、部分としてそうであって、広域に(あるいは手術の進んだあとで)見れば、捻じることと同じだということです。 手術が完了したときには、表裏のないものに戻ってしまうのですから。
さらに大事なことは、この例の手術では捻り方の違うメビウスの帯を得ることができるのですが、それは元のメビウスの帯と本質的には何も変わっていないということです。 つまり、手術をしても、再度同一視をするのだから、見た目に変わったものができても、面の性質や機能に変化はないのです。 もちろん、それは抽象的に同一視する場合も含めてのことです。 どんな手術をしても、メビウスの帯が円筒に化けたりすることは絶対にありません。
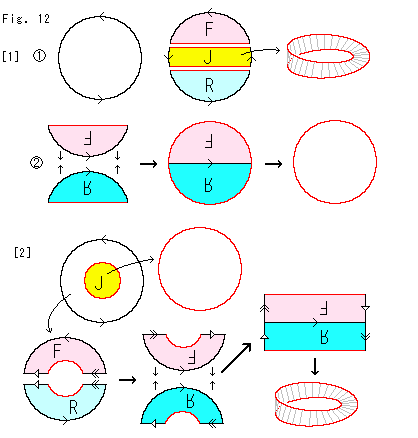
Fig.12をご覧ください。
対心点が同一視されている円板で射影平面を表現して、射影平面の分割を見てみます。
[1]: 円板を三つ切りにします。
 : 中央のJは、そのままメビウスの帯になります。
: 中央のJは、そのままメビウスの帯になります。
 : Fを裏返さずに回して上下を逆にします。 Rは、裏返して上下を逆にしてFの下におきます。 矢印
: Fを裏返さずに回して上下を逆にします。 Rは、裏返して上下を逆にしてFの下におきます。 矢印 のついた黒い線をつき合わせて同一視をおこないます。 そして、赤い線を上下のまげると、円板になります。 これは、ふつうの円板です。
のついた黒い線をつき合わせて同一視をおこないます。 そして、赤い線を上下のまげると、円板になります。 これは、ふつうの円板です。
[2]: こんどは、黒い射影平面の円板の内部をくり抜いて、そのまま円板にします。 これも、ふつうの円板です。 残ったアニュラスを2つに切って、[1]と同じ要領で矢印 のついた黒い線の同一視をします。 すると短冊になり、メビウスの帯が得られるます。
のついた黒い線の同一視をします。 すると短冊になり、メビウスの帯が得られるます。
ここで注目されるは、[1]と[2]では射影平面である円板の切り方がまったく違うのに、同じ結果だということです。
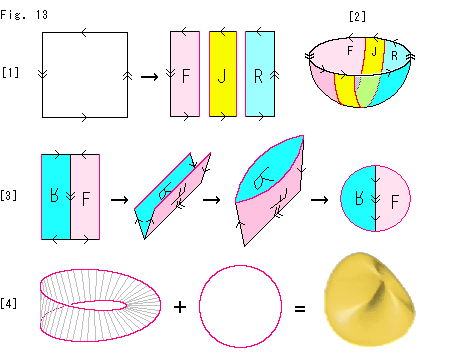 Fig.13をご覧ください。
Fig.13をご覧ください。
矢印つき四角形をつかって、射影平面の分割を見てみます。 ここでは、主に円板が手術を受けることになります。
[1]: 射影平面の四角形を3つに切って、それぞれにラベルF,J,Rを書き込んでおきます。
[2]: このカットが半球面から短冊を切り出すときのカットに対応していることの参考図です。
[3]: まず、RとFをとります。 Rを裏返して、Fと貼り合わせます。 ついで、図のように折って、上下も貼り合わせます。 すると、ボートのような格好のものができます。 それを押し広げて形をととのえると、円板が得られます。
[4]: つぎに、[1]のJの上下を貼り合わせると、メビウスの帯ができます。 円板の直径にある矢印は、同一視が完了しているので省きます。 そして、メビウスの帯に抽象的に円板をかぶせれば、もとのクロスキャップ(射影平面)が得られるというわけです。 ここでも、左辺の2項の縁がともに赤い線であることに注目してください。
**************************************************
オイラー数(オイラー標数)とのかかわりを見てみます。
一般にいわれているオイラー数を曲面別にリストにしてみると、

となっています。
オイラー数が同じでも、同じ曲面とはかぎりません。 曲面が捩れているかどうかは、オイラー数では区別できないのです。 その区別は、三角形分割の辺につけられる同一視の矢印で判断します。 このような不便はありますが、オイラー数は絶大な力を発揮します。 どんなに曲面をいじくっても、オイラー数は変わらないのです(トポロジー不変量)。 そのことを覚えおいて、見ていきます。
 Fig.14をご覧ください。
Fig.14をご覧ください。
まず、クロスキャップのオイラー数を求めます。
[1]: モデルそのままで三角形分割します。 黒い線は自己交差の交線です。 水色の線は、自己交差の交線と尾根を通る平面との交線です。 赤い線は、水色の線に直交した平面との交線です。 ただし、上は自己交差の交線の下端を通っています。 簡単のために、これらを三角形分割の辺にします。
[2]: 自己交差の交線を裂いて、それが4本の線の同一視されたものからなることを示したものです。 自己交差の交線の上下の端は、共有点になっています。
[3]: 4つの三角形に分けてみたところです。 3つの角が直角だという歪んだ三角形です。
[4]: 三角形を整形して、自己交差の交線以外の共有辺を継いだところです。 これで、頂点v、辺e、面fをしっかり数えることができます。 同一視されているものは1つに数えるので、vは3、eは6、fは4となります。 そして、オイラー数 は
は
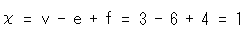 と算出されます。
と算出されます。
[5]: [4]から内部の頂点と4つの辺を取り除くと、射影平面の標準的な四角形の四隅に同一視される点の印しをいれたものになります。 その同一視の印しを三角形分割の頂点として数え、[4]と比べると、頂点が1つ、辺が4つ、面が3つ少なくなっていますが、
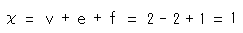 となって、オイラー数
となって、オイラー数 が1であることに変わりはありません。
が1であることに変わりはありません。
ここで、ちょっと注意が必要です。 この標準的な四角形の四隅の印しは、図の上では3辺の共有点ではありません。 けれども、その四角形の同一視を実行してクロスキャップというモデルにしたときの三角形分割の頂点になるものです。
さいわいにも、たいていの場合、矢印つきの三角形や四角形でそれらの頂点を三角形分割の頂点と同じだとしてうまくいきます。 なぜ巧くいくのかは詮索しないで、ともかく進めましよう。 そして、不都合に出くわしたときに考えることにします。
[6]: 射影平面のオイラー数が1であることは、簡単に見出せます。 ふつうの球面のオイラー数が2であることは、よく知られていので、それを利用します。 球面のすべての対心点が同一視されているとすると、その球面は射影平面のモデルになります。 球面のv,e,fの数は、ふつうの球面を同様に三角形分割したもののちょうど半分です。 ですから、射影平面のオイラー数は2の半分、つまり1です。
もし、球面でなく内部の詰った球体と考えるなら、射影空間のモデルということになりますが、いまは表面だけに注目しています。
[7]: 対心点が同一視されている球面を赤道で切って、半球面にします。 その半球面のオイラー数は、もとの球面と同じです。 なぜなら、縁(赤道)を除いた半球面上の点には同一視のパートナーがいないので、v,e,fの数が変わらないからです。
ですから、半球面のオイラー数は1であり、その半球面を変形したクロスキャップのオイラー数も1であるというわけです。
半球面のオイラー数を直接得ることもできます。 半球面を上から見て[5]の四角形とくらべると、両者はトポロジー的に同じものですから、[5]と同様にv,e,fを数えればよいわけです。
[8]: クロスキャップのオイラー数を直接得ようとする場合でも、実際の三角形分割をしなくてすみます。 図のようにv,e,fを数えれば、即座に  = 2 - 2 + 1 = 1 とつかめます。 [5]と同様です。
= 2 - 2 + 1 = 1 とつかめます。 [5]と同様です。
[9]: メビウスの帯のオイラー数 はどうでしようか。
はどうでしようか。
メビウスの帯を三角形分割すると、v = 3, e = 7, f = 4 ですから、
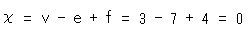 です。
です。
矢印つき四角形(短冊)の内部から[5]と同様に頂点と4つの辺を取り除くと、
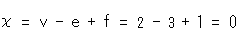 となります。 メビウスの帯でも、矢印つき四角形からオイラー数が得られました。
となります。 メビウスの帯でも、矢印つき四角形からオイラー数が得られました。
オイラー数が0なので、むろんメビウスの帯は射影平面ではありません。 (オイラー数が0だとユークリッド幾何をもつといわれていますが、それにはかかわらないでおきます。)
さらにオイラー数を追っていくのですが、その前に、クロスキャップ(射影平面)の分割を四角形の切り方を変えたもう一つの方法で見ておきます。
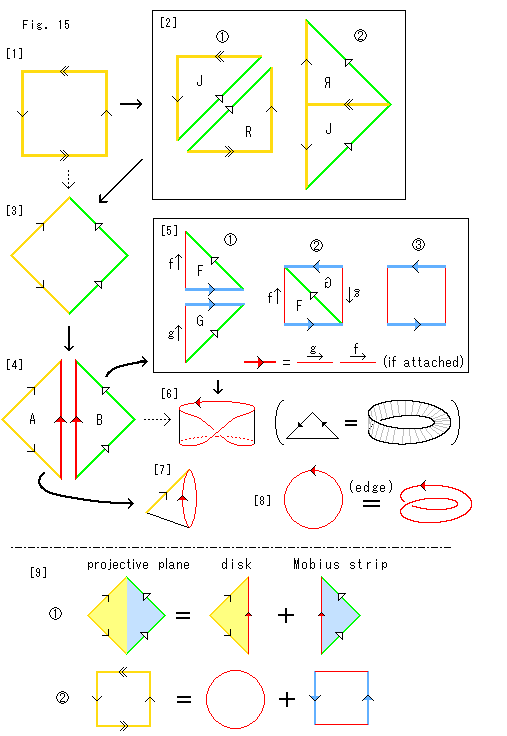 Fig.15をご覧ください。
Fig.15をご覧ください。
[1]: クロスキャップ(射影平面)の標準的な四角形です。
[2]: その四角形を都合のよいものに変えます。
 : 対角線で切って2つに分け、ラベルJ,Rをつけます。 新しい緑色の辺に三角矢印をつけておきます。
: 対角線で切って2つに分け、ラベルJ,Rをつけます。 新しい緑色の辺に三角矢印をつけておきます。
 : Rを裏返して、三角形Jの上に継なぎ、矢印
: Rを裏返して、三角形Jの上に継なぎ、矢印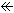 の同一視を実行します。
の同一視を実行します。
[3]: 矢印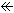 がついた線分は、同一視が完了したので省き、ひし形にします。 この四角形を閉曲面に描けるとよいのですが、自己交差をゆるしてもできせん。
がついた線分は、同一視が完了したので省き、ひし形にします。 この四角形を閉曲面に描けるとよいのですが、自己交差をゆるしてもできせん。
けれども、[1]を描き替えただけのものですから、[1]の代わりに用いることができます。 点線の矢印は、そのことを表しています。
これを出発点として、すすめます。
[4]: また対角線で切って、ラベルA,Bをつけます。 こんども新しい赤い辺に矢印をつけておきます。
[5]: まず三角形Bをとって、メビウスの帯の四角形(短冊)にします。
 : F,Gに切ります。 新しい辺に青い矢印をつけます。 赤い辺には、[3]の赤矢印ではなく、矢印f,gを辺のよこに添えておきます。 赤い辺の上に矢印ををつけると、三角形FとGの赤い辺が同一視さるべきものと表されてしまうからです。 三角形FとGの赤い辺は、三角形Bの赤い辺を分割した別個のものです。 つまり、矢印gの辺に矢印fの辺を同方向に継ぎ足したものが三角形Bの赤い辺であったのです。
: F,Gに切ります。 新しい辺に青い矢印をつけます。 赤い辺には、[3]の赤矢印ではなく、矢印f,gを辺のよこに添えておきます。 赤い辺の上に矢印ををつけると、三角形FとGの赤い辺が同一視さるべきものと表されてしまうからです。 三角形FとGの赤い辺は、三角形Bの赤い辺を分割した別個のものです。 つまり、矢印gの辺に矢印fの辺を同方向に継ぎ足したものが三角形Bの赤い辺であったのです。
 : Gを裏返してFに継ぎ、緑色の辺の同一視を実行します。
: Gを裏返してFに継ぎ、緑色の辺の同一視を実行します。
 : 同一視を完了した緑色の辺を省くと、メビウスの帯の四角形になります。 矢印f,gは添えていません。 それらがなくても、メビウスの帯にしたときに、赤い線は自動的に直列に継がれるからです。
: 同一視を完了した緑色の辺を省くと、メビウスの帯の四角形になります。 矢印f,gは添えていません。 それらがなくても、メビウスの帯にしたときに、赤い線は自動的に直列に継がれるからです。
[6]: [5]から得たメビウスの帯です。 その赤い線は、1つのループになっているので、赤い矢印をいれています。
囲み[5]は三角形Bからメビウスの帯を得る途中の操作です。 青い線は、そのときだけ出現しました。 ですから、この[5]をまるごと省いて点線のように、三角形Bをそのままメビウスの帯だとしてもよいのです。 つまり、括弧( )の中のように捉えるわけです。
[7]: 残しておいた三角形Aは、黄色い辺の同一視がすぐにできて、円錐状になります。 その頂点を底面へ押しつけ、同一視を完了した黄色の辺を省くと、円板になります。
[8]: かくて、円板の円周とメビウスの帯の縁(edge)が、ともに1つのループで、同じものであることがわかりました。
[9]: 射影平面の分割を矢印つきの三角形や四角形で表現します。
 : [3]と[4]をとって描いたものです。 各図形の内部も着色しています。 面としても成り立つからです。 これなら、抽象的な三角形ですけれども、そのままで分離結合ができます。
: [3]と[4]をとって描いたものです。 各図形の内部も着色しています。 面としても成り立つからです。 これなら、抽象的な三角形ですけれども、そのままで分離結合ができます。
 : 射影平面の標準的な四角形[1]を円板とメビウスの帯の四角形で表したものです。 左辺と同じ色の線は右辺にはありません。 各図形の内部は、もちろん面ですけれども、
: 射影平面の標準的な四角形[1]を円板とメビウスの帯の四角形で表したものです。 左辺と同じ色の線は右辺にはありません。 各図形の内部は、もちろん面ですけれども、 のように着色することはできません。 円板はふつうの円板です。 そしてメビウスの帯の縁は、上下の赤い線です。 それらの縁を、面と面が触れないで貼り合わせることは不可能です。
のように着色することはできません。 円板はふつうの円板です。 そしてメビウスの帯の縁は、上下の赤い線です。 それらの縁を、面と面が触れないで貼り合わせることは不可能です。  ,
, を相い補うものとして、見るべきですね。
を相い補うものとして、見るべきですね。
それでは、オイラー数にもどります。
射影平面の分割と結合の過程がオイラー数 とどう関わっているかを、矢印つき四角形などで見ていきます。
とどう関わっているかを、矢印つき四角形などで見ていきます。
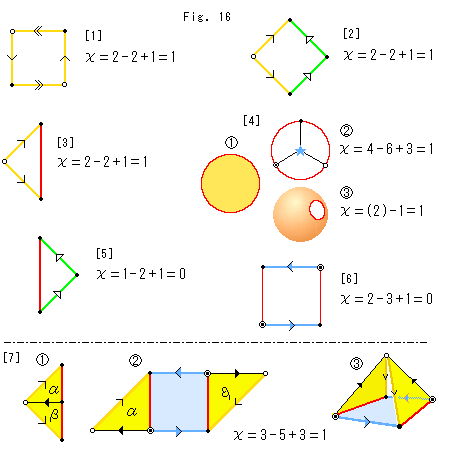 Fig.16をご覧ください。
Fig.16をご覧ください。
辺の端の印しは三角形分割の頂点としてあつかいます。 しかし、三角形分割をした上でつけるのではなく、辺の矢印に拠って区別しています。 そして、同じ印しの頂点は一つに数え、同じ矢印の辺も一つに数えるというルールにしたがっていきます。 すでに求めたものや描いたものも含めています。 Fig.15と見比べながら行ってください。
捩れがあってもオイラー数は変わりません。 捩れているかどうかは、辺の矢印で判断されます。
[1]: 射影平面(クロスキャップ)の標準的な四角形です。
[2]: 手術で[1]を変形したものです。 頂点 が1つ増え、頂点
が1つ増え、頂点 が1つ減っています。
が1つ減っています。
[3]: [2]の左半分です。
[4]: [3]を円板に変形したものです。
 : そのまま頂点は0、辺は1、面は1と数えると、0 - 1 + 1 = 0 となってしまいます。 変形してもオイラー数は変わらないのですから、ゼロではいけません。
: そのまま頂点は0、辺は1、面は1と数えると、0 - 1 + 1 = 0 となってしまいます。 変形してもオイラー数は変わらないのですから、ゼロではいけません。
三角形分割においては、
各面はトポロジー的な円板であり、各辺はトポロジー的な線分
でなければなりません。
 : 円周は線分ではないので、ちゃんと三角形分割をしてからv,e,fを数えたものです。
: 円周は線分ではないので、ちゃんと三角形分割をしてからv,e,fを数えたものです。
 : 円板は球面に穴が1つあるものとトポロジー的に同じです。 それは球面を三角形分割した面の1つが欠けたものです。 ですから、円板のオイラー数は、球面のオイラー数2から1を引けばよいのです。 結果は
: 円板は球面に穴が1つあるものとトポロジー的に同じです。 それは球面を三角形分割した面の1つが欠けたものです。 ですから、円板のオイラー数は、球面のオイラー数2から1を引けばよいのです。 結果は と変わりません。
と変わりません。
[5]: [2]の右半分です。
[6]: [5]をメビウスの帯にしたものです。
[7]: [3]と[6]を継いでみます。
 : [3]の上下を
: [3]の上下を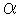 ,
,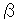 に分けます。
に分けます。
 : 三角形
: 三角形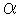 と
と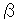 をメビウスの帯[6]の左右に貼り合わせたものです。 三角形
をメビウスの帯[6]の左右に貼り合わせたものです。 三角形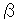 が裏返しになっています。
が裏返しになっています。
 : 頂点
: 頂点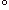 だけを同一視してみたものです。 二面の欠けた四角錐になっています。 この先、同一視をつづけていけばクロスキャップになるはずですが、描ききれません。
だけを同一視してみたものです。 二面の欠けた四角錐になっています。 この先、同一視をつづけていけばクロスキャップになるはずですが、描ききれません。
円板と一穴球面がトポロジー的に同じであるのは当然です。 その簡単なことが途中で役立ちました。 また、ピラミッドが出現しました。 これらには、なにか示唆するところがあるようですね。
 Fig.17をご覧ください。
Fig.17をご覧ください。
射影平面の正体は、「メビウスの帯に円板をかぶせたものだ」とか「球面の穴にメビウスの帯を貼ったものだ」といわれています。 しかし、この表現には、どこかひっかかりますね。
射影平面PのモデルであるクロスキャップAをB,Cに分割します。 Bを手術でメビウスの帯B'にし、Cを平坦な円板C'にします。 して、メビウスの帯B'と円板C'を抽象的に貼り合わせます。 さて、この B' + C' を射影平面Pの正体だというのです。 おかしいですね。 P(= A) = B + C であるからといって、B,CをB',C'に変えた後でも、P = B' + C' だといっているのです。
補いましよう。
"抽象的に"とは、もちろん、逆コースをたどることではありません。 ここでの"抽象的に"とは、P = B' + C' だと無理やりに空想することです。
円板C'はふつうの円板です。 けれども、それは単独でのときであって、メビウスの帯に貼り合わせるときには奇怪な振る舞いをするシロモノだと想っておきます。
射影平面をメビウスの帯と円板に分解することは、この後もあちこちで色々とやってみますので、ずっと読み進めてください(Ch.37まで)。 そうすれば、当然なことになってきます。
 Fig.18をご覧ください。
Fig.18をご覧ください。
上とは違った切り方で、伸縮性のあるクロスキャップを切ってみます。
 : クロスキャップを図のように切ります。 分断するのではなく、赤く染めた自己交差の交線のところは残しておきます。
: クロスキャップを図のように切ります。 分断するのではなく、赤く染めた自己交差の交線のところは残しておきます。
 : 切り口を上限に引き離したところです。 Oはクロスキャップの中心で、自己交差の交線の端点です。
: 切り口を上限に引き離したところです。 Oはクロスキャップの中心で、自己交差の交線の端点です。
 :
:  の向こう側をこちらへ向けたものです。
の向こう側をこちらへ向けたものです。
 : 切り口の縁と中心Oをむすぶ直線からなる螺旋面です。 この螺旋面は自己交差していますが、表裏があります。 この螺旋面は、切ったクロスキャップ
: 切り口の縁と中心Oをむすぶ直線からなる螺旋面です。 この螺旋面は自己交差していますが、表裏があります。 この螺旋面は、切ったクロスキャップ ,
, (=
(= )とトポロジー的に同じもの(同相)です。
)とトポロジー的に同じもの(同相)です。
ふつうの切ってないクロスキャップでは、自己交差の交線を通過してから、自己交差の交線を通過する前の点へ直接行くことができます。 しかし、ここにある切ったものでは、それができません。 そのために、表裏のあるものになったのです。
[前章] [次章] [目次]
 メビウスの帯では、射影平面全体の様子を見ることがどうしてもできません。 ところが、それを可能にするクロスキャップ(crosscap)とよばれているモデルがあります。 どんなものか見てみましよう。
メビウスの帯では、射影平面全体の様子を見ることがどうしてもできません。 ところが、それを可能にするクロスキャップ(crosscap)とよばれているモデルがあります。 どんなものか見てみましよう。
 Fig.3をご覧ください。
Fig.3をご覧ください。 Fig.4をご覧ください。
Fig.4をご覧ください。 Fig.5をご覧ください。
Fig.5をご覧ください。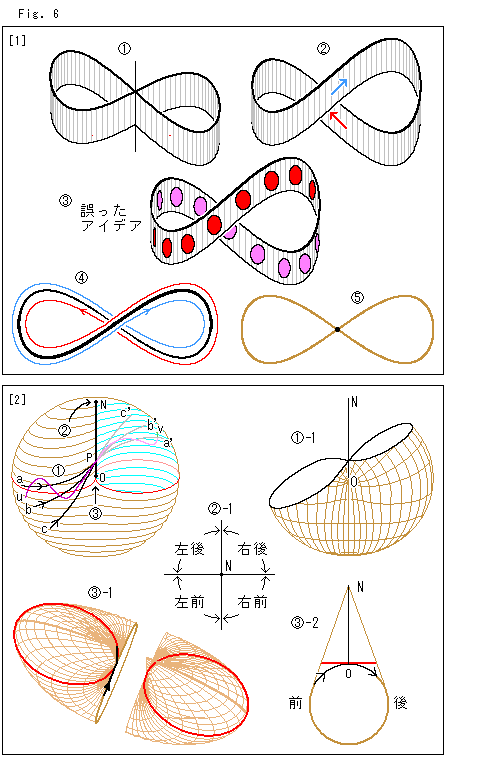 Fig.6をご覧ください。
Fig.6をご覧ください。

 Fig.9をご覧ください。
Fig.9をご覧ください。
 Fig.11をご覧ください。
Fig.11をご覧ください。
 Fig.13をご覧ください。
Fig.13をご覧ください。
 Fig.14をご覧ください。
Fig.14をご覧ください。 Fig.15をご覧ください。
Fig.15をご覧ください。 Fig.16をご覧ください。
Fig.16をご覧ください。 Fig.17をご覧ください。
Fig.17をご覧ください。 Fig.18をご覧ください。
Fig.18をご覧ください。